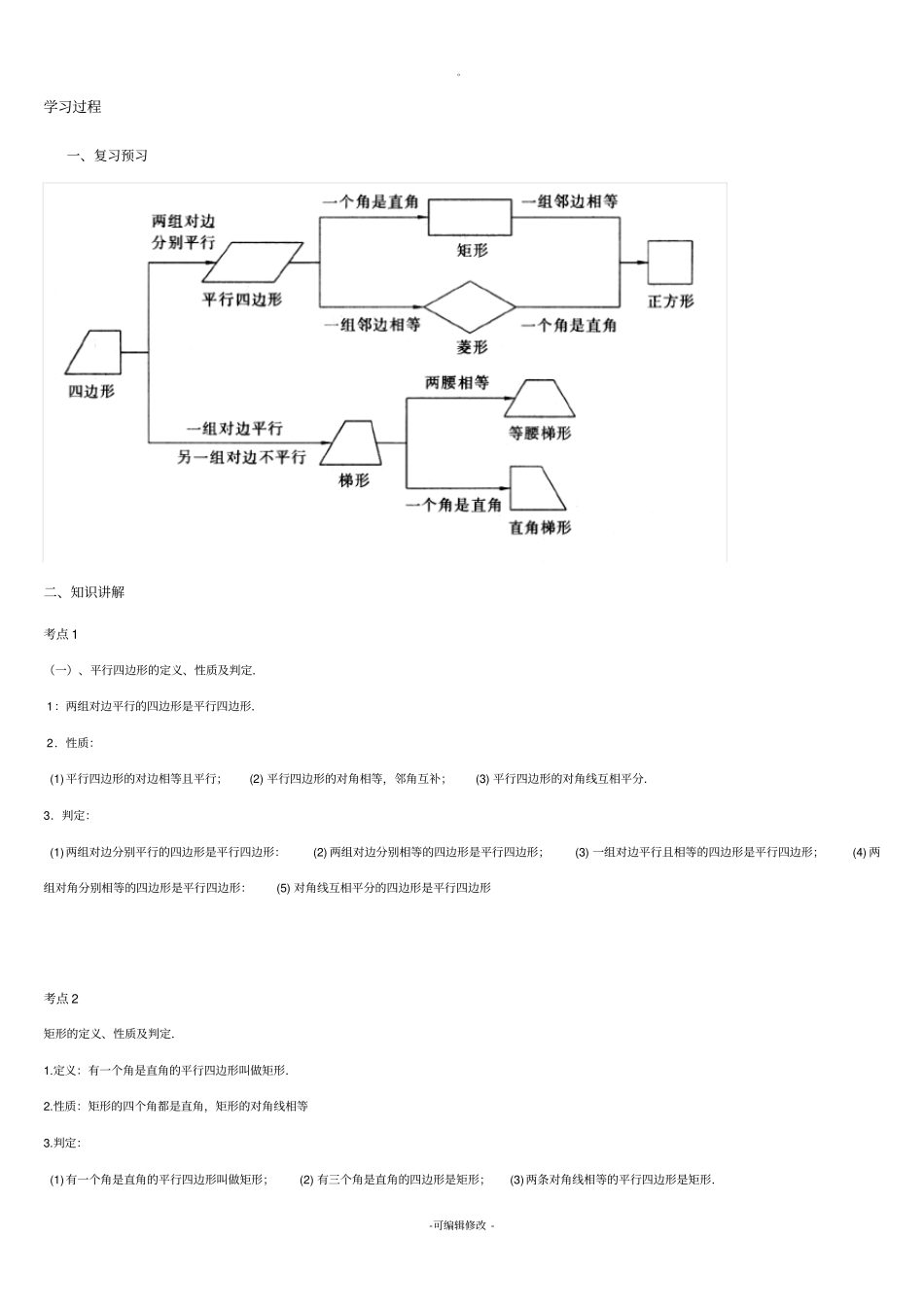
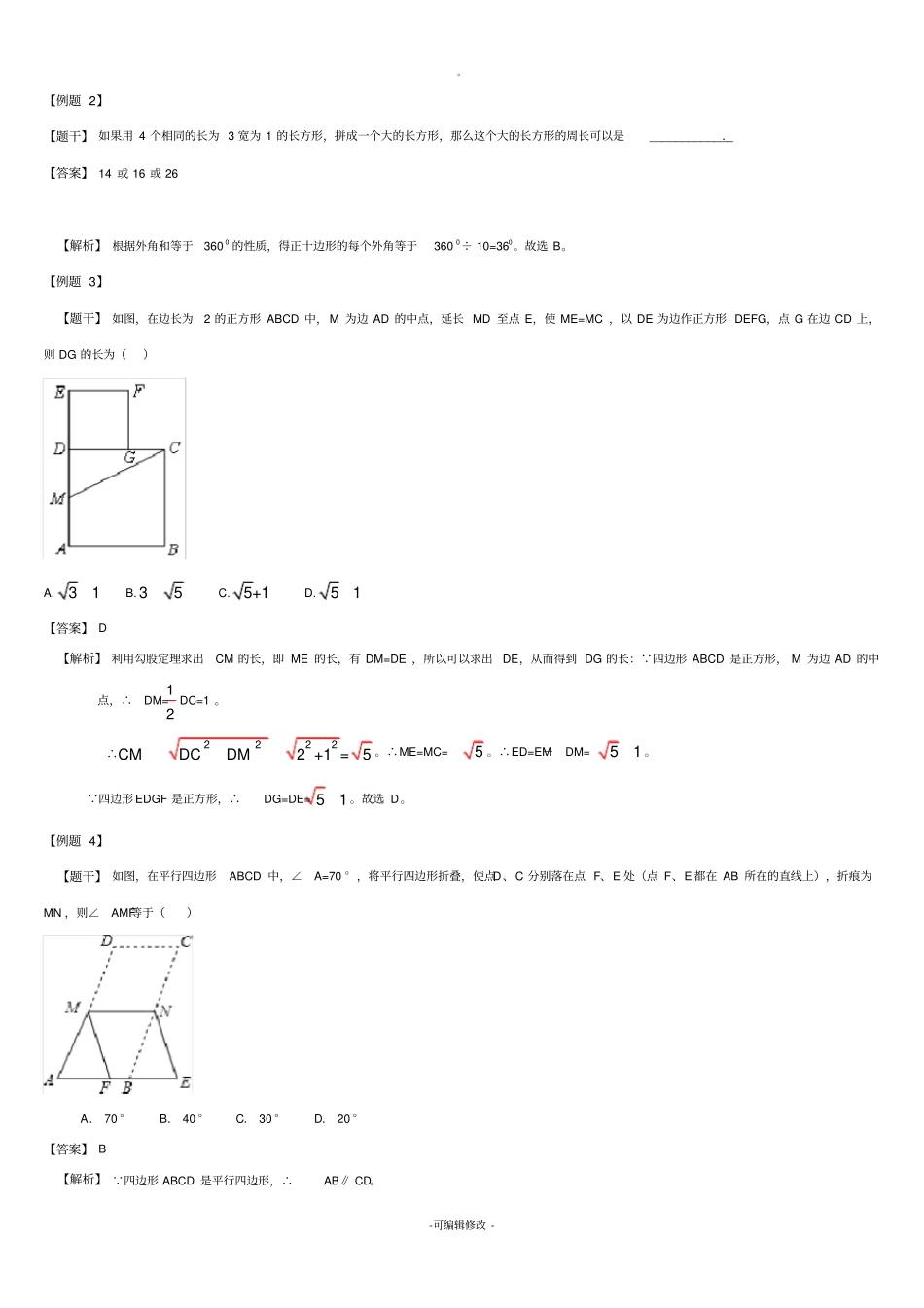
。-可编辑修改-学习过程一、复习预习二、知识讲解考点1(一)、平行四边形的定义、性质及判定.1:两组对边平行的四边形是平行四边形.2.性质:(1)平行四边形的对边相等且平行;(2)平行四边形的对角相等,邻角互补;(3)平行四边形的对角线互相平分.3.判定:(1)两组对边分别平行的四边形是平行四边形:(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形:(5)对角线互相平分的四边形是平行四边形考点2矩形的定义、性质及判定.1.定义:有一个角是直角的平行四边形叫做矩形.2.性质:矩形的四个角都是直角,矩形的对角线相等3.判定:(1)有一个角是直角的平行四边形叫做矩形;(2)有三个角是直角的四边形是矩形;(3)两条对角线相等的平行四边形是矩形.。-可编辑修改-4.对称性:矩形是轴对称图形也是中心对称图形.考点3菱形的定义、性质及判定.1.定义:有一组邻边相等的平行四边形叫做菱形.(1)菱形的四条边都相等;。(2)菱形的对角线互相垂直,并且每一条对角线平分一组对角(3)菱形被两条对角线分成四个全等的直角三角形.(4)菱形的面积等于两条对角线长的积的一半:2.菱形的面积。3.判定:(1)有一组邻边相等的平行四边形叫做菱形(2)四条边都相等的四边形是菱形;(3)对角线互相垂直的平行四边形是菱形.4.对称性:菱形是轴对称图形也是中心对称图形.考点4正方形定义、性质及判定.'1.定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.2.性质:(1)正方形四个角都是直角,四条边都相等;(2)正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;(3)正方形的一条对角线把正方形分成两个全等的等腰直角三角形;(4)正方形的对角线与边的夹角是45度;(5)正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.3.判定:(1)先判定一个四边形是矩形,再判定出有一组邻边相等;(2)先判定一个四边形是菱形,再判定出有一个角是直角.4.对称性:正方形是轴对称图形也是中心对称图形.考点5三角形的中位线平行于三角形的第三边并等于第三边的一半;梯形的中位线平行于梯形的两底并等于两底和的一半.线段的重心是线段的中点;平行四边形的重心是两对角线的交点;三角形的重心是三条中线的交点.依次连接任意一个四边形各边中点所得的四边形叫中点四边形.三、例题精析【例题1】【题干】正十边形的每个外角等于()A.18B.36C.45D.60【答案】B。-可编辑修改-【例题2】【题干】如果用4个相同的长为3宽为1的长方形,拼成一个大的长方形,那么这个大的长方形的周长可以是_____________.【答案】14或16或26【解析】根据外角和等于3600的性质,得正十边形的每个外角等于3600÷10=360。故选B。【例题3】【题干】如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为()A.31B.35C.5+1D.51【答案】D【解析】利用勾股定理求出CM的长,即ME的长,有DM=DE,所以可以求出DE,从而得到DG的长: 四边形ABCD是正方形,M为边AD的中点,∴DM=12DC=1。∴2222CMDCDM2+1=5。∴ME=MC=5。∴ED=EM-DM=51。 四边形EDGF是正方形,∴DG=DE=51。故选D。【例题4】【题干】如图,在平行四边形ABCD中,∠A=70°,将平行四边形折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于()A.70°B.40°C.30°D.20°【答案】B【解析】 四边形ABCD是平行四边形,∴AB∥CD。。-可编辑修改- 根据折叠的性质可得:MN∥AE,∠FMN=∠DMN,∴AB∥CD∥MN。 ∠A=70°,∴∠FMN=∠DMN=∠A=70°。∴∠AMF=180°-∠DMN-∠FMN=180°-70°-70°=40°。故选B。【例题5】【题干】如图,过口ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的口AEMG的面积S1与口HCFG的面积S2的大小关系是()A.S1>S2B.S1