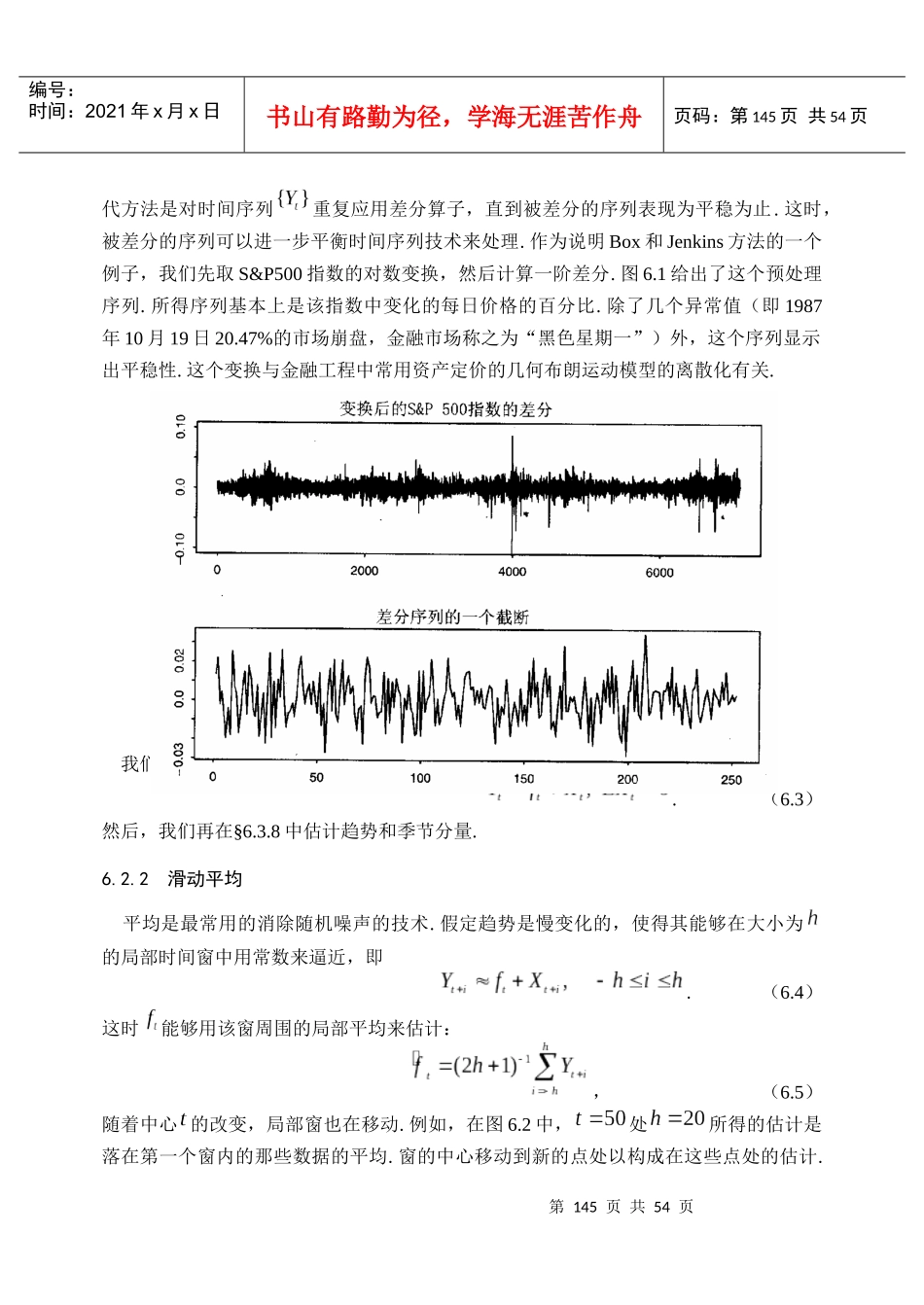
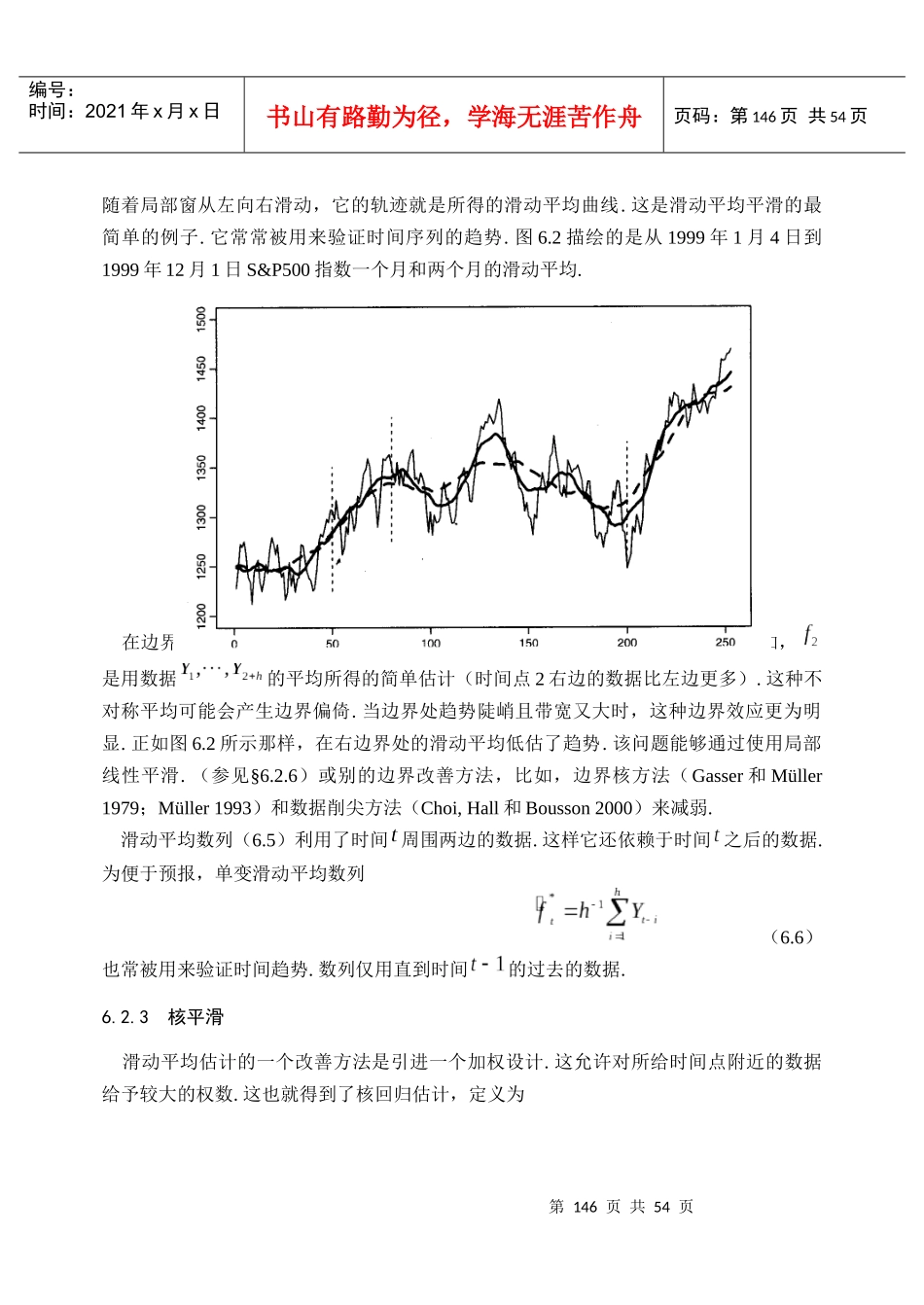
第144页共54页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第144页共54页第六章时间序列的平滑6.1引论上一章我们引进非参数函数估计的基本概念,现在将它应用到时间序列别的重要平滑问题上.对估计慢变化时间趋势,平滑技术是有用的图示工具,它产生了时域平滑(§6.2).对将来事件和与之相联系的现在与过去变量之间的关系的非参数统计推断导致了§6.3的状态域平滑.§6.4引入的样条方法是对§6.3引入的局部多项式方法的有用替代.这此方法能够容易地推广到时间序列的条件方差(波动性)的估计,甚至整个条件分布的估计,参阅§6.5.6.2时域平滑6.2.1趋势和季节分量分析时间序列的第一步是画数据图.这种方法使得人们可以从视觉上检查一个时间序列是否像一个平稳随机过程.如果观察到趋势或季节分量,在分析时间序列之前通常要将它们分离开来.假定时间序列能够分解成,(6.1)其中表示慢变函数,称为“趋势分量”,是周期函数,称为“季节分量”,是随机分量,它被假定是零均值的平稳序列.在使用这种分解之前,可以先用方差稳定变换或Box-Cox变换.这类幂变换有如下以参数为指标的形式(6.2)或具有在点处连续的变换形式.这类变换由Box和Cox(1964)给出.注意,由在幂变换中数据必须是非负的,因此,在使用幂变换之前,可能必须先实施平移变换.我们的目的是估计和提取确定性分量和.我们希望残差分量是平稳的,且能够用线性和非线性技术做进一步的分析.通过推广Box和Jenkins(1970)而发展的一个替第145页共54页第144页共54页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第145页共54页代方法是对时间序列重复应用差分算子,直到被差分的序列表现为平稳为止.这时,被差分的序列可以进一步平衡时间序列技术来处理.作为说明Box和Jenkins方法的一个例子,我们先取S&P500指数的对数变换,然后计算一阶差分.图6.1给出了这个预处理序列.所得序列基本上是该指数中变化的每日价格的百分比.除了几个异常值(即1987年10月19日20.47%的市场崩盘,金融市场称之为“黑色星期一”)外,这个序列显示出平稳性.这个变换与金融工程中常用资产定价的几何布朗运动模型的离散化有关.图6.11972年1月3日至1999年12月31日(上图)和1999年1月4日至1999年12月31日(下图)S&P500指数对数变换的差分我们首先把注意力集中在没有季节分量的情形,即.(6.3)然后,我们再在§6.3.8中估计趋势和季节分量.6.2.2滑动平均平均是最常用的消除随机噪声的技术.假定趋势是慢变化的,使得其能够在大小为的局部时间窗中用常数来逼近,即.(6.4)这时能够用该窗周围的局部平均来估计:,(6.5)随着中心的改变,局部窗也在移动.例如,在图6.2中,处所得的估计是落在第一个窗内的那些数据的平均.窗的中心移动到新的点处以构成在这些点处的估计.第146页共54页第145页共54页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第146页共54页随着局部窗从左向右滑动,它的轨迹就是所得的滑动平均曲线.这是滑动平均平滑的最简单的例子.它常常被用来验证时间序列的趋势.图6.2描绘的是从1999年1月4日到1999年12月1日S&P500指数一个月和两个月的滑动平均.图6.21999年1月4日至12月31日S&P500指数和它的21个交易日(粗线)和41个交易日(虚线)的滑动平均在边界处,滑动平均估计的习惯做法是忽略超出观察时间范围的那些数据.例如,是用数据的平均所得的简单估计(时间点2右边的数据比左边更多).这种不对称平均可能会产生边界偏倚.当边界处趋势陡峭且带宽又大时,这种边界效应更为明显.正如图6.2所示那样,在右边界处的滑动平均低估了趋势.该问题能够通过使用局部线性平滑.(参见§6.2.6)或别的边界改善方法,比如,边界核方法(Gasser和Müller1979;Müller1993)和数据削尖方法(Choi,Hall和Bousson2000)来减弱.滑动平均数列(6.5)利用了时间周围两边的数据.这样它还依赖于时间之后的数据.为便于预报,单变滑动平均数列(6.6)也常被用来验证时间趋势.数列仅用直到时间的过去的数据.6.2.3核平滑滑动平均估计的一个改善方法是引进一个加权设计.这允许对所给时间点附近的数据给予较大的权...