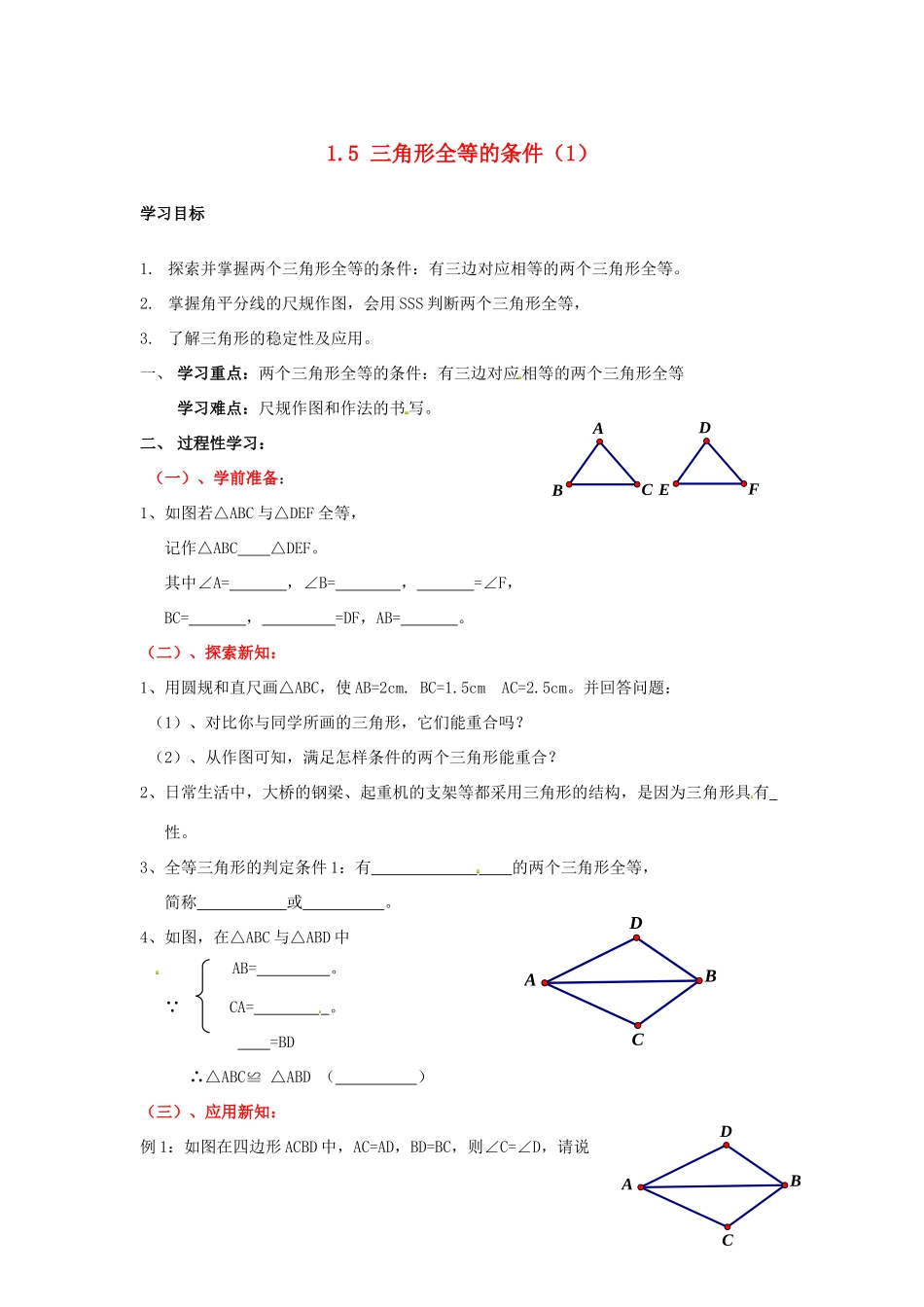
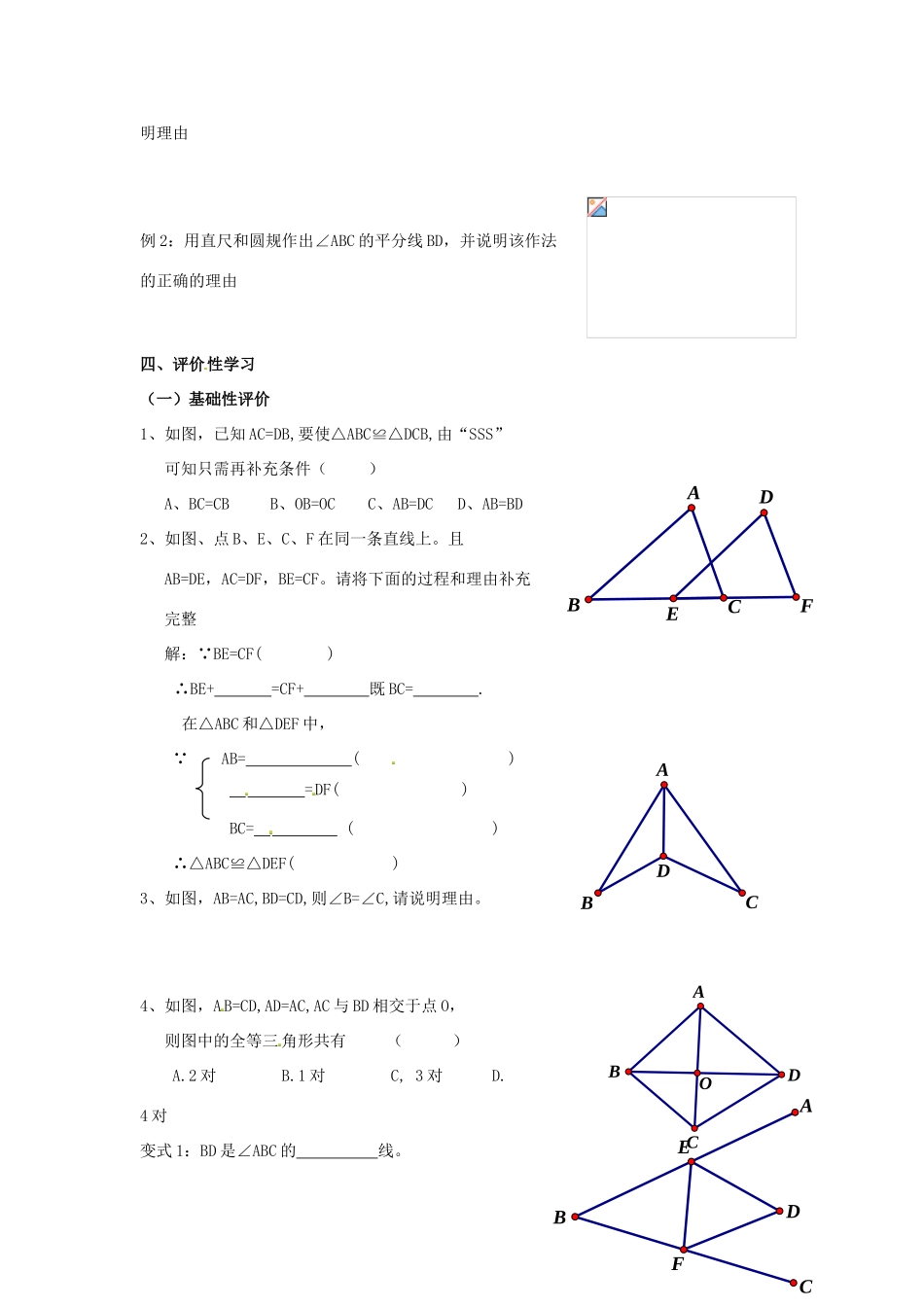
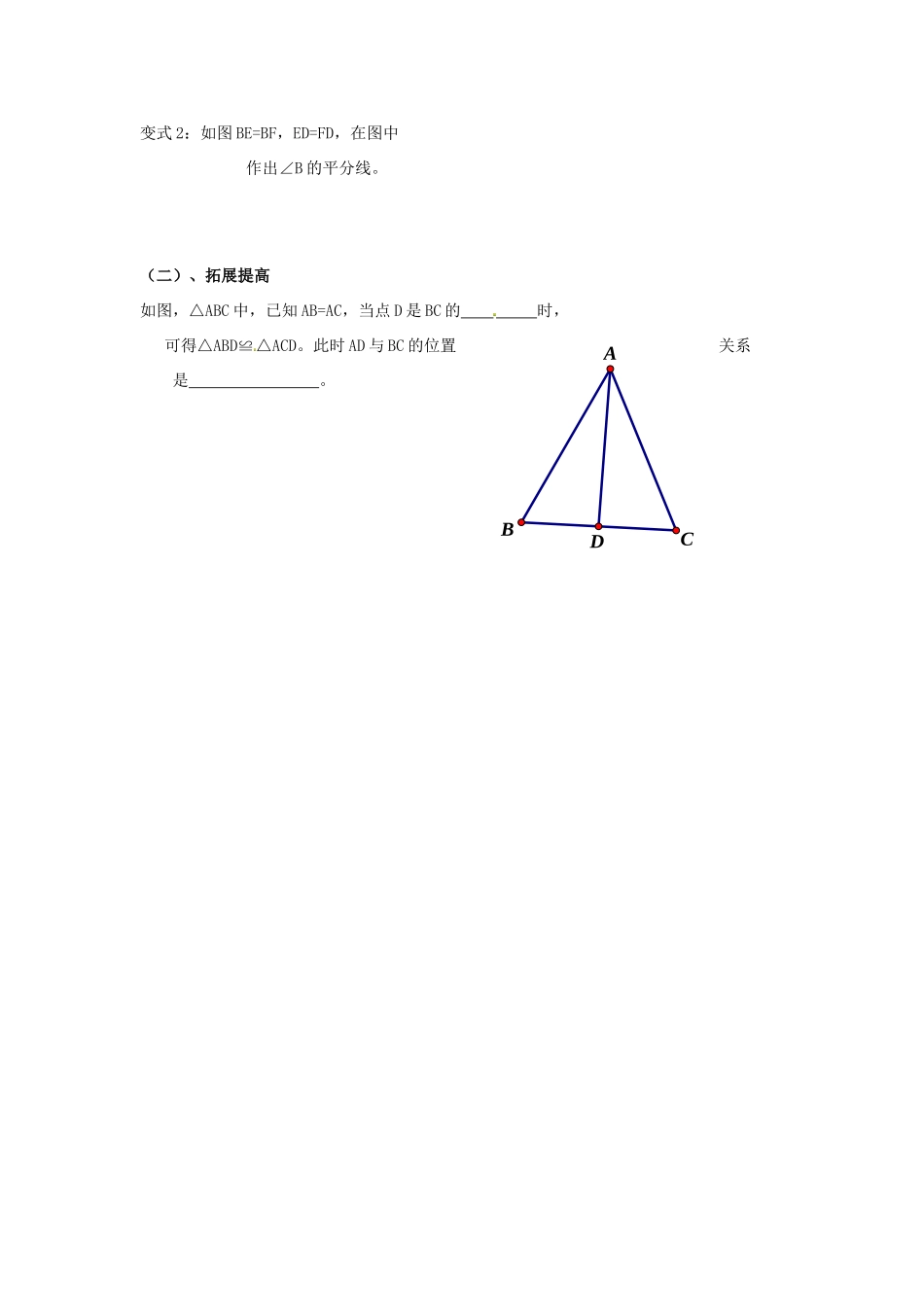
1.5三角形全等的条件(1)学习目标1.探索并掌握两个三角形全等的条件:有三边对应相等的两个三角形全等。2.掌握角平分线的尺规作图,会用SSS判断两个三角形全等,3.了解三角形的稳定性及应用。一、学习重点:两个三角形全等的条件:有三边对应相等的两个三角形全等学习难点:尺规作图和作法的书写。二、过程性学习:(一)、学前准备:1、如图若△ABC与△DEF全等,记作△ABC△DEF。其中∠A=,∠B=,=∠F,BC=,=DF,AB=。(二)、探索新知:1、用圆规和直尺画△ABC,使AB=2cm.BC=1.5cmAC=2.5cm。并回答问题:(1)、对比你与同学所画的三角形,它们能重合吗?(2)、从作图可知,满足怎样条件的两个三角形能重合?2、日常生活中,大桥的钢梁、起重机的支架等都采用三角形的结构,是因为三角形具有性。3、全等三角形的判定条件1:有的两个三角形全等,简称或。4、如图,在△ABC与△ABD中AB=。∵CA=。=BD∴△ABC≌△ABD()(三)、应用新知:例1:如图在四边形ACBD中,AC=AD,BD=BC,则∠C=∠D,请说BCADFEDABCDABC明理由例2:用直尺和圆规作出∠ABC的平分线BD,并说明该作法的正确的理由四、评价性学习(一)基础性评价1、如图,已知AC=DB,要使△ABC≌△DCB,由“SSS”可知只需再补充条件()A、BC=CBB、OB=OCC、AB=DCD、AB=BD2、如图、点B、E、C、F在同一条直线上。且AB=DE,AC=DF,BE=CF。请将下面的过程和理由补充完整解:∵BE=CF()∴BE+=CF+既BC=.在△ABC和△DEF中,∵AB=()=DF()BC=()∴△ABC≌△DEF()3、如图,AB=AC,BD=CD,则∠B=∠C,请说明理由。4、如图,AB=CD,AD=AC,AC与BD相交于点O,则图中的全等三角形共有()A.2对B.1对C,3对D.4对变式1:BD是∠ABC的线。BCADFEABCDOBDACABCDEF变式2:如图BE=BF,ED=FD,在图中作出∠B的平分线。(二)、拓展提高如图,△ABC中,已知AB=AC,当点D是BC的时,可得△ABD≌△ACD。此时AD与BC的位置关系是。ABCD