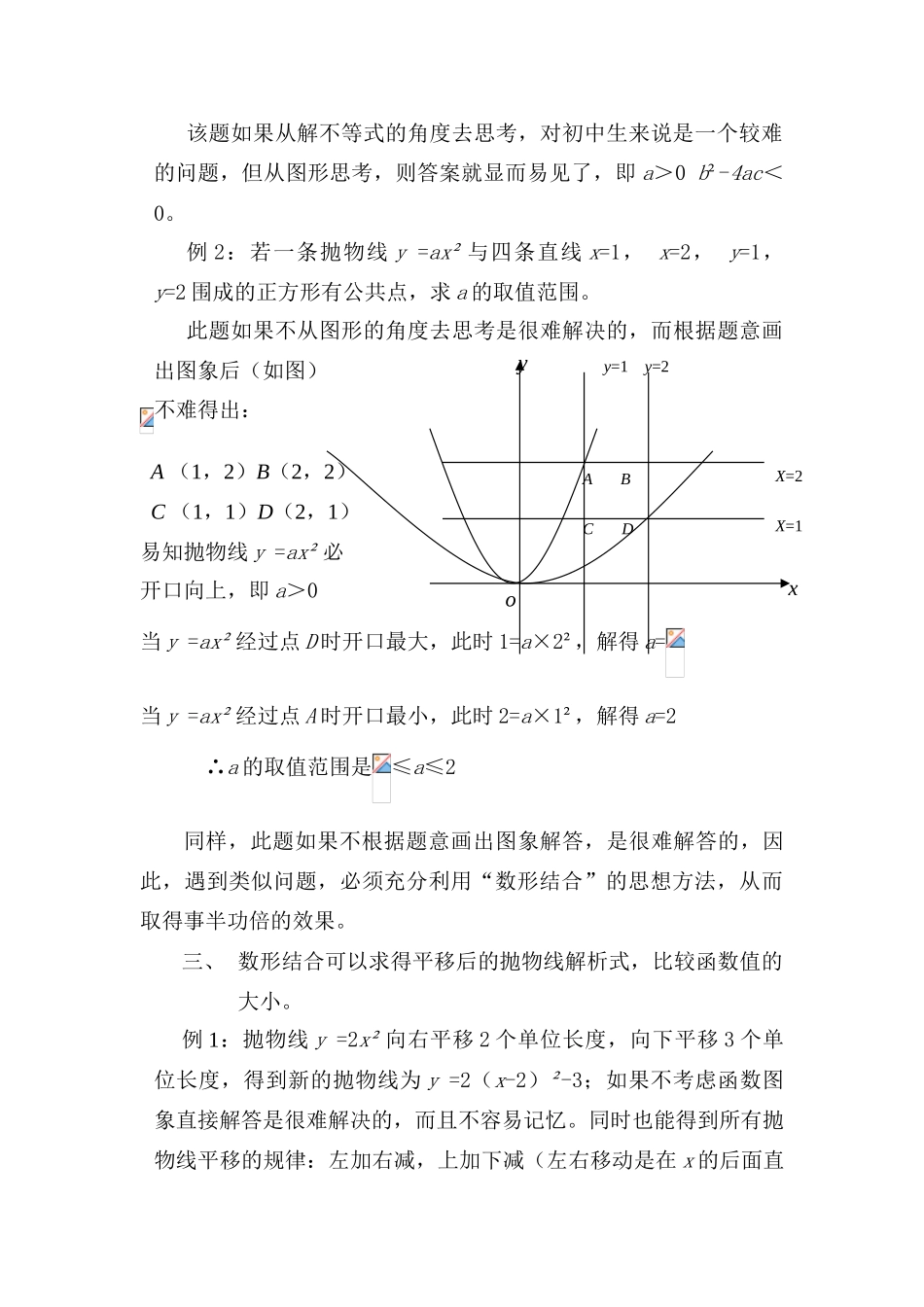
数形结合思想在二次函数中的应用著名的数学家华罗庚说过:“数缺形时少直觉,形缺数时难入微。数形结合百般好,隔离分家万事非。”寥寥数语把数形结合说得淋漓尽致。数形结合是数学解题中常用一种数学思想方法,可以使抽象的数学问题直观化,生动化,能够变抽象思维为形象思维,有助于把握数学问题中的本质。数学教学不仅是数学知识的教学,更重要的是数学思想方法的教学,教学中教师应注重对学生的观察、操作、分析思维能力的培养,更应不断地渗透数学思想方法,将此作为教学的核心,为学生的后继学习打下坚实的基础,使学生终身受益。二次函数是初中数学的重要内容之一,也是学习的一个难点,同时又是“数形结合”思想方法体现的很充分的一个章节。在此特对数形结合解决二次函数的问题进行简单的归纳分析。一、由函数图象可得函数中的a、b、c及有关代数式的值。例:(如图)由函数图象可以直接得二次函数的基本性质(如:函数的变化趋势……),此外,在y=ax²+bx+c(a≠0)中还能得以下结论:(1) 抛物线开口向上∴a>0(2) 抛物线顶点在第四象限∴->0即<0∴b<0(3) 抛物线与y交于y轴的负半轴∴c<0(4) 当x=1时,y<0∴a+b+c<0 当x=-1时,y>0∴a-b+c>0 当x=2时,y>0∴4a+2b+c>0 当x=-2时,y<0∴4a-2b+c<0…………(5) 抛物线与x轴有两个交点∴b²-4ac>0-1Oxy-11(6) 抛物线的对称轴在直线x=1的左边∴-<1∴2a+b>0 抛物线的顶点在直线y=-1的下方∴<-1∴4ac-b²<-4a…………二、由函数图象可以得出方程的解,不等式的解。例:(如图)由函数图象可得:(抛物线的对称轴……)基本性质外,在=ax²+bx+c(a≠0)还可得到以下两点:(1) 抛物线与x轴交于(-1,0),(3,0)∴方程ax²+bx+c=0解为:=-1=3(2) 当-1<x<3时,y<0;当x<-1或x>3时,y>0∴ax²+bx+c>0的解集是-1<x<3ax²+bx+c<0的解集是x<-1或x>3当然,由函数图象也可以得到这个二次函数的解析式。如果在图象中再出现直线=2x+1,则根据图象也能得到什么情况下>;什么情况下<;什么情况下=。三、利用函数图象可以使一些问题简单化。例1:(如图)无论x为何值,y=ax²+bx+c恒为正的条件是:()Aa>0b²-4ac>0Ba<0b²-4ac>0Ca>0b²-4ac<0Da<0b²-4ac<0-131O-3ByxACoyx该题如果从解不等式的角度去思考,对初中生来说是一个较难的问题,但从图形思考,则答案就显而易见了,即a>0b²-4ac<0。例2:若一条抛物线y=ax²与四条直线x=1,x=2,y=1,y=2围成的正方形有公共点,求a的取值范围。此题如果不从图形的角度去思考是很难解决的,而根据题意画出图象后(如图)不难得出:A(1,2)B(2,2)C(1,1)D(2,1)易知抛物线y=ax²必开口向上,即a>0当y=ax²经过点D时开口最大,此时1=a×2²,解得a=当y=ax²经过点A时开口最小,此时2=a×1²,解得a=2∴a的取值范围是≤a≤2同样,此题如果不根据题意画出图象解答,是很难解答的,因此,遇到类似问题,必须充分利用“数形结合”的思想方法,从而取得事半功倍的效果。三、数形结合可以求得平移后的抛物线解析式,比较函数值的大小。例1:抛物线y=2x²向右平移2个单位长度,向下平移3个单位长度,得到新的抛物线为y=2(x-2)²-3;如果不考虑函数图象直接解答是很难解决的,而且不容易记忆。同时也能得到所有抛物线平移的规律:左加右减,上加下减(左右移动是在x的后面直y=1y=2xyoX=2X=1ABCD接加减,上下移动是在整个式子的后面加减)。例2:已知二次函数在y=ax²+bx+c(a≠0)的图象过点A(1,2),B(3,2),C(5,7)。若点M(-2,),N(-1,),K(8,)也在二次函数的图象上,则、、的大小关系?分析:此题可以根据已知条件A、B、C三点的坐标求得函数解析式,然后再把M、N、K三点中的横坐标代入求得纵坐标的值,既而得到、、的大小关系;当然如果此题联系函数图象解答会更简单一些,由A、B、C三点的坐标可以得到抛物线的对称轴为直线x=2,且开口向上,因此在对称轴的左边也就是x<2时,y随x的增大而减小,在对称轴的右边也就是x>2时,y随x的增大而增大,故>,又因为点K(8,)距对称轴的距离大于点M(-2,)距对称轴的距离,...