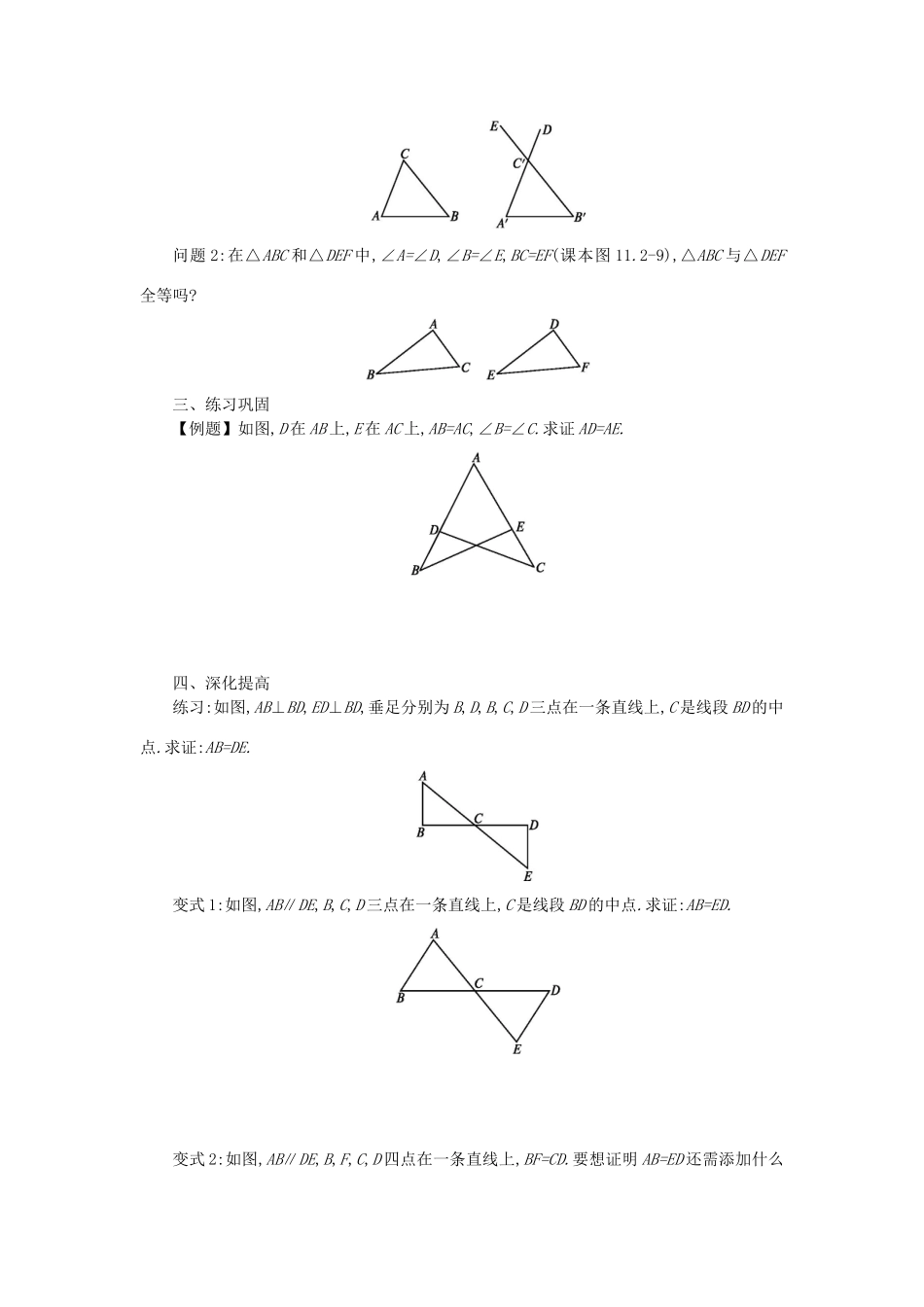
第十二章全等三角形12.2三角形全等的判定12.2三角形全等的判定(第3课时)学习目标1.熟记角边角公理、角角边推论的内容.2.能应用角边角公理及其推论证明两个三角形全等.学习过程一、自主学习师:观察下列一组图片,同学们,今天先请大家帮个忙,小明踢球时不慎把一块三角形的玻璃打碎为两块,他要去玻璃店买一块大小相同的玻璃,那么:问题:(1)要不要两块都带去?(2)带哪块去呢?(3)带第②块,带去了三角形的几个元素?带第①块呢?问:恢复后的三角形和原三角形全等,那全等的条件是不是由带去的元素决定的呢?二、深化探究先任意画一个△ABC,再画出一个△A'B'C',使A'B'=AB,∠A'=∠A,∠B'=∠B,把画出的△A'B'C'剪下,放到△ABC上,它们全等吗?学生动手操作,感知问题的规律,画图步骤如下:(1)画A'B'=AB;(2)在A'B'的同旁画∠DA'B'=∠A,∠EB'A'=∠B,A'D,B'E交于点C'.归纳:两角与它们的夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).问题1:课本图11.2-8中,∠A'=∠A,∠B'=∠B,那么∠C=∠A'C'B'吗?为什么?问题2:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF(课本图11.2-9),△ABC与△DEF全等吗?三、练习巩固【例题】如图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证AD=AE.四、深化提高练习:如图,AB⊥BD,ED⊥BD,垂足分别为B,D,B,C,D三点在一条直线上,C是线段BD的中点.求证:AB=DE.变式1:如图,AB∥DE,B,C,D三点在一条直线上,C是线段BD的中点.求证:AB=ED.变式2:如图,AB∥DE,B,F,C,D四点在一条直线上,BF=CD.要想证明AB=ED还需添加什么条件?说说你的理由.五、反思小结1.知识技能:对应相等元素三边三角两边一角两角一边两边及其夹角两边及其中一边的对角两角及其夹边两角及其中一角的对边三角形是否全等2.数学思想:3.证题技巧:六、课堂检测1.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得ED的长度就是AB的长度,为什么?2.如图,AB⊥BC,AD⊥DC,∠BAC=∠DAC,求证:AB=AD.参考答案一、自主学习图中的第①块玻璃只能确定三角形的一个角,是无法确定整块玻璃的大小和形状的;图中的第②块玻璃能确定三角形的两个角和它们的夹边(ASA),能够确定整块玻璃的大小和形状.二、深化探究问题1:根据三角形内角和定理,∠C'=180°-∠A'-∠B',∠C=180°-∠A-∠B,由于∠A=∠A',∠B=∠B',∴∠C=∠C'.问题2:运用三角形内角和定理,以及“ASA”可很快证出△ABC≌△DEF.三、练习巩固证明:在△ACD和△ABE中,{∠A=∠A(),公共角AC=AB,∠C=∠B,∴△ACD≌△ABE(ASA).∴AD=AE.四、深化提高练习答案:证明:∵∠B=∠D,BC=DC,∠ACB=∠ECD,∴△ABC≌△EDC.∴AB=DE.变式1:证明:∵AB∥DE,∴∠B=∠D.∵∠B=∠D,BC=DC,∠ACB=∠ECD,∴△ABC≌△EDC.∴AB=DE.变式2:可以添加条件(1)∠A=∠E.(AAS)(2)AC∥FE或∠ACB=∠EFD.(ASA)五、反思小结略六、课堂检测1.证明:∵∠B=∠CDE,BC=DC,∠ACB=∠ECD,∴△ABC≌△EDC.∴AB=ED.2.证明:∵∠B=∠D,∠BAC=∠DAC,AC=AC,∴△ABC≌△ADC.∴AB=AD.