辽宁省灯塔市八年级数学下册 3.2 图形的旋转（第1课时）导学案 （新版）北师大版-（新版）北师大版初中八年级下册数学学案VIP免费

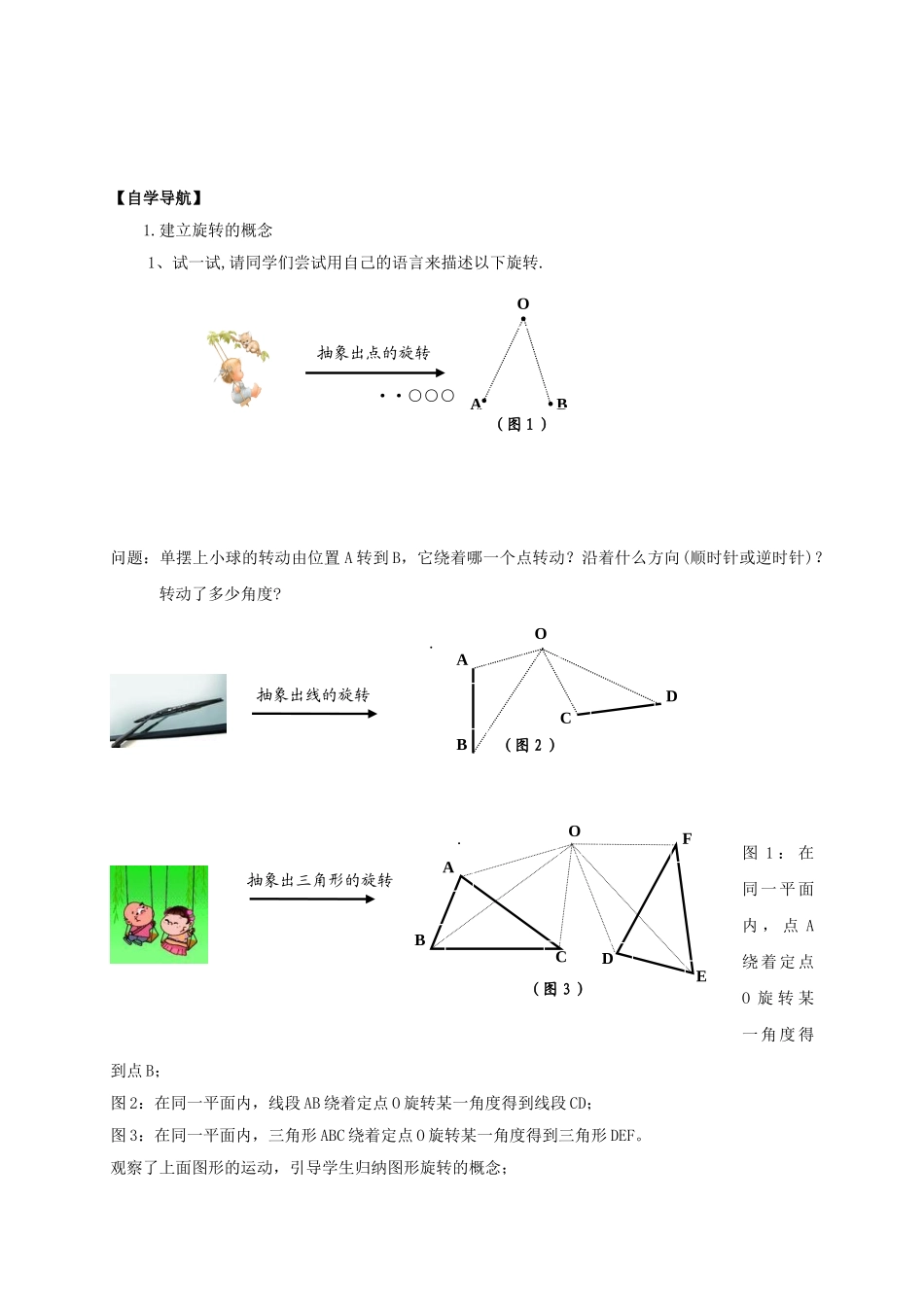
3.2图形的旋转【学习目标】课标要求：1、通过具体事例认识旋转2、理解旋转前后两个图形对应点到旋转中心的距离相等3、对应点与旋转中心的连线所成的角彼此相等的性质目标达成：1、类比平移与旋转的异同，掌握旋转的定义和基本性质，并利用数学知识解释生活中的旋转现象2、探索旋转的性质，特别是，对应点到旋转中心的距离相等学习流程：【课前展示】小题分组回答【创境激趣】演示俄罗斯方块游戏，构成游戏的模块均是由一个小正方形平移变换而来，通过学生玩游戏，发现除了平移运动之外还有旋转运动.引导学生列举出一些具有旋转现象的生活实例，引出课题：“生活中的旋转”。向学生展示有关的图片：(1)时钟上的秒针在不停的转动；（并介绍顺时针方向和逆时针方向）(2)大风车的转动；(3)飞速转动的电风扇叶片；（4）汽车上的括水器；（5)由平面图形转动而产生的奇妙图案。【自学导航】1.建立旋转的概念1、试一试,请同学们尝试用自己的语言来描述以下旋转.··○○○问题：单摆上小球的转动由位置A转到B，它绕着哪一个点转动？沿着什么方向(顺时针或逆时针)？转动了多少角度?图1：在同一平面内，点A绕着定点O旋转某一角度得到点B；图2：在同一平面内，线段AB绕着定点O旋转某一角度得到线段CD；图3：在同一平面内，三角形ABC绕着定点O旋转某一角度得到三角形DEF。观察了上面图形的运动，引导学生归纳图形旋转的概念；抽象出点的旋转AB（图1）O抽象出三角形的旋转·OABCFDE（图3）抽象出线的旋转·OABCD（图2）像这样，把一个图形绕着某一点O转动一个角度的图形变换叫做旋转（rotation）.点O叫做旋转中心，转动的角叫做旋转角。重点突出旋转的三个要素：旋转中心、旋转方向和旋转角度。（2）情景问题：①请同学们观察图3，点A，线段AB，∠ABC分别转到了什么位置？②请找出图3中其他的对应点、对应线段、对应角，并指出旋转中心和旋转角度。设计意图：点明图形旋转中对应点、对应线段及对应角的概念；让学生及时巩固并理解旋转及其相关概念，并为下面探究旋转的性质作好物质与精神上的准备。【合作探究】2．应用旋转的概念解决问题这一环节让学生进行问题的研究与解答，培养应用数学知识的意识及解决数学问题的能力。（1）如图，△ABO绕点O旋转得到△CDO，则：点B的对应点是点_____；线段OB的对应线段是线段______；线段AB的对应线段是线段______；∠A的对应角是______；∠B的对应角是______；旋转中心是点______；旋转的角是______。设计意图：①及时巩固新知，使每个学生都有收获；②感受成功的喜悦，肯定探索活动的意义。（2）如图，如果正方形CDEF与正方形ABCD是一边重合的两个正方形，那么正方形CDEF能否看成是正方形ABCD旋转得到？如果能，请指出旋转中心、旋转方向、旋转角度及对应点。CABODDCABEF·OABCFDE（3）如图，香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中的一瓣经过几次旋转得到的?旋转角∠AOB多少度？你知道∠COD等于多少度吗？设计意图：加深对旋转概念的理解，及时巩固新知识，对于第2题要注重引导学生多角度分析解决，第3题求∠AOB的度数学生可以根据五分周角容易得到，而学生在求∠COD的度数时，更多的是凭数学直觉或猜测。由此，可以比较自然地引导学生通过实验操作，利用度量等方法去探究旋转的有关性质。【展示提升】典例分析知识迁移做一做：如图，在硬纸板上，挖出一个三角形ABC，再挖一个小洞O作为旋转中心，硬纸板下面放一张白纸。先在纸上描出这个挖掉的三角形图案（△ABC），然后围绕旋转中心转动硬纸板再描出这个挖掉的三角形（△DEF），移开硬纸板。问题：请指出旋转中心和各对应点，哪一个角是旋转角？1．从我们看到的旋转现象以及你所完成的实验中，你认为旋转主要因素是什么？2．在图形的旋转过程中，哪些发生了改变？哪些没有发生改变？量一量线段OA与线段OD的关系怎样（这里包括数量关系和位置关系），线段OB和OE，OC和OF呢？AB与DE呢？··ABODC3．你能通过度量角的方法得出旋转角度吗？你准备度量哪个角？探索得出下列性质：1、旋转前后的图形全等；2、对应点到旋转中心的距离相等；3、对应点与旋转中心连线段的夹角等于旋...