九年级数学下册：3.3圆周角和圆心角的关系（第1课时）导学案（北师大版）VIP免费

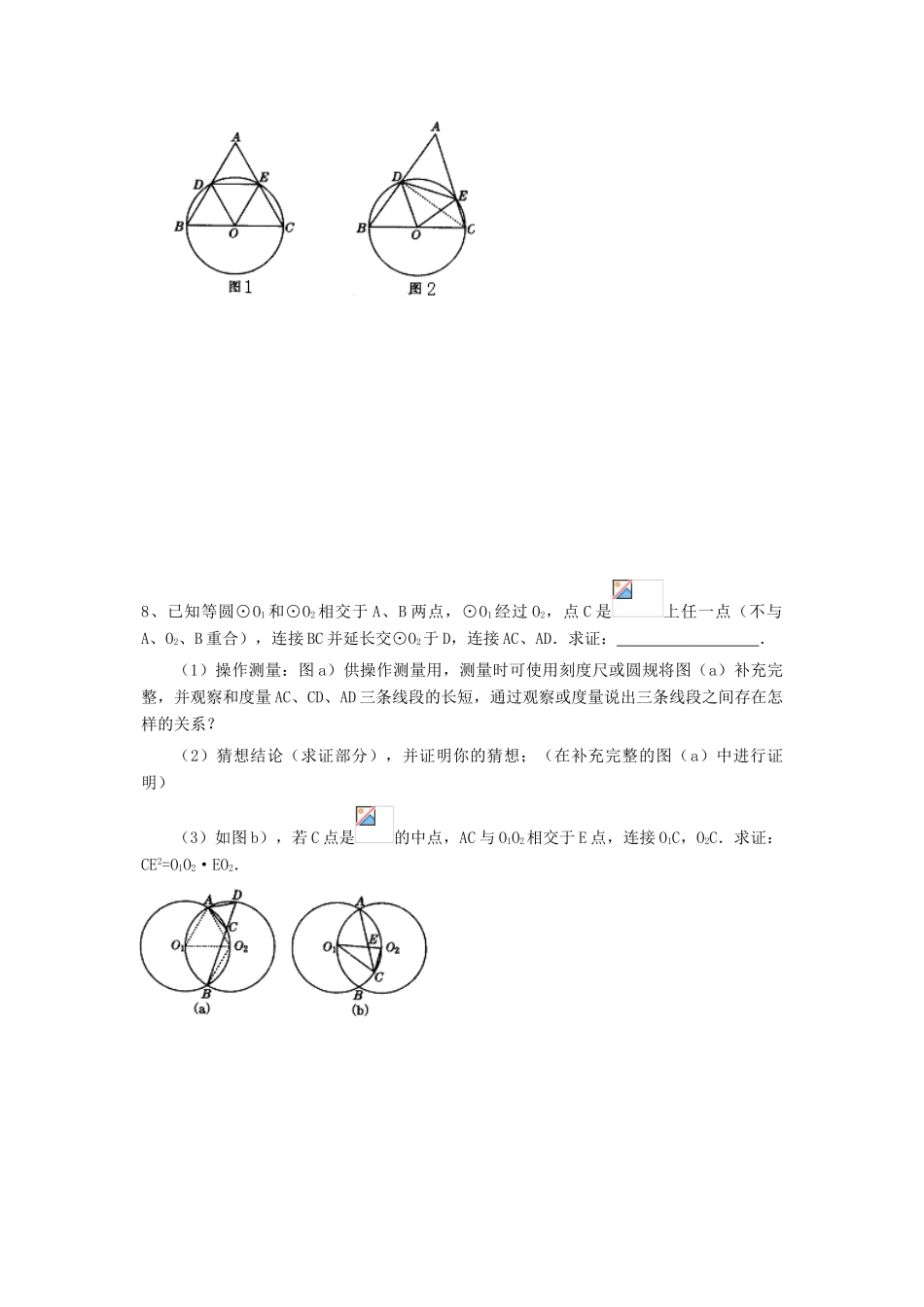
3.3圆周角和圆心角的关系（第一课时）学习目标:（1）理解圆周角的概念,掌握圆周角的两个特征、定理的内容及简单应用；（2）继续培养学生观察、分析、想象、归纳和逻辑推理的能力；（3）渗透由“特殊到一般”，由“一般到特殊”的数学思想方法．学习重点:圆周角的概念和圆周角定理学习难点:圆周角定理的证明中由“一般到特殊”的数学思想方法和完全归纳法的数学思想．学习方法:指导探索法.学习过程:一、举例：1、已知⊙O中的弦AB长等于半径，求弦AB所对的圆周角和圆心角的度数．2、如图，OA、OB、OC都是圆O的半径，∠AOB=2∠BOC．求证：∠ACB=2∠BAC3、如图，已知圆心角∠AOB=100°，求圆周角∠ACB、∠ADB的度数？4、一条弦分圆为1：4两部分，求这弦所对的圆周角的度数？5、已知AB为⊙O的直径，AC和AD为弦，AB=2，AC=，AD=1，求∠CAD的度数．6、如图，A、B、C、D、E是⊙O上的五个点，则图中共有个圆周角，分别是．7、如图，已知△ABC是等边三角形，以BC为直径的⊙O交AB、AC于D、E．（1）求证：△DOE是等边三角形；（2）如图3-3-14，若∠A=60°，AB≠AC，则①中结论是否成立？如果成立，请给出证明；如果不成立，请说明理由？8、已知等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过O2，点C是上任一点（不与A、O2、B重合），连接BC并延长交⊙O2于D，连接AC、AD．求证：．（1）操作测量：图a）供操作测量用，测量时可使用刻度尺或圆规将图（a）补充完整，并观察和度量AC、CD、AD三条线段的长短，通过观察或度量说出三条线段之间存在怎样的关系？（2）猜想结论（求证部分），并证明你的猜想；（在补充完整的图（a）中进行证明）（3）如图b），若C点是的中点，AC与O1O2相交于E点，连接O1C，O2C．求证：CE2=O1O2·EO2．二、课外练习：1、⊙O的弦AB等于半径，那么弦AB所对的圆周角一定是（）．（A）30°（B）150°（C）30°或150°（D）)60°2、△ABC中，∠B＝90°，以BC为直径作圆交AC于E，若BC=12，AB=12，则的度数为（）．（A）60°（B）80°（C）100°（D）)120°3、如图，△ABC是⊙O的内接等边三角形，D是AB上一点，AB与CD交于E点，则图中60°的角共有()个．（A）3（B）4（C）5（D）64、如图，△ABC内接于⊙O，∠OBC=25°，则∠A的度数为（）（A）70°（B）65°（C）60°（D）)50°5、圆内接三角形三个内角所对的弧长为3:4:5，那么这个三角形内角的度数分别为__________．6、如图，AB是⊙O的直径，CD⊥AB于D，AD=9cm，DB=4cm，求CD和AC的长．7、已知：如图，△ABC是⊙O的内接三角形，⊙O的直径BD交AC于E，AF⊥BD于F，延长AF交BC于G．求证：