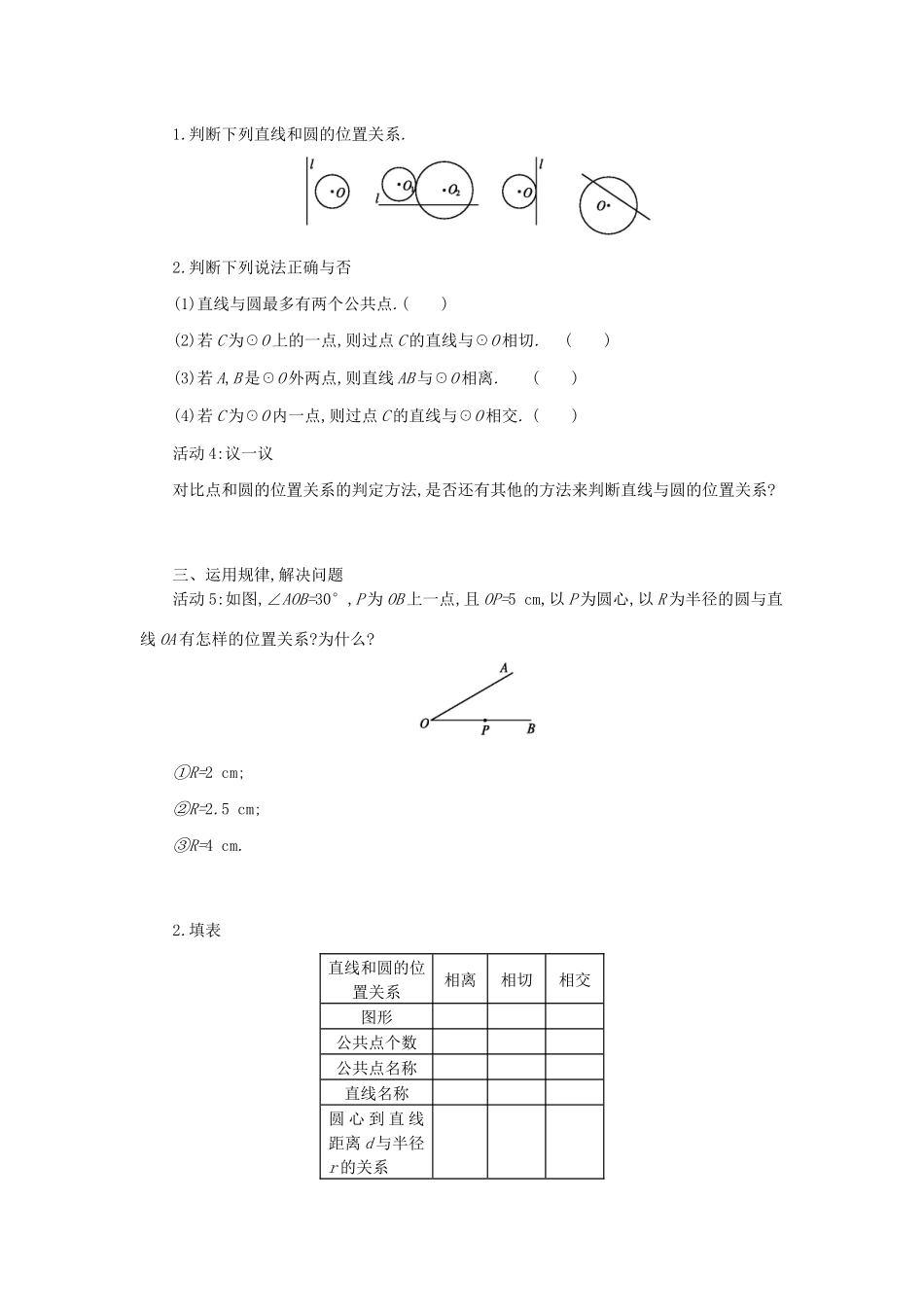
第二十四章圆24.2点和圆、直线和圆的位置关系24.2.2直线和圆的位置关系(第1课时)学习目标1.理解直线与圆的相交、相切、相离三种位置关系.2.掌握它们的判定方法.学习过程设计一、设计问题,创设情境活动1:1.点与圆有几种位置关系?2.怎样判定点和圆的位置关系?活动2:你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?二、信息交流,揭示规律活动3:(1)直线和圆的公共点个数的变化情况如何?公共点个数最少时有几个?最多时有几个?(2)通过刚才的研究,你认为直线和圆的位置关系可分为几种类型?1.判断下列直线和圆的位置关系.2.判断下列说法正确与否(1)直线与圆最多有两个公共点.()(2)若C为☉O上的一点,则过点C的直线与☉O相切.()(3)若A,B是☉O外两点,则直线AB与☉O相离.()(4)若C为☉O内一点,则过点C的直线与☉O相交.()活动4:议一议对比点和圆的位置关系的判定方法,是否还有其他的方法来判断直线与圆的位置关系?三、运用规律,解决问题活动5:如图,∠AOB=30°,P为OB上一点,且OP=5cm,以P为圆心,以R为半径的圆与直线OA有怎样的位置关系?为什么?①R=2cm;②R=2.5cm;③R=4cm.2.填表直线和圆的位置关系相离相切相交图形公共点个数公共点名称直线名称圆心到直线距离d与半径r的关系四、变式训练,深化提高1.在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以点C为圆心,r为半径作圆.(1)当r满足时,直线AB与☉C相离;(2)②当r满足时,直线AB与☉C相切;(3)当r满足时,直线AB与☉C相交;(4)当r满足时,线段AB与☉C有且只有一个公共点.2.试着编一道直线与圆位置关系的题目,使得直线与圆满足相离、相切、相交三种位置关系.五、反思小结,观点提炼参考答案一、设计问题,创设情境活动1:1.3种2.(1)点到圆心的距离大于半径时,点在圆外.(2)点到圆心的距离等于半径时,点在圆上.(3)点到圆心的距离小于半径时,点在圆内.活动2:直线和圆有三种位置关系.二、信息交流,揭示规律活动3:(1)一开始没有公共点,到有一个公共点,然后有两个公共点;0;2(2)3种1.相离;与☉O1相离,与☉O2相交;相切;相交.2.(1)√(2)×(3)×(4)√活动4:利用圆心到直线的距离与半径的大小关系来判断直线与圆的位置关系.三、运用规律,解决问题1.解:过点P作PM⊥OA于点M.在Rt△OMP中,∠AOB=30°,OP=5cm∴PM=2.5cm.(1)R=2cm,∵2<2.5,∴☉P与OA相离.(2)R=2.5cm,∵2.5=2.5,∴☉P与OA相切.(3)R=4cm,∵4>2.5,∴☉P与OA相交.2.直线和圆的位置关系相离相切相交图形公共点个数012公共点名称切点割点直线名称切线割线圆心到直线距离d与半径r的关系d>rd=rd6013(4)r=6013或5