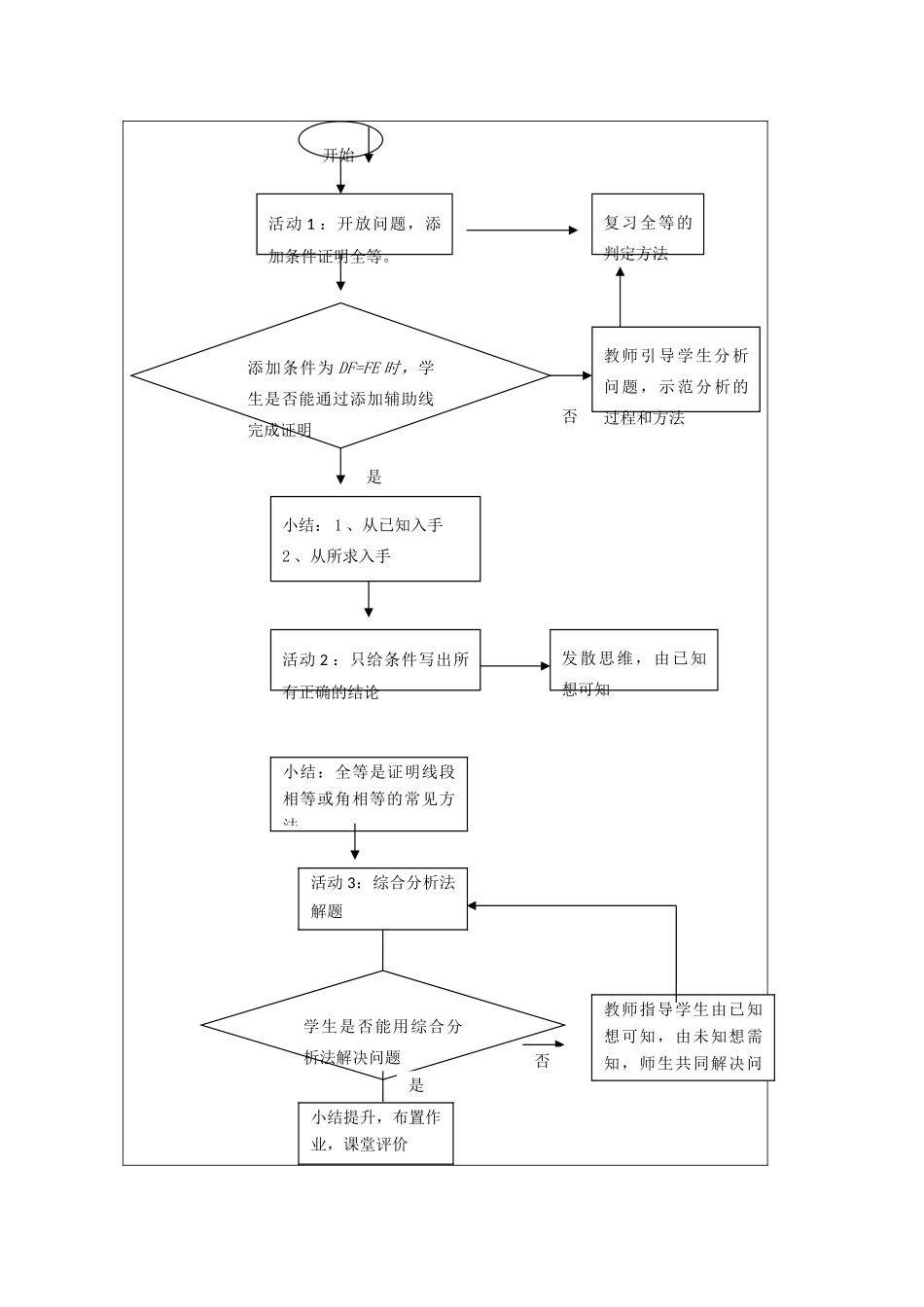
全等三角形的判定与性质指导思想与理论依据《数学课程标准》指出:“推理能力的发展应贯穿在整个数学学习过程中。推理是数学的基本思维方式,也是人们学习和生活中经常使用的思维方式。推理一般包括合情推理和演绎推理,在解决问题的过程中两种推理功能不同,相辅相成:合情推理用于探究思路,发现结论;演绎推理用于证明结论。”在学段目标中还提出:“体会通过合情推理探究数学结论,运用演绎推理加以证明的过程,在多种形式的数学活动中,发展合情推理与演绎推理的能力。”本节课设计了三个数学活动,将推理能力的培养有机的融合在这些活动中,让学生自己思考总结提炼解决问题的方法,给学生充分的交流空间,组织学生经历观察、猜想、证明等数学活动,在活动中提升逻辑推理的能力。教学背景分析教学内容:本节课选自北京课改版教材八年级上册第十三章《三角形》的第4-5节《全等三角形的性质与判定》的复习课,通过习题复习全等三角形判定常用的四种方法,综合运用全等三角形的判定和性质解题。全等是证明线段相等或角相等常用的方法,也是后续学习相似三角形性质和判定以及四边形的重要基础。全等三角形的判定和性质的综合运用也是发展学生推理能力重要的载体,为今后学习四边形这一章提供了宝贵的数学活动经验。本届课的教学重点是全等三角形判定和性质的综合运用,教学难点是用综合分析法解决全等三角形的有关问题。学生情况:学生在本节复习课之前已经学习了全等三角形的概念和性质,经历了探究全等三角形判定方法的过程,掌握了基本的四种判定方法,可以解决简单的三角形全等问题。初步具有一定的推理能力,能通过分析解决一些简单的一次全等的基本题目。本节课是对前几节课程所学内容的灵活应用和综合运用,指导学生用综合分析法分析问题解决问题,渗透图形变换的数学思想和转化的数学思想方法,进一步提升学生的逻辑推理能力。教学方式:以学生为主体的讲授式教学学生主讲教师主导教学手段:多媒体辅助教学技术准备:几何画板演示课件整合白板操作教学目标学生经历观察、探究、证明、总结等过程,对全等三角形的性质和判定进行系统复习。学生初步会运用运动的观点从整体观察图形之间的关系,发展空间观念,形成几何直观,在综合分析法的运用的实践中进一步发展逻辑推理能力。学生在分析习题、探究方法的实践中获取数学活动经验,学生敢于大胆猜想、乐于探究,体会数学活动中的乐趣。教学流程示意添加条件为DF=FE时,学生是否能通过添加辅助线完成证明活动1:开放问题,添加条件证明全等。开始复习全等的判定方法是否小结:1、从已知入手2、从所求入手教师引导学生分析问题,示范分析的过程和方法活动2:只给条件写出所有正确的结论发散思维,由已知想可知小结:全等是证明线段相等或角相等的常见方法活动3:综合分析法解题学生是否能用综合分析法解决问题否教师指导学生由已知想可知,由未知想需知,师生共同解决问题是小结提升,布置作业,课堂评价教学过程本节课设计了三个数学活动,通过活动1添加需要的条件证明全等的过程引导学生由未知想需知,添加不同的条件也复习了不同的判定全等的方法。其中一种添加条件的题目时一个综合题目需要用两次全等,由第一次全等为第二次全等提供条件也渗透了转化的数学思想,分析这个综合题时分别从已知和所求入手进行分析,发展了学生的两种推理能力。在活动2中设计开放性问题发散学生思维,主要发展学生演绎推理的能力。在活动3中运用综合分析法解题,学生从不同的角度分析已知和所求会有不同的解题方法,在一题多解的过程中继续体会应用合情推理探究结论和运用演绎推理进行证明的过程。教学过程教学阶段教师活动学生活动设置意图技术应用时间安排一、复习梳理活动1:开放问题,复习三角形全等的判定方法。如图:点D、E分别是AB、AC上的点,且AD=AE,请再添加一个条件(不再添加新的线段或字母)使得△ABE≌△ACD.师生共同审题后提出要求,学生添加条件并说明依据。教师关注学生是否能边审题边将已知标图,关注学生已有的水平能写出几种可能性,是否能判断自己添加的条件的合理性。预案:1、AB=AC(SAS)2、BD=CE(SAS)3、∠B=∠C...