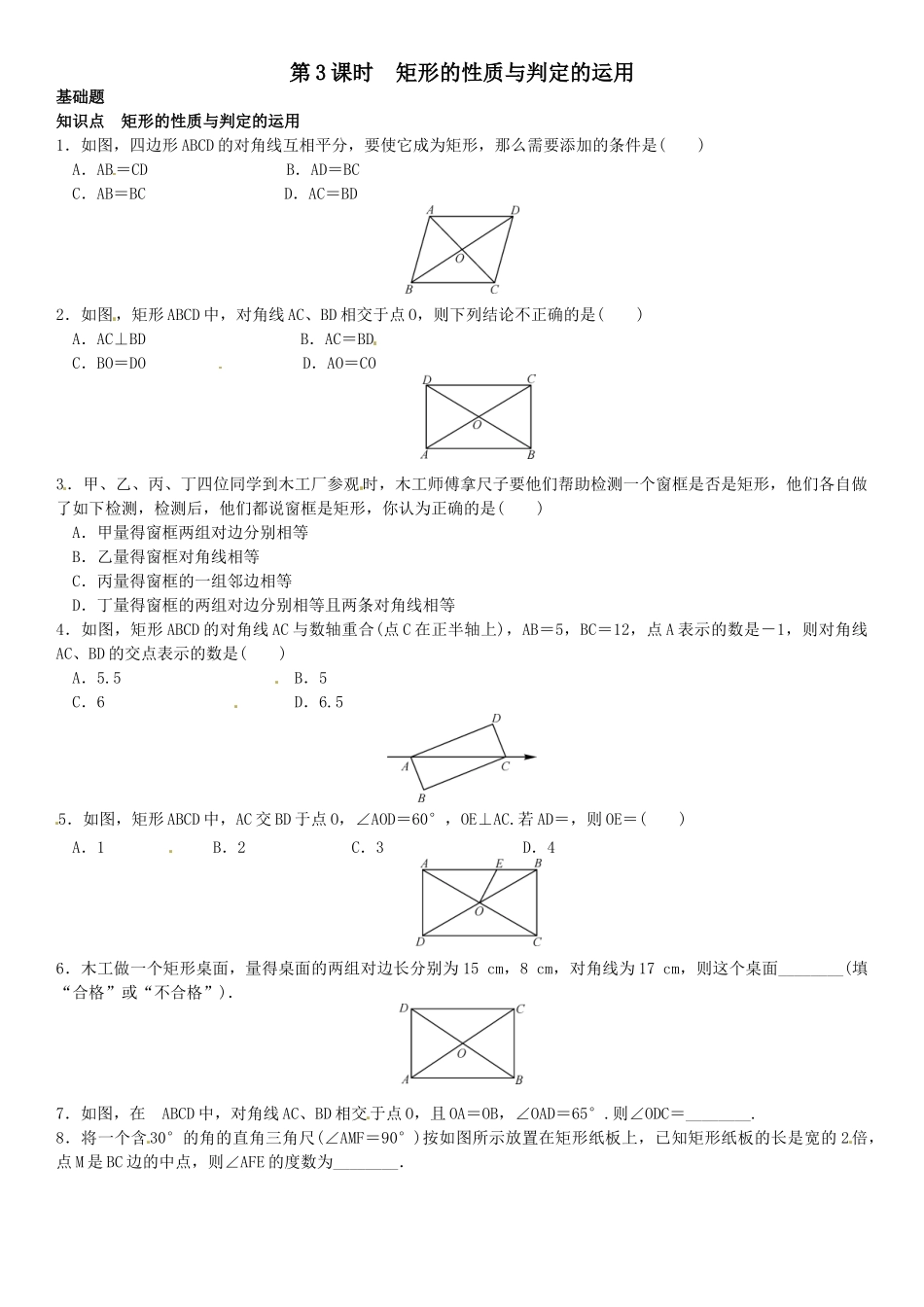
第3课时矩形的性质与判定的运用基础题知识点矩形的性质与判定的运用1.如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是()A.AB=CDB.AD=BCC.AB=BCD.AC=BD2.如图,矩形ABCD中,对角线AC、BD相交于点O,则下列结论不正确的是()A.AC⊥BDB.AC=BDC.BO=DOD.AO=CO3.甲、乙、丙、丁四位同学到木工厂参观时,木工师傅拿尺子要他们帮助检测一个窗框是否是矩形,他们各自做了如下检测,检测后,他们都说窗框是矩形,你认为正确的是()[来源:Zxxk.Com]A.甲量得窗框两组对边分别相等[来源:学_科_网Z_X_X_K]B.乙量得窗框对角线相等C.丙量得窗框的一组邻边相等D.丁量得窗框的两组对边分别相等且两条对角线相等4.如图,矩形ABCD的对角线AC与数轴重合(点C在正半轴上),AB=5,BC=12,点A表示的数是-1,则对角线AC、BD的交点表示的数是()A.5.5B.5C.6D.6.55.如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=,则OE=()A.1B.2C.3D.46.木工做一个矩形桌面,量得桌面的两组对边长分别为15cm,8cm,对角线为17cm,则这个桌面________(填“合格”或“不合格”).7.如图,在ABCD中,对角线AC、BD相交于点O,且OA=OB,∠OAD=65°.则∠ODC=________.8.将一个含30°的角的直角三角尺(∠AMF=90°)按如图所示放置在矩形纸板上,已知矩形纸板的长是宽的2倍,点M是BC边的中点,则∠AFE的度数为________.9.(海南中考)如图,矩形ABCD中,AB=3,BC=4,则图中四个小矩形的周长之和为________.10.如图,在Rt△ABC中,∠ACB=90°,DE、DF是△ABC的中位线,连接EF、CD.求证:EF=CD.中档题11.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快________s后,四边形ABPQ成为矩形.12.如图所示,ABCD中,AQ,BN,CN,DQ分别是∠DAB,∠ABC,∠BCD,∠CDA的平分线,AQ与BN交于P,CN与DQ交于M,在不添加其他条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程.(要求:推理过程中要用到“平行四边形”和“角平分线”这两个条件)[来源:学科网ZXXK]综合题13.如图,已知在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连接EF,M为EF的中点.(1)请判断四边形PECF的形状,并说明理由;[来源:Z.xx.k.Com](2)随着P点在边AB上位置的改变,CM的长度是否也会改变?若不变,请你求CM的长度;若有变化,请你求CM的变化范围.参考答案10.D2.A3.D4.A5.A6.合格7.25°8.15°9.1410.证明:∵DE、DF是△ABC的中位线,∴DE∥BC,DF∥AC.∴四边形DECF是平行四边形.又∵∠ACB=90°,∴四边形DECF是矩形.∴EF=CD.11.4[来源:学*科*网]12.结论:四边形PQMN是矩形.理由如下:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠BAD+∠ABC=180°.又∵AQ,BN分别是∠BAD,∠ABC的角平分线,∴∠PBA=∠ABC,∠PAB=∠BAD.∴∠PBA+∠PAB=(∠ABC+∠BAD)=×180°=90°.∴∠APB=90°.同理:∠BNM=∠AQD=90°.∴四边形PQMN是矩形.13.(1)四边形PECF是矩形.理由如下:在△ABC中,AC=3,BC=4,AB=5,∴AC2+BC2=32+42=52=AB2.∴∠ACB=90°.∵PE⊥AC,PF⊥BC,∴∠PEC=∠ACB=∠CFP=90°.∴四边形PECF是矩形.(2)CM的长度会改变.理由:连接PC,由(1)证得四边形PECF是矩形,∵M是EF的中点,∴M在PC上且EF=PC,CM=PC.过点C作CD⊥AB,当CD=PC时PC最小,此时PC===2.4.∵点P在斜边AB上(不与A、B重合),∴PC<BC=4.∴PC的范围是2.4≤PC<4,即EF的范围是2.4≤EF<4.∴CM的范围是1.2≤CM<2.不用注册,免费下载!