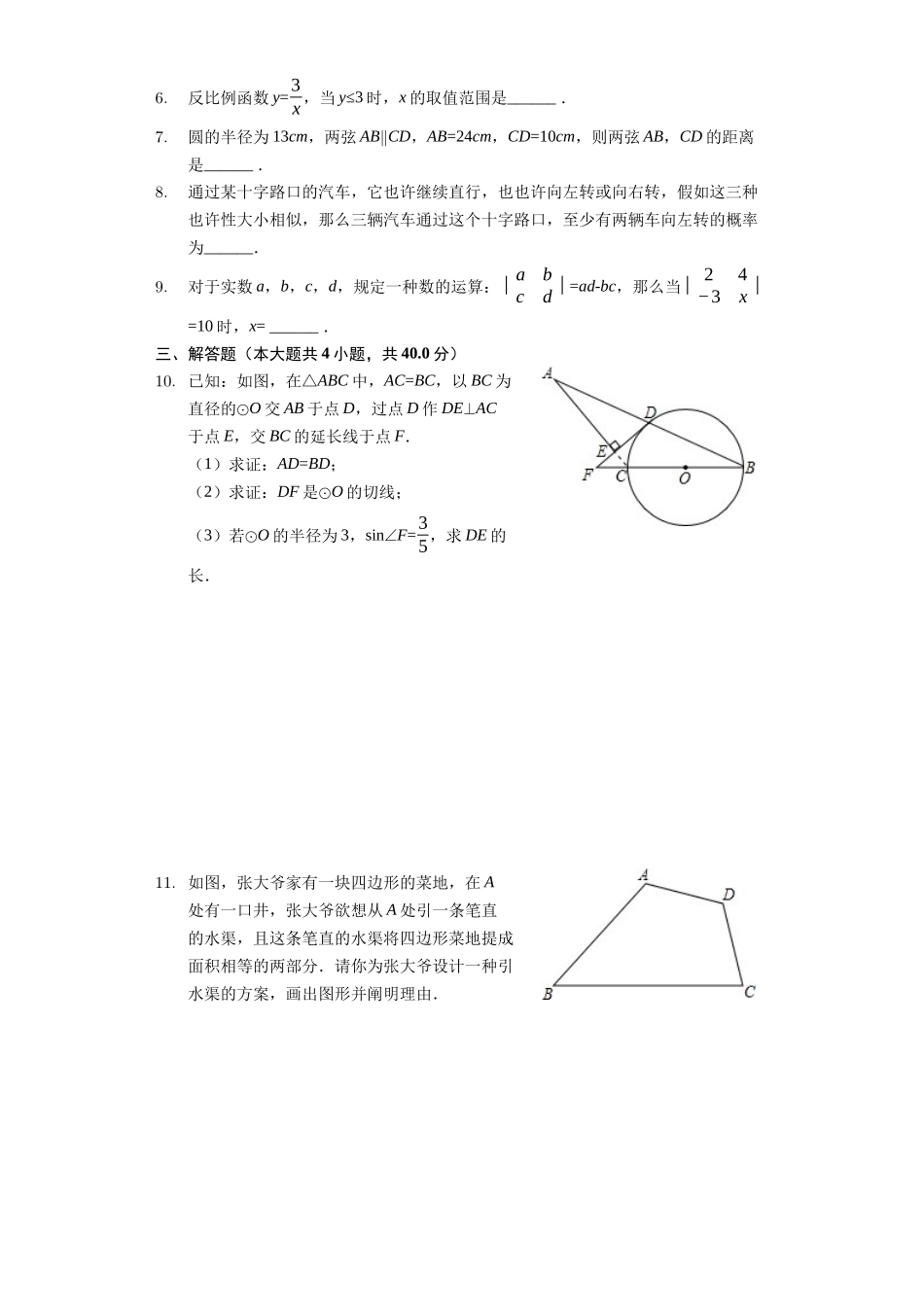
浙江省温州市自主招生数学试卷一、选择题(本大题共5小题,共20.0分)1.实数a,b在数轴上对应的点的位置如图,则必有()A.ab<0B.ab>0C.a−∨b∨¿0D.a+b>02.无论m为何实数,直线y=2x+m与直线y=-x+3的交点都不也许在()A.第一象限B.第二象限C.第三象限D.第四象限3.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中对的的结论有()A.2个B.3个C.4个D.5个4.假如外切的两圆⊙O1和⊙O2的半径分别为2和4,那么半径为6,与⊙O1和⊙O2都相切的圆有()A.4个B.5个C.6个D.7个5.如图,从A点沿线段走到B点,规定每一步都是向右或向上,则走法共有()A.9种B.16种C.20种D.25种二、填空题(本大题共4小题,共20.0分)6.反比例函数y=3x,当y≤3时,x的取值范围是______.7.圆的半径为13cm,两弦AB∥CD,AB=24cm,CD=10cm,则两弦AB,CD的距离是______.8.通过某十字路口的汽车,它也许继续直行,也也许向左转或向右转,假如这三种也许性大小相似,那么三辆汽车通过这个十字路口,至少有两辆车向左转的概率为______.9.对于实数a,b,c,d,规定一种数的运算:∣abcd∣=ad-bc,那么当∣24−3x∣=10时,x=______.三、解答题(本大题共4小题,共40.0分)10.已知:如图,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.(1)求证:AD=BD;(2)求证:DF是⊙O的切线;(3)若⊙O的半径为3,sin∠F=35,求DE的长.11.如图,张大爷家有一块四边形的菜地,在A处有一口井,张大爷欲想从A处引一条笔直的水渠,且这条笔直的水渠将四边形菜地提成面积相等的两部分.请你为张大爷设计一种引水渠的方案,画出图形并阐明理由.12.小亮上午从家里出发匀速步行去上学,小亮的妈妈在小亮出发后10分钟,发现小亮的数学书本没带,于是她带上书本立即匀速骑车按小亮上学的路线追赶小亮,成果与小亮同步抵达学校.已知小亮在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图象如图中的折线段OA-AB所示.(1)试求折线段OA-AB所对应的函数关系式;(2)请解释图中线段AB的实际意义;(3)请在所给的图中画出小亮的妈妈在追赶小亮的过程中,她所在位置与家的距离S(千米)与小亮出发后的时间t(分钟)之间函数关系的图象.(友谊提醒:请对画出的图象用数据作合适的标注)13.已知梯形ABCD中,AD∥BC,且AD<BC,AD=5,AB=DC=2.(1)如图,P为AD上的一点,满足∠BPC=∠A,求AP的长;(2)假如点P在AD边上移动(点P与点A、D不重叠),且满足∠BPE=∠A,PE交直线BC于点E,同步交直线DC于点Q.①当点Q在线段DC的延长线上时,设AP=x,CQ=y,求y有关x的函数关系式,并写出自变量x的取值范围;②当CE=1时,写出AP的长.(不必写解答过程)答案和解析1.【答案】A【解析】解:由数轴可得出:1>a>0,-1<b,A、<0,对的;B、ab<0,故此选项错误;C、a-|b|<0,故此选项错误;D、a+b<0,故此选项错误;故选:A.运用数轴分别得出1>a>0,-1<b,进而分析各选项得出即可.此题重要考察了实数与数轴,得出a,b的取值范围是解题关键.2.【答案】C【解析】解:由于直线y=-x+3的图象不通过第三象限.因此无论m取何值,直线y=2x+m与直线y=-x+3的交点不也许在第三象限.故选C.直线y=-x+3通过第一,二,四象限,一定不通过第三象限,因而直线y=2x+m与直线y=-x+3的交点不也许在第三象限.本题考察了两条直线相交的问题,需注意应找到完整的函数,进而找到它不通过的象限,那么交点就一定不在那个象限.3.【答案】A【解析】解:开口向下,a<0;对称轴在y轴的右侧,a、b异号,则b>0;抛物线与y轴的交点在x轴的上方,c>0,则abc<0,因此①不对的;当x=-1时图象在x轴上,则y=a-b+c=0,即a+c=b,因此②不对的;对称轴为直线x=1,则x=2时图象在x轴上方,则y=4a+2b+c>0,因此③对的;x=-=1,则a=-b,而a-b+c=0,则-b-b+c=0,2c=3b,因此④不对的;开口向下,当x=1,y有最大值a+b+c;当x=m(m≠1)时,y=am2+bm+c,则a+b+c>am2+bm+c,即a+b>m(am+b...