（衡水万卷）高考数学二轮复习 八 立体几何（二）作业 理-人教版高三数学试题VIP免费

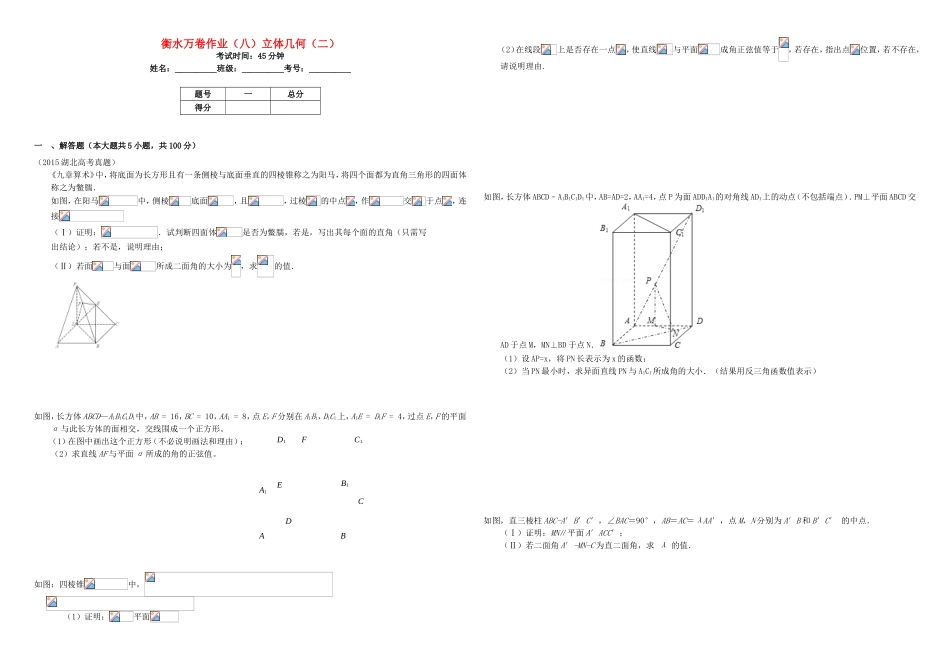
衡水万卷作业（八）立体几何（二）考试时间：45分钟姓名：__________班级：__________考号：__________题号一总分得分一、解答题（本大题共5小题，共100分）（2015湖北高考真题）《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，在阳马中，侧棱底面，且，过棱的中点，作交于点，连接（Ⅰ）证明：．试判断四面体是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；（Ⅱ）若面与面所成二面角的大小为，求的值．如图，长方体ABCD—A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4，过点E，F的平面α与此长方体的面相交，交线围成一个正方形。（1）在图中画出这个正方形（不必说明画法和理由）；（2）求直线AF与平面α所成的角的正弦值。如图：四棱锥中，（1）证明：平面（2）在线段上是否存在一点，使直线与平面成角正弦值等于，若存在，指出点位置，若不存在，请说明理由.如图，长方体ABCD﹣A1B1C1D1中，AB=AD=2，AA1=4，点P为面ADD1A1的对角线AD1上的动点（不包括端点）．PM⊥平面ABCD交AD于点M，MN⊥BD于点N．（1）设AP=x，将PN长表示为x的函数；（2）当PN最小时，求异面直线PN与A1C1所成角的大小．（结果用反三角函数值表示）如图，直三棱柱ABC-A′B′C′，∠BAC＝90°，AB＝AC＝λAA′，点M，N分别为A′B和B′C′的中点．（Ⅰ）证明：MN∥平面A′ACC′；（Ⅱ）若二面角A′-MN-C为直二面角，求λ的值．DD1C1A1EFABCB1衡水万卷作业（八）答案解析一、解答题（解法1）（Ⅰ）因为底面，所以，由底面为长方形，有，而，所以.而，所以.又因为，点是的中点，所以.而，所以平面.而，所以.又，，所以平面.由平面，平面，可知四面体的四个面都是直角三角形，即四面体是一个鳖臑，其四个面的直角分别为.（Ⅱ）如图1，在面内，延长与交于点，则是平面与平面的交线.由（Ⅰ）知，，所以.又因为底面，所以.而，所以.故是面与面所成二面角的平面角，设，，有，在Rt△PDB中,由,得,则,解得.所以故当面与面所成二面角的大小为时，.（解法2）（Ⅰ）如图2，以为原点，射线分别为轴的正半轴，建立空间直角坐标系.设，，则，，点是的中点，所以，，于是，即.又已知，而，所以.因,,则,所以.由平面，平面，可知四面体的四个面都是直角三角形，即四面体是一个鳖臑，其四个面的直角分别为.（Ⅱ）由，所以是平面的一个法向量；由（Ⅰ）知，，所以是平面的一个法向量.若面与面所成二面角的大小为，则，解得.所以故当面与面所成二面角的大小为时，.考点：1.四棱锥的性质，2.线、面垂直的性质与判定，3.二面角.(1)交线圈成的正方形EHGF如图；（2）作EM⊥AB,垂足为M，则AM==4，EM==8.因为EHGF为正方形，所以EH=EF=BC=10.于是MH=,所以AH=10.以D为坐标原点，的方向为x轴正方向，建立如图所示的空间直角坐标系D-xyz，则A(10，0,0),H(10，10，0),E(10，4，8),F(0,4,8),=(10,0,0),,设是平面EHGF的法向量，则即，所以可取又，故.所以AF与平面EHGF所成角的正弦值为。(1)略；(2)存在，F为PD的中点解析：(1）证明：取线段BC中点E，连结AE．因为AD＝，∠PDA=30°，所以PA=1．因为AD∥BC，∠BAD=150°所以∠B=30°．又因为AB=AC，所以AE⊥BC，而BC＝2，所以AC＝AB＝=2，因为PC＝，所以PC2=PA2+AC2，即PA⊥AC．因为PA⊥AD，且AD，AC⊂平面ABCD，AD∩AC=A，所以PA⊥平面ABCD．（2）解：以A为坐标原点，以AE，AD，AP所在直线分别为x，y，z轴，建立空间直角坐标系如图所示，则P(0，0，1),B(1，,,0),处（1，,，0），D(0，,,0)，设，因为点F在线段PD上，设,可得，即，所以，设平面PBC的法向量为，则有，即，令x=1，得，因为直线CF与平面PBC所成角的正弦值等于，所以，解得，所以点F是线段PD的中点．.【思路点拨】证明线面垂直通常利用其判定定理转化为线线垂直进行证明，遇到线面角问题，可建立空间直角坐标系利用空间向量的夹角进行求值.考点：异面直线及其所成的角；函数解析式的求解及常用方法．专题：计算题；函数的性质及应用；空间角．分析：（1）求出PM，AM，运用余弦定理，求得PN；（2）求出PN...