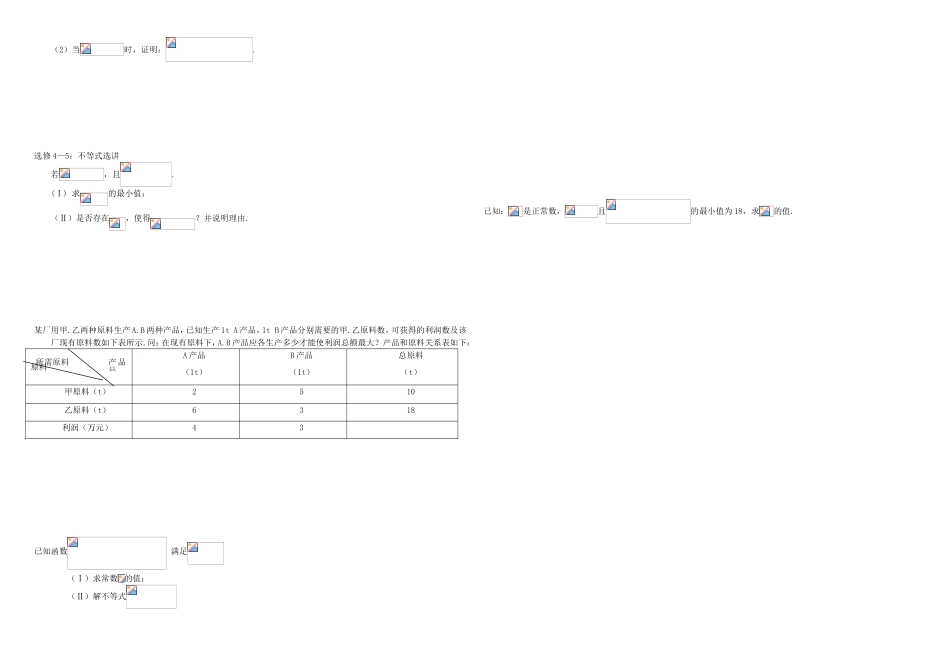
衡水万卷作业周测(二十)理科数学不等式必修+选讲考试时间:120分钟姓名:__________班级:__________考号:__________题号一二三总分得分一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)若,则关于的不等式的解集是()A.B.C.D.不等式的解集是()A.B.C.D.不等式的解集是()A.B.C.D.设满足条件,则的最小值为()A.6B.4C.3D.2(2015•丽水一模)已知实数x,y满足约束条件且目标函数z=2x+y的最大值是6,最小值是1,则的值是()A.1B.2C.3D.4已知实数满足不等式组,则的最大值为()A.3B。4C。6D。9已知变量满足约束条件,则的最大值为()A.8B.11C.9D.12如果,那么下列不等式成立的是()(A)(B)(C)(D)若,则下列不等式中,不能成立的是()A.B.C.D.给关于的不等式提供四个解,①当时,;②当时,;③当时,;④当时,.那么原不等式的解为()A.②或③B.①或③C.①或④D.②或④不等式的解集是()A.B.C.D.若,使不等式在上的解集不是空集,则的取值范围()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)若关于实数的不等式无解,则实数的取值范围是_________若不等式对任意恒成立,则a的取值范围____________若x,y满足约束条件,则的最大值为____________.设x,y满足约束条件:,则z=x+y的最大值_______三、解答题(本大题共6小题,第一题10分,第二题12分。共70分)选修4—5:不等式选讲已知定义在R上的函数的最小值为.(I)求的值;(II)若为正实数,且,求证:.选修4-5:不等式选讲设函数,,记的解集为M,的解集为N.(1)求M;(2)当时,证明:.选修4—5:不等式选讲若,且.(Ⅰ)求的最小值;(Ⅱ)是否存在,使得?并说明理由.某厂用甲.乙两种原料生产A.B两种产品,已知生产1tA产品,1tB产品分别需要的甲.乙原料数,可获得的利润数及该厂现有原料数如下表所示.问:在现有原料下,A.B产品应各生产多少才能使利润总额最大?产品和原料关系表如下:A产品(1t)B产品(1t)总原料(t)甲原料(t)2510乙原料(t)6318利润(万元)43已知函数满足(Ⅰ)求常数的值;(Ⅱ)解不等式已知:是正常数,且的最小值为18,求的值.产品品所需原料原料衡水万卷作业周测(二十)答案解析一、选择题CDB【解析】,用穿根法解得不等式解集为.C【考点】:简单线性规划.【专题】:不等式的解法及应用.【分析】:先根据约束条件画出可行域,再利用目标函数的最值,作用平面区域即可得到结论..【解析】:解:由题意得:作出目标函数2x+y=6,和2x+y=1,则对应的平面区域如图:则B,C在直线ax+by+c=0上,由,解得,即C(1,﹣1),由,解得,即B(2,2),则B,C在直线在直线ax+by+c=0上,∴BC的方程为3x﹣y﹣4=0,即a=3,b=﹣1,c=﹣4,则=4,故选:D【点评】:本题主要考查了简单的线性规划,以及利用几何意义求最值的方法.【答案】C【解析】作出不等式组所对应的可行域(如图阴影),变形目标函数z=2x+y可得y=-2x+z,平移直线y=-2x可知,当直线经过点A(3,0)时,z取最大值,代值计算可得z=2x+y的最大值为6【思路点拨】作出可行域,平行直线可得直线过点A(3,0)时,z取最大值,代值计算可得.B解析:画出可行域,平移目标函数得最优解为直线y=2与x-y=1的交点(3,2)所以的最大值为11,故选B.【思路点拨】画出可行域,平移目标函数确定最优解即可.D思路分析:本题主要考查不等式的性质,必须透彻理解不等式性质的条件和结论,在应用不等式性质时,注意看性质条件是否具备,做到有根有据,这样才能正确.合理找到答案。方法一:。将两边同乘以,可得,,这与已知条件矛盾,故选B.BB【解析】解法1:排除法,将代入原不等式,不成立,排A;将代入原不等式,不成立,排除C,D.故选B.解法2:不等式等价于即解得所以不等式的解集为或.C二、填空题【解析】由于,所以只需即可【答案】【解析】画出可行域,如图所示,将目标函数变形为,当z取最大时,直线的纵截距最大,故将直线尽可能地向上平移到,则的最大值为。xy–1–2–3–41234–1–2–3–41234DCBO.三、解答题选修:不等式选讲本小题主要考查绝对值不等式、柯西不等式等基础知识...