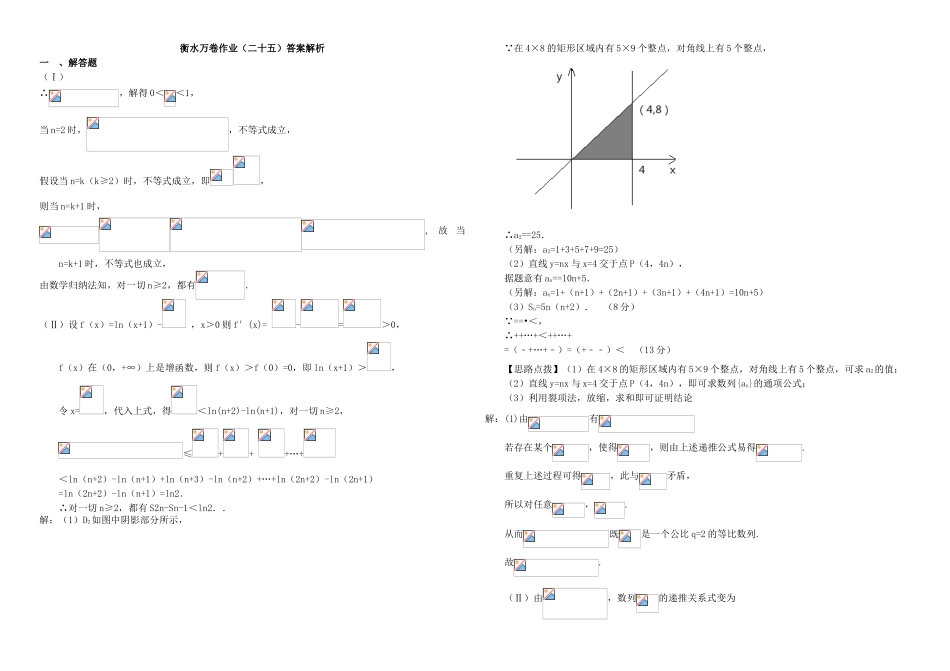
衡水万卷作业(二十五)数列综合题(一)考试时间:45分钟姓名:__________班级:__________考号:__________题号一总分得分一、解答题(本大题共5小题,共100分)设数列各项均为正数,且满足.(I)求证:对一切n≥2,都有(II)已知前n项和为,求证:对一切n≥2,都有.设不等式组所表示的平面区域,记内整点的个数为(横纵坐标均为整数的点称为整点)。(1)时,先在平面直角坐标系中做出平面区域,在求的值;(2)求数列的通项公式;(3)记数列的前n项和为,试证明:对任意,恒有成立。(2015重庆高考真题)在数列中,(I)若求数列的通项公式;(II)若证明:已知首项大于的等差数列的公差,且.(1)求数列的通项公式;(2)若数列满足:,,,其中.①求数列的通项;②是否存在实数,使得数列为等比数列?若存在,求出的值;若不存在,请说明理由.设数列的前n项和为.若对任意的正整数n,总存在正整数m,使得,则称是“H数列”.(1)若数列的前n项和,证明:是“H数列”;(2)设是等差数列,其首项,公差.若是“H数列”,求d的值;(3)证明:对任意的等差数列,总存在两个“H数列”和,使得成立.衡水万卷作业(二十五)答案解析一、解答题(Ⅰ)∴,解得0<<1,当n=2时,,不等式成立,假设当n=k(k≥2)时,不等式成立,即,则当n=k+1时,,故当n=k+1时,不等式也成立,由数学归纳法知,对一切n≥2,都有.(Ⅱ)设f(x)=ln(x+1)-,x>0则f′(x)=-=>0,f(x)在(0,+∞)上是增函数,则f(x)>f(0)=0,即ln(x+1)>,令x=,代入上式,得<ln(n+2)-ln(n+1),对一切n≥2,≤+++…+<ln(n+2)-ln(n+1)+ln(n+3)-ln(n+2)+…+ln(2n+2)-ln(2n+1)=ln(2n+2)-ln(n+1)=ln2.∴对一切n≥2,都有S2n-Sn-1<ln2..解:(1)D2如图中阴影部分所示,∵在4×8的矩形区域内有5×9个整点,对角线上有5个整点,∴a2==25.(另解:a2=1+3+5+7+9=25)(2)直线y=nx与x=4交于点P(4,4n),据题意有an==10n+5.(另解:an=1+(n+1)+(2n+1)+(3n+1)+(4n+1)=10n+5)(3)Sn=5n(n+2).(8分)∵==•<,∴++…+<++…+=(﹣+…+﹣)=(+﹣﹣)<(13分)【思路点拨】(1)在4×8的矩形区域内有5×9个整点,对角线上有5个整点,可求a2的值;(2)直线y=nx与x=4交于点P(4,4n),即可求数列{an}的通项公式;(3)利用裂项法,放缩,求和即可证明结论解:(1)由有若存在某个,使得,则由上述递推公式易得.重复上述过程可得,此与矛盾,所以对任意,.从而既是一个公比q=2的等比数列.故.(Ⅱ)由,数列的递推关系式变为变形为.由上式及归纳可得因为,所以对求和得.另一方面,由上已证的不等式知得.综上,.【答案】(1)(2)①②1【解析】(1)数列的首项,公差,,,2,整理得解得或(舍去).因此,数列的通项.(2)①,.令,则有,.当时,,.因此,数列的通项.②,,,若数列为等比数列,则有,即,解得或.当时,,不是常数,数列不是等比数列,当时,,,数列为等比数列.所以,存在实数使得数列为等比数列.【思路点拨】,则,,.求出通项,当时,,不是常数,数列不是等比数列,当时,,,数列为等比数列.所以,存在实数使得数列为等比数列.(1)当时,当时,∴时,,当时,∴是“H数列”(2)对,使,即取得,∵,∴,又,∴,∴(3)设的公差为d令,对,,对,则,且为等差数列的前n项和,令,则当时;当时;当时,由于n与奇偶性不同,即非负偶数,因此对,都可找到,使成立,即为“H数列”.的前n项和,令,则∵对,是非负偶数,∴即对,都可找到,使得成立,即为“H数列”因此命题得证.