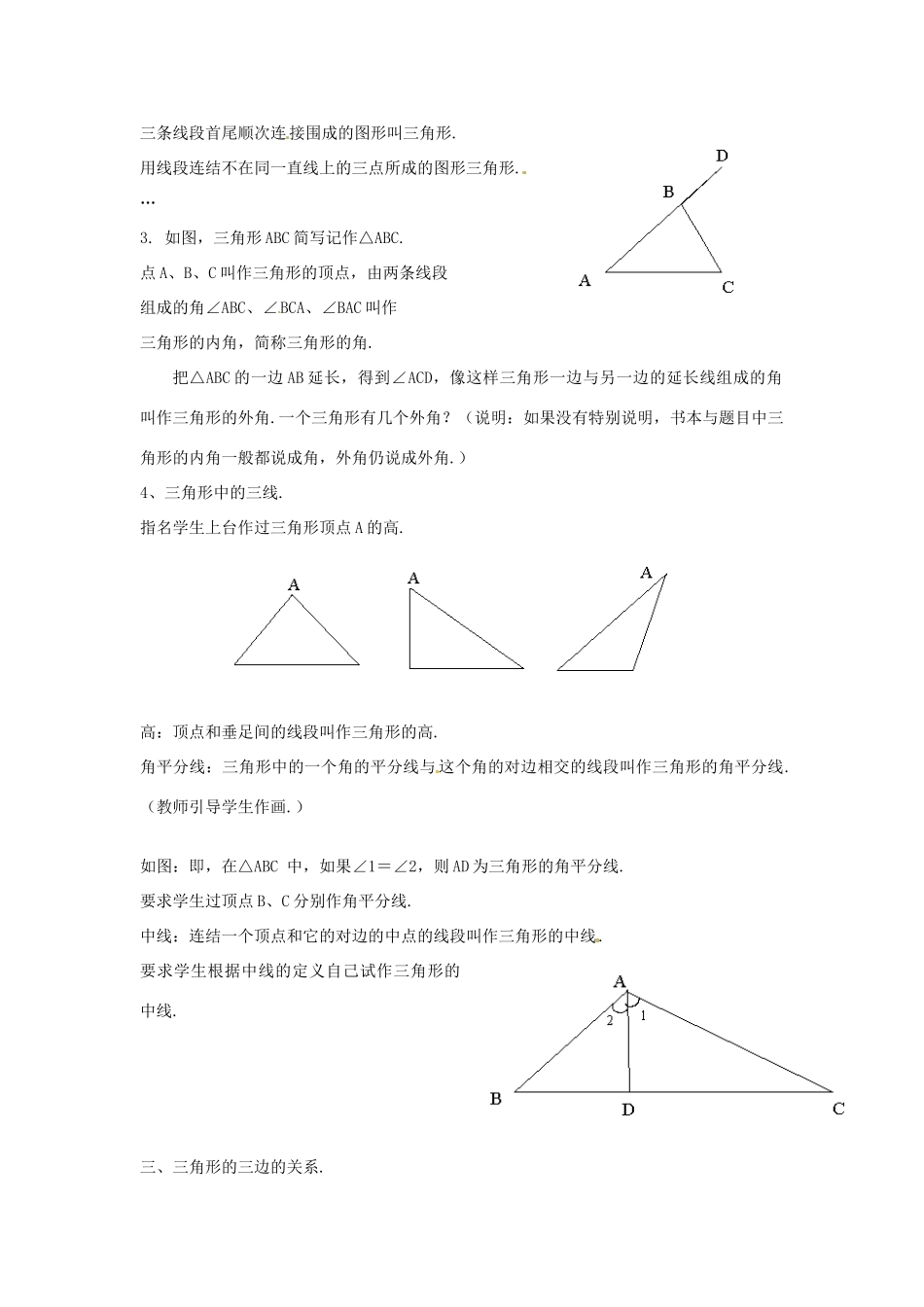
5.3三角形-5.4三角形的内角和目的要求:1.认识三角形的有关概念.2.认识并能够画出三角形的中线、角平分线、高.3.理解三角形的三边的关系.4.认识三角形的内外角和,并进行有关应用.重点:1.三角形的有关概念.2.三角形的内外角和.准备:作图工具、小黑板、幻灯过程:一、复习.(幻灯)1.什么是轴对称图形.2.李村与王村同在一小河的一侧,如图,村上计划在小河边修建一个水站,同时供水给李村与王村.你能帮村上设计一条线路,使修建费用最少?3.有一块三角形的废木料,如图,请你在这块木料中截取一个最大的圆.二、三角形的有关概念.1.请同学回顾小学所学的三角形是怎样下定义的?用你自己的话说说什么是三角形.(让学生自由发挥)2.小结三角形的定义:三条线段首尾顺次连接围成的图形叫三角形.用线段连结不在同一直线上的三点所成的图形三角形.…3.如图,三角形ABC简写记作△ABC.点A、B、C叫作三角形的顶点,由两条线段组成的角∠ABC、∠BCA、∠BAC叫作三角形的内角,简称三角形的角.把△ABC的一边AB延长,得到∠ACD,像这样三角形一边与另一边的延长线组成的角叫作三角形的外角.一个三角形有几个外角?(说明:如果没有特别说明,书本与题目中三角形的内角一般都说成角,外角仍说成外角.)4、三角形中的三线.指名学生上台作过三角形顶点A的高.高:顶点和垂足间的线段叫作三角形的高.角平分线:三角形中的一个角的平分线与这个角的对边相交的线段叫作三角形的角平分线.(教师引导学生作画.)如图:即,在△ABC中,如果∠1=∠2,则AD为三角形的角平分线.要求学生过顶点B、C分别作角平分线.中线:连结一个顶点和它的对边的中点的线段叫作三角形的中线.要求学生根据中线的定义自己试作三角形的中线.三、三角形的三边的关系.1.动手操作.给你三条长为:2cm、3cm、6cm的线段,请动用所有的作图工具,并与同学进行探讨,画出一个三角形,且三角形的三边的长正好为2cm、3cm、6cm(要求画实际大小)让学生发现它的不可能性.给你2cm、3cm、5cm的线段行不行?给你2cm、3cm、4cm的线段行不行?2.小结得到:三角形任意两边的和大于第三边.三角形任意两边的的差小于第三边.3.用图形说明.如图:AB+BC>ACAB+AC>BCAC+BC>ABAC-BC<ABAC-AB<BCAB-BC<AC4.快速判断下列给出的三边能否组成三角形?为什么?⑴6cm、8cm、11cm(幻灯)⑵5.5m、3.2m、2m⑶、3cm、4cm、5cm⑷、54cm、68cm、13dm5、拓展.(小黑板)⑴、现如果有4cm、8cm两根木棍,想再找一根木棍与已有的木棍拼成三角形.找的这根木棍多长符合要求?⑵、现有4cm、5cm两根木棍,想再找一根木棍与已有的木棍拼成等腰三角形.找的这根木棍多长符合要求?四、三角形的内外角和.1.动手操作.作任意△ABC,用量角器测量这个三角形的每一个内角,再计算三个内角的和是多少?与同学交流.(三个内角之和为180°)2.你能设法证明你的结论吗?(让学生参考书本P131有关知识进行探讨,鼓励学生用不同的方式进行证明.)如:过外角顶点D作平行线向内作三角形两边的平分线交第三边于D把三角形三个内角向一边上的中点D折叠3.利用三角形的内角和,求多边形的内角和.(小黑板)由此得到:多边形内角和=180°(n-2)4.如图:从上面我们可以知:∠ACD=∠A+∠B四边形五边形六边形三角形的一个外角等于和它不相邻的两个内角的和.三角形的一个外角大于任何一个和它不相邻的内角.置疑:哪么一个三角形的三个外角的和是多少?你能证明吗?(提示:利用三角形的一个外角等于和它不相邻的两个内角的和.)要求学生自己进行证明.教师小结:三角形外角和为360°.课后思考:一个n边形的外角和是多少?五、三角形的种类划分.1.小学我们学过哪些三角形?它们都是怎样下定义的?2.在初中我们把锐角三角形和钝角三角形合称斜三角形.3.在初中直角三角形我们用“Rt△”来简写表示.直角所对边叫作斜边.夹直角的两边叫作直角边.如图:在Rt△ABC中,∠C=90°,则AB为斜边.BC、AC这直角边.∵∠A+∠B=180°-∠C=90°∴∠A与∠B互余.直角三角形的两个锐角互为余角.4.两直角边相等的直角三角形叫等腰直角三角形.六、作业.1.P132练习.2.P135A组T1T2.七、小结.