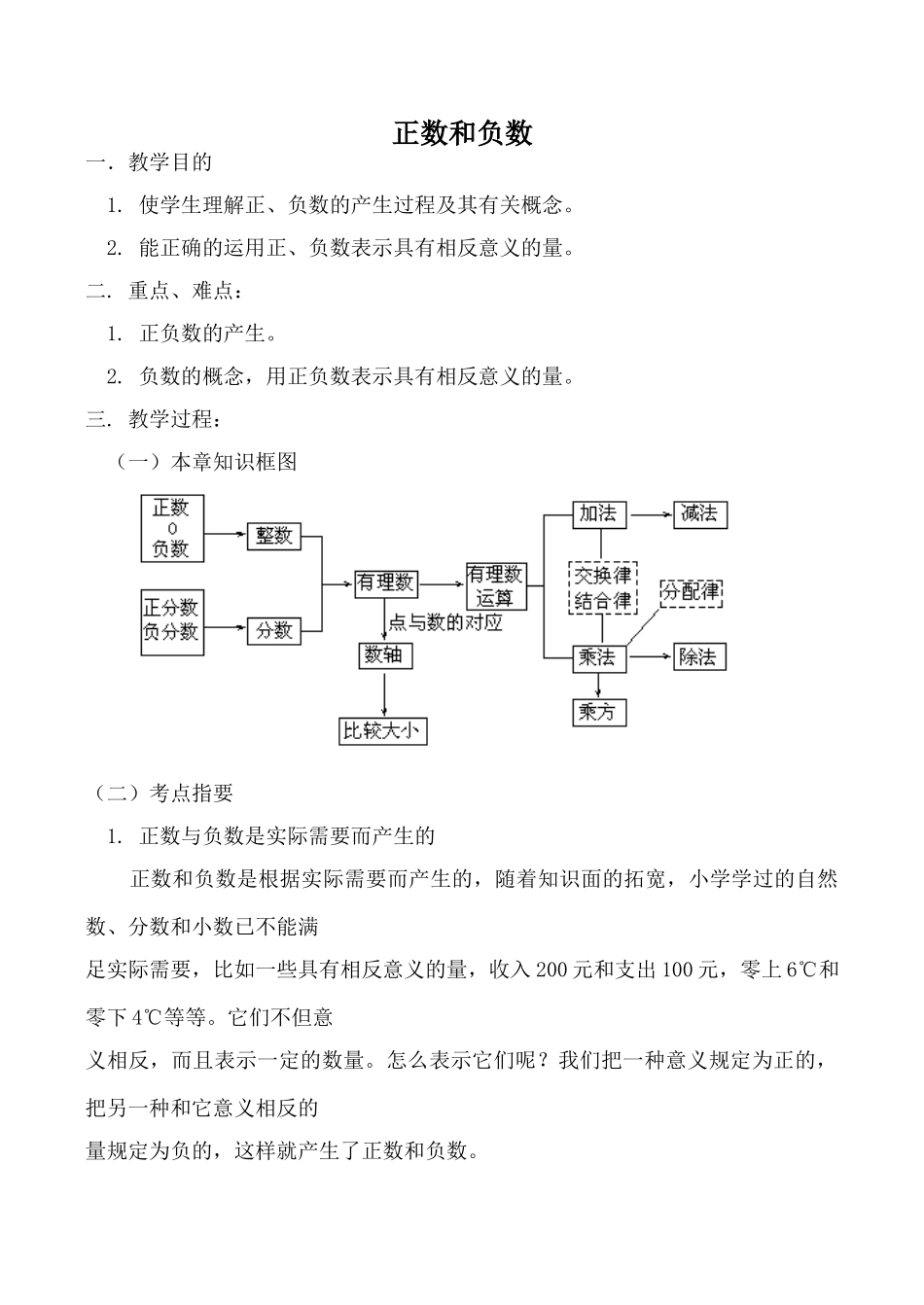
正数和负数一.教学目的1.使学生理解正、负数的产生过程及其有关概念。2.能正确的运用正、负数表示具有相反意义的量。二.重点、难点:1.正负数的产生。2.负数的概念,用正负数表示具有相反意义的量。三.教学过程:(一)本章知识框图(二)考点指要1.正数与负数是实际需要而产生的正数和负数是根据实际需要而产生的,随着知识面的拓宽,小学学过的自然数、分数和小数已不能满足实际需要,比如一些具有相反意义的量,收入200元和支出100元,零上6℃和零下4℃等等。它们不但意义相反,而且表示一定的数量。怎么表示它们呢?我们把一种意义规定为正的,把另一种和它意义相反的量规定为负的,这样就产生了正数和负数。2.正数和负数的概念(1)象5,……这样的数叫正数。如等都是正数。在正数前面加上“-”(读作负)号的数叫做负数。如等都是负数。(2)零既不是正数也不是负数,它表示正数和负数的分界。3.有理数的有关概念(1)整数和分数统称为有理数。注意:整数也可以看成分母为1的分数,但为了研究方便,本章中分数就是指不包括整数的分数。(2)整数包括正整数、零、负整数。(3)分数包括正分数和负分数。4.有理数分类(1)按正数、负数和0的关系分类:(2)按整数和分数的关系分类:【典型例题】例1.说明下列语句的实际意义。(1)温度上升℃(2)运进吨化肥(3)向东走了米(4)盈利元解析:正确理解“-”号的意义是表示相反意义,因此上升℃,实际是下降3℃。解:(1)温度下降3℃;(2)运出200吨化肥;(3)向西走了60米;(4)亏损了15000元。例2.某人月收入1800元表示为1800元,那么每月支出350元应该怎样表示?解析:收入与支出是互为相反意义的量,收入1800元用+1800元表示,支出应用元表示。解:每月支出350元表示为元例3.把下列各数填在相应的集合内。整数集合:{……}负数集合:{……}分数集合:{……}非负数集合:{……}正有理数集合:{……}负分数集合:{……}解析:(1)集合是指具有某一特征的一类事物的全体,注意不要漏掉数0,题目中只是具体的几个符合条件的数,只是一部分,所以通常要加省略号。(2)非负数表示不是负数的所有有理数,应为正数和零,那么非正数表示什么呢?(答:负数和零)答案:整数集合:{……}负数集合:{……}分数集合:{……}非负数集合:{……}正有理数集合:{……}负分数集合:{……}例4.判断题。(1)一个数不是正数就是负数。()(2)海拔米表示比海平面低155米。()(3)温度0℃就是没有温度。()(4)零是最小的有理数。()(5)零是正数。()解析:本题能很好的考查对概念的掌握。解:(1)×;(2)√;(3)×;(4)×;(5)×