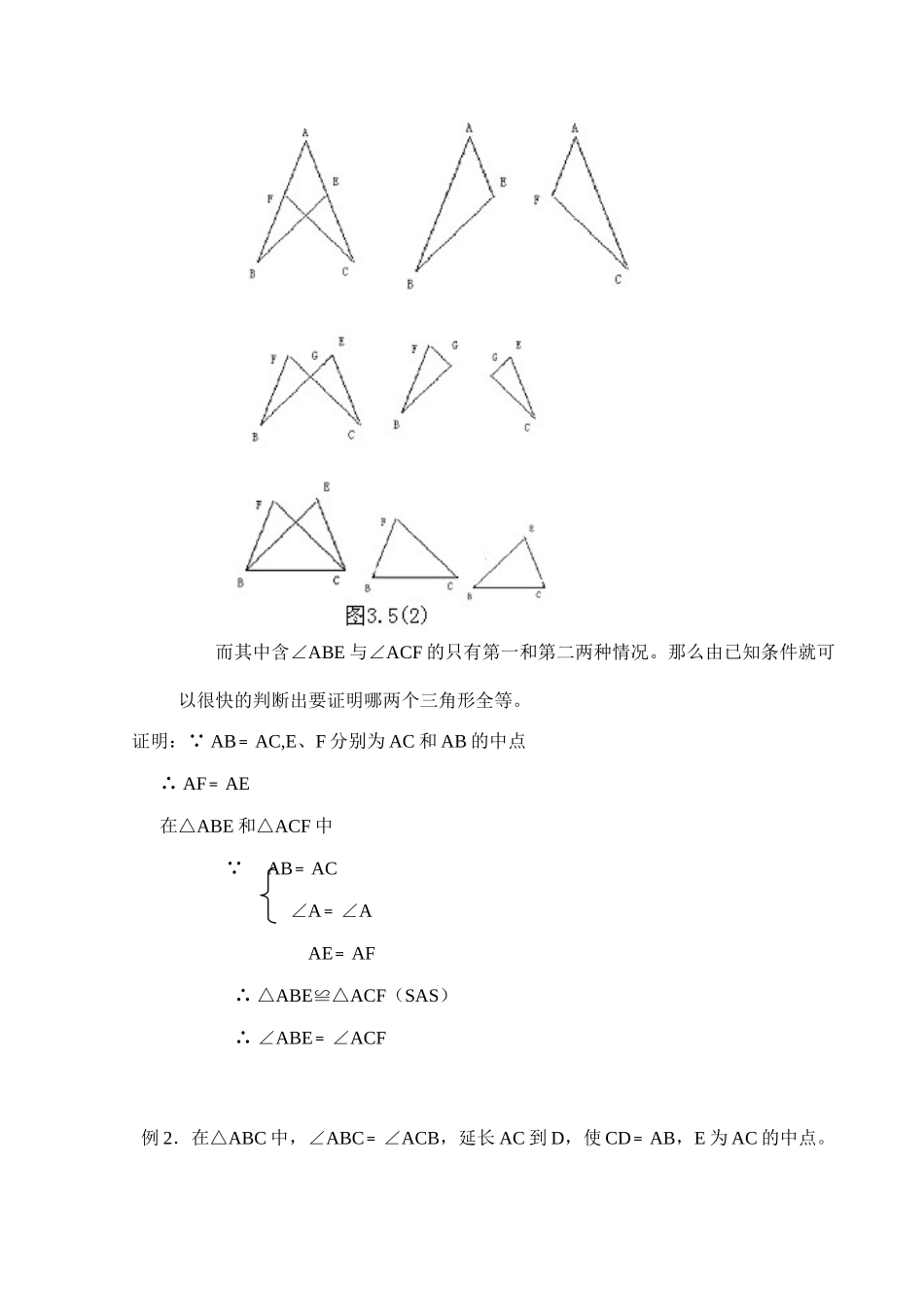
三角形全等的判定(一)2教学目标1.比较熟练地应用边角边公理,进一步培养学生的逻辑推理能力.2.利用三角形全等来证明线段相等或角相等或直线的平行、垂直关系,解决简单的实际问题.3.进一步掌握证明三角形全等问题的规范书写格式.教材分析教学重点:边角边公理的应用.教学难点:准确理解边角边公理的内容,熟练的证明三角形全等.教学过程1.提问“边角边”公理的内容。2.如何判断两个三角形全等?例1.如图3.5(1),已知△ABC中,AB﹦AC,E、F分别是AC和AB的中点。求证:∠ABE﹦∠ACF。分析:要证明两个角相等,常用的方法就是找到含有∠ABE与∠ACF的两个三角形全等即可而在比较复杂的图形中分析出基本图形,找到全等三角形与它们的对应顶点、对应角和对应边又是十分重要的。如图3.5(2),可以找到三对可能全等的三角形。而其中含∠ABE与∠ACF的只有第一和第二两种情况。那么由已知条件就可以很快的判断出要证明哪两个三角形全等。证明:∵AB﹦AC,E、F分别为AC和AB的中点∴AF﹦AE在△ABE和△ACF中∵AB﹦AC∠A﹦∠AAE﹦AF∴△ABE≌△ACF(SAS)∴∠ABE﹦∠ACF例2.在△ABC中,∠ABC﹦∠ACB,延长AC到D,使CD﹦AB,E为AC的中点。求证:2BE﹦BD分析:要证明两条线段相等,常用的方法就是找到含有要证相等的两条线段2BE和BD所在的两个三角形全等即可。观察图形,BD所在三角形为△BCD,而没有2BE合适的三角形,因此需要添加辅助线,构造含有2BE并且和△BCD可能全等的三角形。分析已知条件:BE是△ABC的中线,把BE延长到F,使BF﹦2BE,这样就把原来证2BE﹦BD转化为证BF﹦BD,连接CF,也就是要证△BCD≌△BCF了。这种方法也称做“加倍法”。证明:延长BE到F,使BF﹦2BE,连接CF,在△ABE与△CFE中,∵BE﹦EF(已作),∠AEB﹦∠CEF(对顶角相等)AE﹦EC(已知),∴△ABE≌△CFE(SAS)∴FC﹦AB,∠A﹦∠ECF(全等三角形对应边、对应角都相等)∵AB﹦CD(已知)∴FC﹦CD(等量代换)又∵∠BCD﹦∠ABC﹢∠A(三角形外角性质)∠BCF﹦∠ACB﹢∠ECF(如图)∠ABC﹦∠ACB(已知)ABCDE图3.5(3)ABCDEF图3.5(4)∠ECF﹦∠A(已证)∴∠BCD﹦∠BCF(等量代换)在△BCD与△BCF中,∵CD﹦CF(已证)∠BCD﹦∠BCF(已证)BC﹦BC(公共边)∴△BCD≌△BCF(SAS)∴BD﹦BF(全等三角形对应边相等)∵2BE﹦BF(已作)2BE﹦BD(等量代换)课堂小结1.判定两个三角形全等,需要知道三对元素对应相等,并且其中至少有一对元素是边.2.判定两个三角形全等的方法(除定义外)有SAS.3.研究问题,既要学会从已知想“可知”的尽可能多的结论,还要从未知的各种可能情况,寻求恰当的解题途径.课堂检测1.如图3.5(5),已知E、F分别是△ABC两边AB和AC的中点,在CE的延长线上取EG﹦CE,在BF的延长线上取FH﹦BF。下列说法错误的是()(A)△AEG≌△BEC≌△BFC≌△HFA(B)△AEG≌△BEC(C)△BFC≌△HFA(D)BC﹦AG﹦AHBCEFGHA图3.5(5)2.如图3.5(6),DO⊥BC,OA﹦OC,OB﹦OD,下列说法正确的是()(A)∠B﹦∠C(B)∠B﹢∠D﹦90°(C)∠D﹦∠BAO(D)∠D﹢∠BAO﹦90°3.如图3.5(7),AD﹦AE,AB﹦AC,∠A﹦400,∠B﹦300,则∠EFC的度数为____。4.如图3.5(8),已知D是BC的中点,AD⊥BC于D,P在AD上,则图中全等的三角形有__对。5.如图3.5(9),已知AB﹦AC,AD﹦AE,∠DAE﹦∠BAC。则图中一定全等的三角形是_______6.如图,B、C、E、F是一直线,BE﹦CF,AB﹦DF,AB⊥BC于B,DF⊥EF于F。求证:(1)AB∥DF;(2)AC∥DE;(3)AC﹦DEDACOB图3.5(6)AFBCDE图3.5(7)ABCPD图3.5(8)ADECB图3.5(9)DFECAB图3.5(10)