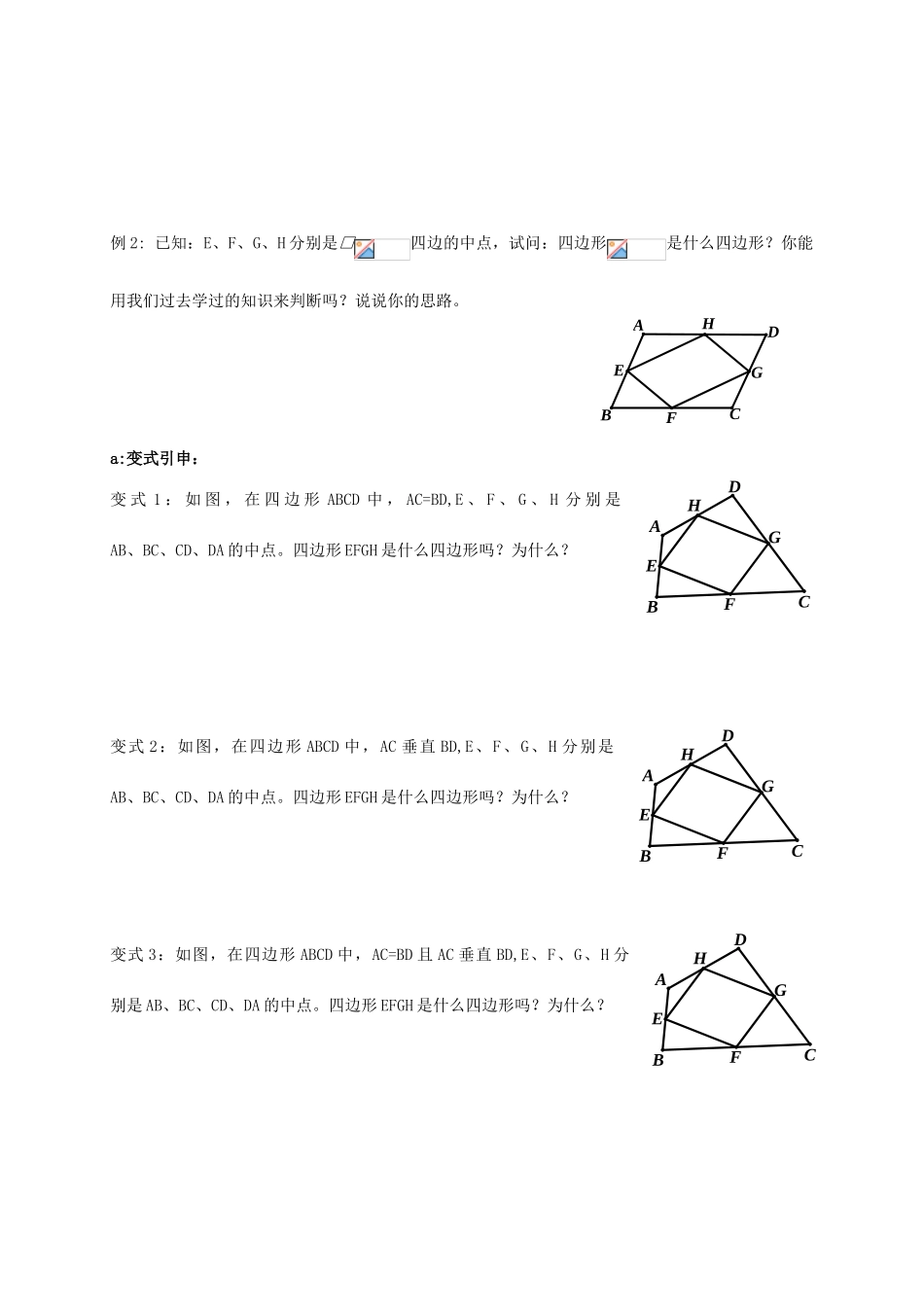
三角形的中位线学习目标:1.探索并掌握三角形中位线的概念、性质;2.会利用三角形的中位线的性质解决有关问题;3.经历探索三角形中位线性质的过程,体会转化的思想方法.学习重点:会利用三角形的中位线的性质解决有关问题.学习难点:经历探索三角形中位线性质的过程,体会转化的思想方法.学习过程:课前准备1、连接三角形两边的线段叫做三角形的2、三角形的中位线,并且等于3、如果一个三角形的面积为8cm2,那么它有条中位线,这些中位线所围成的三角形的面积为_______cm2.4、如果四边形ABCD的四边中点依次是E、F、G、H,那么四边形EFGH是____形.如果AC=24cm,BD=32cm,那么四边形EFGH的周长等于______cm;探索新知1、情境创设:怎样将一张三角形纸片剪成两部分,使分成的两部分能拼与一个平行四边形?2、动手操作(1)、剪一个三角形记为△ABC;(2)、分别取AB、AC的中点D、E,连接DE;(3)、沿DE将△ABC剪成两部分,将△ADE绕点E旋转180°,得四边形BCFD,如图ⅠCEDEDABCBAF观察:四边形BCFD是平行四边形吗?3、新知归纳概念:三角形中位线:性质:三角形中位线性质:AD=DB、AE=EC,DE∥BC且DE=BC从今天开始我们就一起研究这样一条特殊的线段-----三角形的中位线说一说:三角形的中线与三角形的中位线的区别如图:三角形中线是一条连接与对边的线段三角形是一条连接的线段DEDCBACBA知识运用例1.如图,在△ABC中,D是AB上一点,AD=AC,AE平分∠BAC,F是BC的中点,试判断EF与BD的关系,并说明理由。EDABC例2:已知:E、F、G、H分别是□四边的中点,试问:四边形是什么四边形?你能用我们过去学过的知识来判断吗?说说你的思路。a:变式引申:变式1:如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是什么四边形吗?为什么?变式2:如图,在四边形ABCD中,AC垂直BD,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是什么四边形吗?为什么?变式3:如图,在四边形ABCD中,AC=BD且AC垂直BD,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是什么四边形吗?为什么?GFEHADCBGFEHADBCGFEHADCBGFEHADCBb:总结归纳:(1)当例2中四边形ABCD的对角线AC与BD满足条件时,四边形EFGH菱形。(2)当例2中四边形ABCD的对角线AC与BD满足条件时,四边形EFGH矩形。(3)当例2中四边形ABCD的对角线AC与BD满足条件时,四边形EFGH正方形类比:(1)若将例2中“四边形ABCD”改为“平行四边形ABCD”,那么四边形EFGH是形。(2)若将例2中“四边形ABCD”改为“矩形ABCD”,那么四边形EFGH是形。(3)若将例2中“四边形ABCD”改为“菱形ABCD”,那么四边形EFGH是形。(4)若将例2中“四边形ABCD”改为“正方形ABCD”,那么四边形EFGH是形。当堂反馈1、若三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是cm。.2、已知D、E、F是⊿ABC三边的中点。(1)、若⊿DEF的周长是20㎝,则⊿ABC的周长为__________㎝;(2)、图中四个小三角形有何关系:_____________;;3、一个三角形的周长是12cm,面积是8cm2,则这个三角形各边中点围成的三角形的周长是cm,面积为_______cm2。.4、如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E。(1)、若DE的长为36m,求A、B两地间的距离;(2)、如果D、E两点间还有阻隔,你有什么解决办法?EDBCA5、如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,连接EF、EG、FG,那么△EFG是什么三角形?请说明理由.6、如图,在△ABC中,中线BD、CE相交于点O,F、G分别是OB、OC的中点,试判断四边形EFGD的形状,并说明理由.课后作业1、例1中①若四边形ABCD是矩形,则四边形EFGH是形。②若四边形ABCD是菱形,则四边形EFGH是形。2、如图,已知菱形ABCD的对角线相交于点O,E、F分别是AB、AD的中点,试问线段OE与OF有什么关系,并说明理由。3、已知三角形3条中位线的比为3:5:6,三角形的周长是112cm,求三条中位线长。DABCDEF4、如图,在四边形ABCD中,AB=CD,M、N分别是AD、BC的中点,延长BA、NM、CD,分别交于点E、F,试说明:∠BEN=∠NFC(提示:连接BD并...