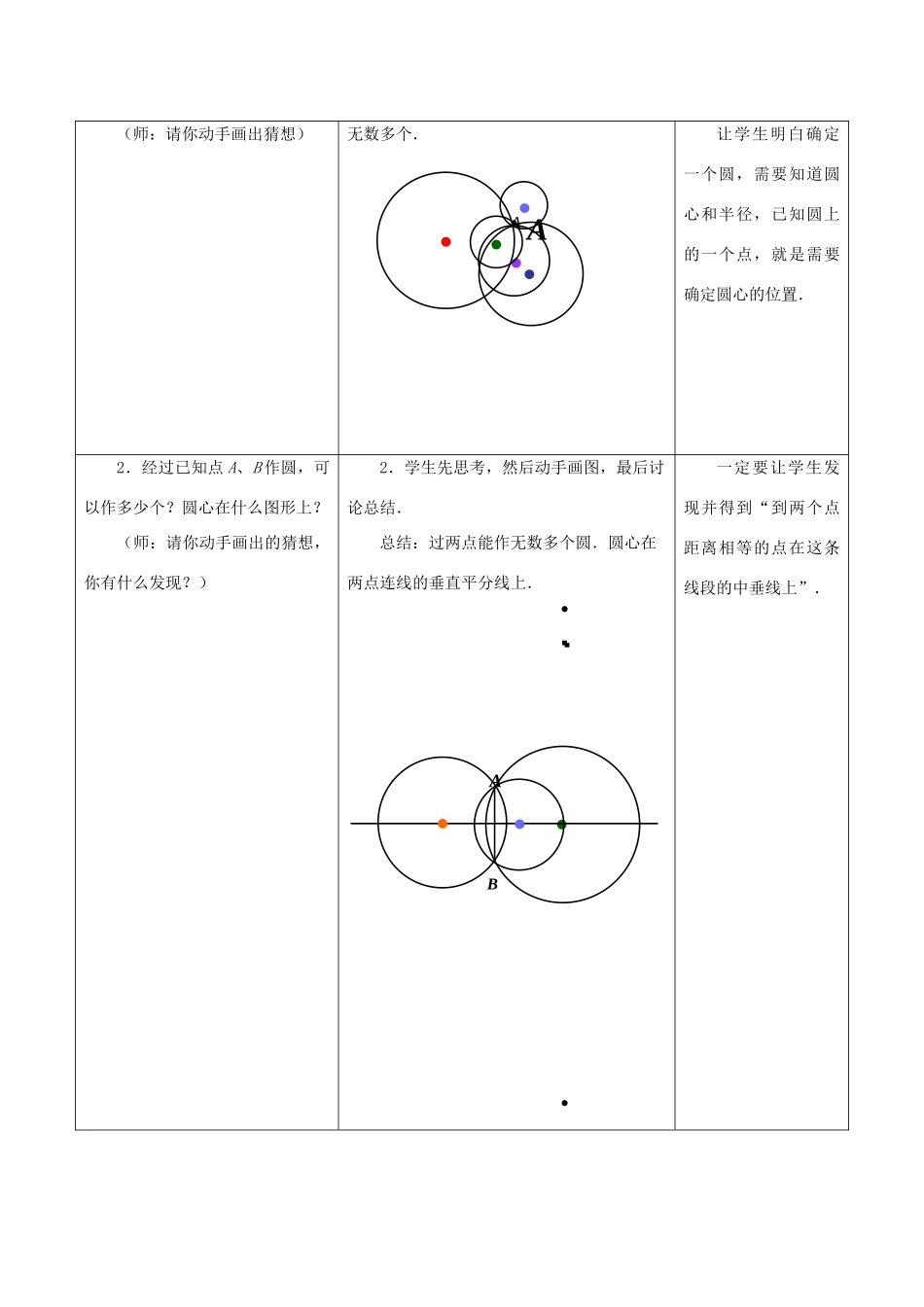
2.3确定圆的条件2.3确定圆的条件教学目标1.经历不在一条直线上的三点确定一个圆的探索过程;2.能够利用尺规,过不在同一直线上的三点画出一个圆;3.了解不在一条直线上的三点确定一个圆,了解三角形的外接圆、三角形的外心、圆的内接三角形的概念,会过不在一条直线上的三点作圆;4.在探究过程中培养学生归纳探索的精神,渗透类比化归的思想.教学重点了解不在一条直线上的三点确定一个圆.教学难点通过类比,经历确定圆的条件的探索过程,说明过不在同一直线上的三点有且只有一个圆.教学过程(教师)学生活动设计思路情境引入考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?先让学生独立思考,然后小组讨论交流.可以引导学生逐步思考.(1)画一个圆需要什么条件:圆心和半径;(2)如何找圆心?利用学生身边的问题创设情境,激发学生的学习兴趣,促进其对“确定圆的条件”的思考.复习回顾(1)过一点可作几条直线?(2)过几点可确定一条直线?(3)过几个点可以确定一个圆呢?过一点有无数条直线.过两点可确定一条直线.通过对已经学过的知识的回顾,在原有的认知结构基础之上,建立探究新知的桥梁.实践探索一:确定圆的条件1.经过已知点A作圆,可以作多少个?1.学生先思考,然后动手画图,最后总结.总结:经过已知点A作圆,这样的圆有引导学生自主探究,渗透分类的数学思想方法.(师:请你动手画出猜想)无数多个.让学生明白确定一个圆,需要知道圆心和半径,已知圆上的一个点,就是需要确定圆心的位置.2.经过已知点A、B作圆,可以作多少个?圆心在什么图形上?(师:请你动手画出的猜想,你有什么发现?)2.学生先思考,然后动手画图,最后讨论总结.总结:过两点能作无数多个圆.圆心在两点连线的垂直平分线上.一定要让学生发现并得到“到两个点距离相等的点在这条线段的中垂线上”.AAAB3.经过A、B、C三点,能不能作圆?如果能,可以作多少个?圆心在什么位置?如果不能,请说明理由.(教师进行分步引导:A、B、C三点有怎样的位置关系?①如果过三个点,圆心与这三个点有什么关系?②经过A、B的圆心有什么特征?经过B、C的圆心有什么特征?③请你动手画画,你有什么发现?)4.定理:不在同一直线上的三点确定一个圆.3.学生先思考,然后动手画图,最后讨论交流.过三点:若三点不共线,则能唯一确定一个圆.若三点共线,则不能作圆.因为DE∥FG,所以没有交点,即没有过这三点的圆心.要让学生先思考,教师不要一开始提醒学生进行分类,要让学生明白“为什么三点不共线”.让学生自己归纳.ABC●A●B●O●cCGFFDABECF实践探索二:相关概念由定理可知:经过三角形三个顶点可以作一个圆,经过三角形各顶点的圆叫做三角形的外接圆.外接圆的圆心叫做三角形的外心,这个三角形叫做这个圆的内接三角形.1.让学生说说对“外”的理解.2.如图,点A,B,C都在⊙O上,△ABC是⊙O的_________三角形;⊙O是△ABC的_________圆.结合图形,让学生理解外接圆等概念.实践探索三:三角形的外接圆1.已知△ABC,用直尺和圆规作三角形ABC的外接圆.2.想一想:(1)三角形有多少个外接圆?(2)三角形的外心如何确定?它到三角形三个顶点的距离有何关系?(3)圆有几个内接三角形?3.三角形的外接圆有什么性质?1.学生先自己作图,然后交流展示.作法:(1)作线段AB的垂直平分线MN;(2)作线段AC的垂直平分线EF,交MN于点O;(3)连接OB.(4)以O为圆心,OB为半径作圆.⊙O就是所求作的圆.巩固“不在同一直线上的三点确定一个圆”,同时也是定理的直接应用,三角形的外接圆有的性质是定理的总结升华.OABC·ABCO2.学生先独立思考,然后小组讨论,最后交流总结.3.判断题:(1)经过三点一定可以作圆;()(2)任意一个三角形一定有一个外接圆,并且只有一个外接圆;()(3)任意一个圆一定有一个内接三角形,并且只有一个内接三角形;()(4)三角形的外心是三角形三边中线的交点;()(5)三角形的外心到三角形各项点距离相等.()知识应用如何解决“圆形瓷器碎片重圆”的问...