湖南省益阳市六中八年级数学《不等式》教学设计VIP免费

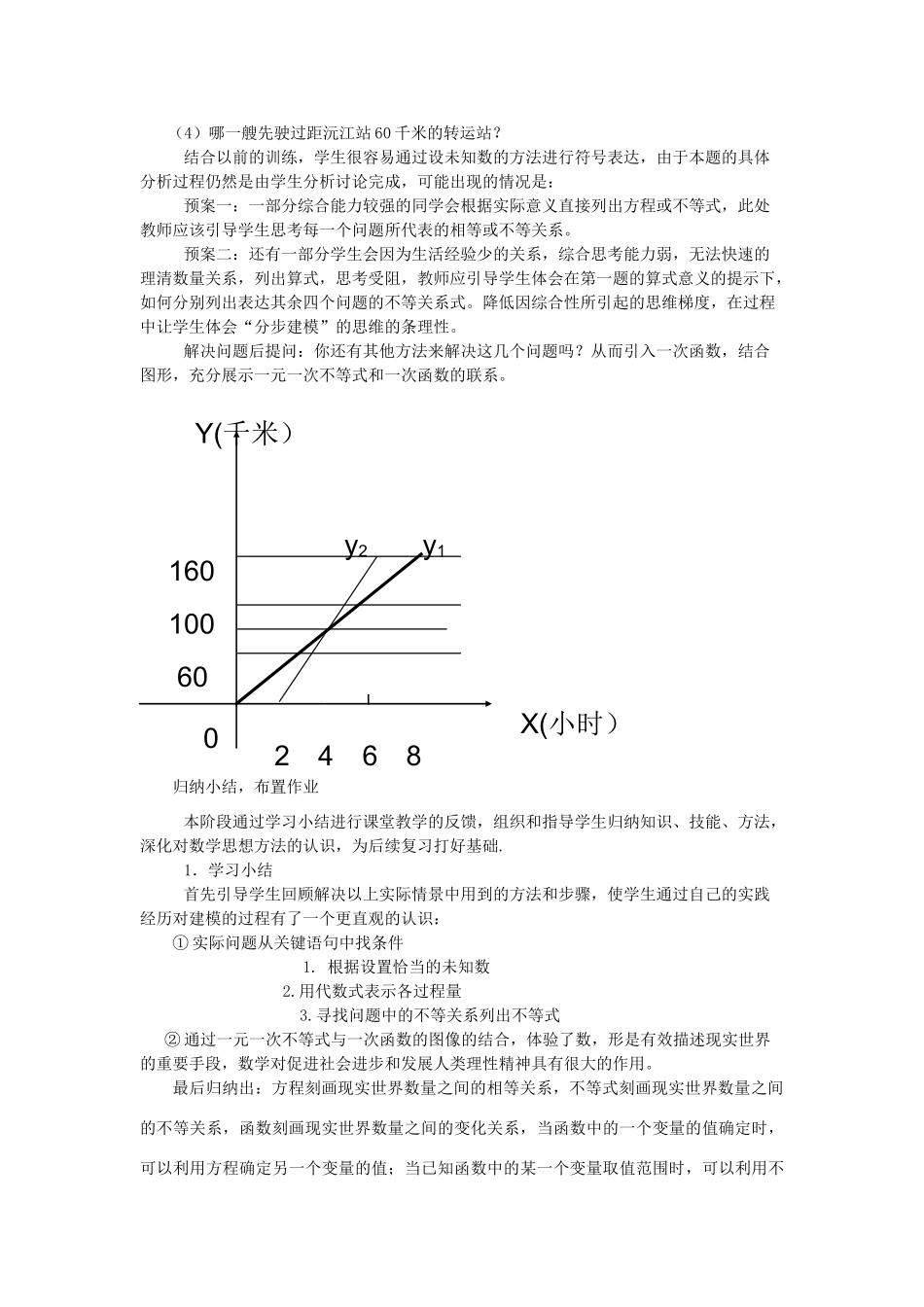
湖南省益阳市六中八年级数学《不等式》教学设计【教材分析】：1.教材的地位和作用（1）本节内容，是在复习了一元一次不等式的性质及其解法等知识的基础上，把实际问题和一元一次不等式结合在一起，既是对已学知识的运用和深化，又是用不等式组解决实际问题以及更广泛的应用数学建模的思想方法的基础，具有在代数学中承上启下的作用；（2）通过本节的学习，学生将继续经历把生活中的数和数量关系转化为数学符号的体验过程，体会不等式和方程，函数一样都是刻画现实世界数量关系的重要模型。（3）在列不等式解决实际问题的探索过程中，渗透建立数学模型，分类讨论等数学思想，对提升学生应用数学意识思考和解决问题的能力起到积极的作用。2.教学的重点和难点对于用不等式解决实际问题，学生容易出现的认知困难主要有两个方面：①哪类的实际问题需要用一元一次不等式来解决；②如何将实际问题转化为一元一次不等式并加以解决。根据以上的分析和《新数学课程标准》对本节内容的教学要求，本节课的教学重点是：一元一次不等式在与一次函数结合的实际问题中的应用；难点是：如何将实际问题中的数量关系图形化，并根据图像结合实际情况分类讨论得出合理结论。【教学目标】：1、知识目标：①能进一步熟练从实际问题中抽象出数学模型，会用一元一次不等式解决简单的实际问题.②领悟不等式中的化归思想，使学生进一步掌握一元一次不等式和一次函数的关系，利用数形结合解决实际问题。2、能力目标：通过观察、实践、讨论等活动，积累利用一元一次不等式解决实际问题的经验，提高分类考虑、讨论问题的能力，理解等与不等的辩证关系，更好地认识和掌握事物运动和变化的规律．感知方程，不等式和一次函数的内在联系，体会这三者同样都是刻画现实世界数量关系的重要模型。3.情感目标：①在积极参与数学学习活动的过程中，形成实事求是的态度和独立思考的习惯。②培养学生合作交流意识，分类思想和探究精神。③体会数学在实际生活中的作用，激发学生爱数学的热情。关键：突出建模思想，刻画出数量关系，从实际中抽象出数量关系。注意问题中隐含的不等量关系，列代数式得到不等式，转化为纯数学问题求解。【教学方法】：1、教学方法根据教学内容、教学目标和学生的认知水平，我主要采取教师启发引导，学生自主探究的教学方法.教学过程中，创设适当的教学情境，引导学生独立思考、共同探究，使学生经历将生活中的数和数量关系转化为数学符号与数学图形的具体建模过程，体会不等式作为刻画现实世界数量关系的重要模型的价值。2、教学手段教学中使用多媒体投影、计算机辅助教学，目的是充分发挥其快捷、生动、形象的特点，为学生提供直观感性的材料，有助于学生对问题的关注和理解，激发学生的学习兴趣.【教学过程】：为了达到本节课的教学目标，突出重点，突破难点，我把教学过程通过一个探究题逐步深入到一个实际问题；最后归纳小结，布置作业.具体过程如下：课题引入:我们已经复习过了一元一次不等式的解法，并在解决许多实际问题的过程中感受到：将数量关系用数学符号抽象后所得到的“方程”和“不等式”确实是一种有效数学工具，它能让我们的思维过程更加准确和简明！今天，就让我们通过一些具有代表性的实际问题来共同探讨一下一元一次不等式这种数学模型是如何解决生活中的实际问题的。实际情景：探究引例：（1）解不等式20x＞40(x-2)。（2）当x为何值时，函数y1=20x的值大于y2=40(x-2)的值？设计意图：引例作为引子，让学生自然地从函数、不等式的知识点切入本节课的教学，学生通过问题的初步探究感知一次函数与一次函数与一元一次不等式的关系，让学生潜意识中生成“一次函数与一元一次不等式”可以从“数”“形”两个方面着手解决的感性认识。预案一：教师应关注学生能否在讨论中认清解不等式和函数中自变量的取值的关系，应关注每一位同学的感受，让同学们充分理解交流，扩大参与思考的广度，获得基本抽象思维的生长点。预案二：有的学生没有注意到两者的关系，只顾做题，教师应从两者的联系加以提示，从而引入本节重点。例1一艘轮船以20千米／小时的速度从沅江站驶向160千米以外的桃江...