SPC理论指导VIP免费

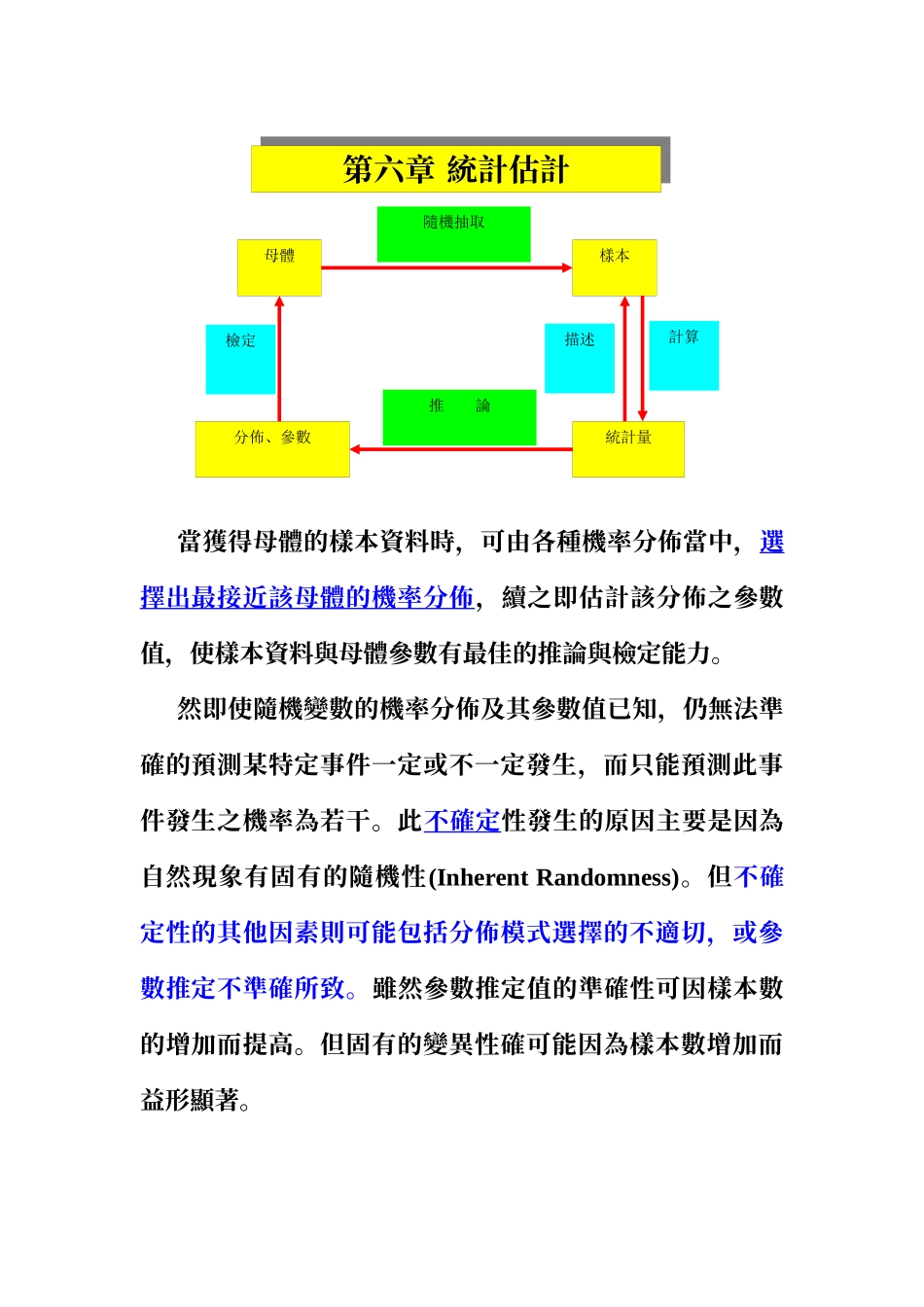
授課目錄第1章導論第2章統計資料的整理與描述第3章機率導論第4章常用的機率分佈與統計分佈第5章描樣方法與描樣分佈第6章統計估計第7章統計檢定第8章變異數分析第9章相關分析與迴歸模式第10章無母數統計檢定第11章類別資料分析---列聯表與卡方檢定母體樣本分佈、參數統計量隨機抽取推論檢定計算描述當獲得母體的樣本資料時，可由各種機率分佈當中，選擇出最接近該母體的機率分佈，續之即估計該分佈之參數值，使樣本資料與母體參數有最佳的推論與檢定能力。然即使隨機變數的機率分佈及其參數值已知，仍無法準確的預測某特定事件一定或不一定發生，而只能預測此事件發生之機率為若干。此不確定性發生的原因主要是因為自然現象有固有的隨機性(InherentRandomness)。但不確定性的其他因素則可能包括分佈模式選擇的不適切，或參數推定不準確所致。雖然參數推定值的準確性可因樣本數的增加而提高。但固有的變異性確可能因為樣本數增加而益形顯著。第六章統計估計母體f(x|)觀測值為x1,x2,…,xnˆ參數的估計值統計估計過程是由母體中抽取出數樣本，藉機率原理找出適當的樣本統計量，再以此樣本統計量推估母體參數。統計估計方法，一般分為點估計與區間估計兩種。6.1點估計(PointEstimation)◎假設隨機變數X的母體機率密度函數f(x|)，其中為未知的參數。為估計此未知的參數，則由母體中抽取出數樣本，得到觀測值為x1,x2,…,xn。◎利用點估計方法求出一估計式(Estimator)，以^θ表示。再將觀測值為x1,x2,…,xn代入估計式中得到一數值，此數值稱之為參數的估計值(Estimate)。◎常用方法：(1)最大概似法，(2)動差法。6.2.1最大概似法(MaximumLikelihoodMethod)◎由Fisher(1912)提出。假設隨機變數X的母體機率密度函數f(x|)，其中為未知的參數，為估計此未知的參數，則由母體中抽取出數樣本，得到觀測值為x1,x2,…,xn。則概似函數定義為L(x1,x2,…,xn；)=f(x1,)f(x2,)…f(xn,)(6.1)◎使概似函數L(x1,x2,…,xn；)值為最大，則能求出估計式^θ，稱此^θ為最大概似估計式(MLE,MaximumLikelihoodMethod)母體f(x)=(1/)e-x/觀測值為8，10，13，14，19，21，27，28，34，41，52ˆˆ範例、某公司新推出光碟燒錄機，其使用壽命服從指數分佈f(x)=(1/)e-x/。為估計參數以了解平均使用壽命，隨機抽取出11台樣本做測試，測得其壽命結果如下：8，10，13，14，19，21，27，28，34，41，52(百小時)。試以最大概似法估計值。SOL：L(x1,x2,…,xn；)=f(x1,)f(x2,)…f(xn,)=1θe−x1/θ⋅1θe−x2/θ¿⋯1θe−xn/θ=(1θ)ne−∑i=1nxi/θlnL(x1,x2,…,xn；)=-nln-(1/)ni=1xid(lnL)/d=-n/+(1/2)ni=1xi=0Estimator(估計式)^θ=ni=1xi/n^θ=(8+10+13+14+19+21+27+28+34+41+52)/11=267/11範例、假設隨機變數X~N(,2)，從其中隨機抽取出一組樣本x1,x2,…,xn，試以最大概似法估計,2值。SOL：L(x1,x2,…,xn；,2)=f(x1,,2)f(x2,,2)…f(xn,,2)=1√2πσe−(x1−μ)22σ2⋯1√2πσe−(xn−μ)22σ2=(1√2πσ)ne−∑(xi−μ)22σ2lnL(x1,x2,…,xn；,2)=ln(1√2πσ)ne−∑(xi−μ)22σ2=-(n/2)ln(2)-(n/2)ln(2)-((xi-)2)/22∂lnL(μ,σ2)∂μ=0⇒^μ=1n∑i=1nxi=¯x∂lnL(μ,σ2)∂σ2=0⇒^σ2=1n∑i=1n(xi−¯x)2範例、台灣的地理位置處於東亞地震帶，地震活動較頻繁假設台灣發生有感地震的次數服從卜氏分佈Poi()。台東氣象站為了要估計此參數，以了解台灣有感地：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：：9,7,12,14,3,11,7,10,4,6,8,10。試以最大概似法求之估計式，並由樣資料去估計值。SOL：L(x1,x2,…,xn；)=f(x1,)f(x2,)…f(xn,)=e−μμx1x1!⋅e−μμx2x2!¿⋯e−μμxnxn!=e−nμμ∑i=1nxiΠi=1nxi!lnL(x1,x2,…,xn；)=-n+ni=1xiln-lnni=1xi!d(lnL)/d=-n+(ni=1xi)/=0Estimator(估計式)^μ=ni=1xi/n^μ=(9+7+12+14+3+11+7+10+4+6+8+10)/12=101/12=8.426.2.2動差法(MomentMethod)◎由Pearson(1894)提出。假設隨機變數X的k次動差為k=E[Xk]，則樣本動差...