初中手拉手全等模型精编版VIP免费

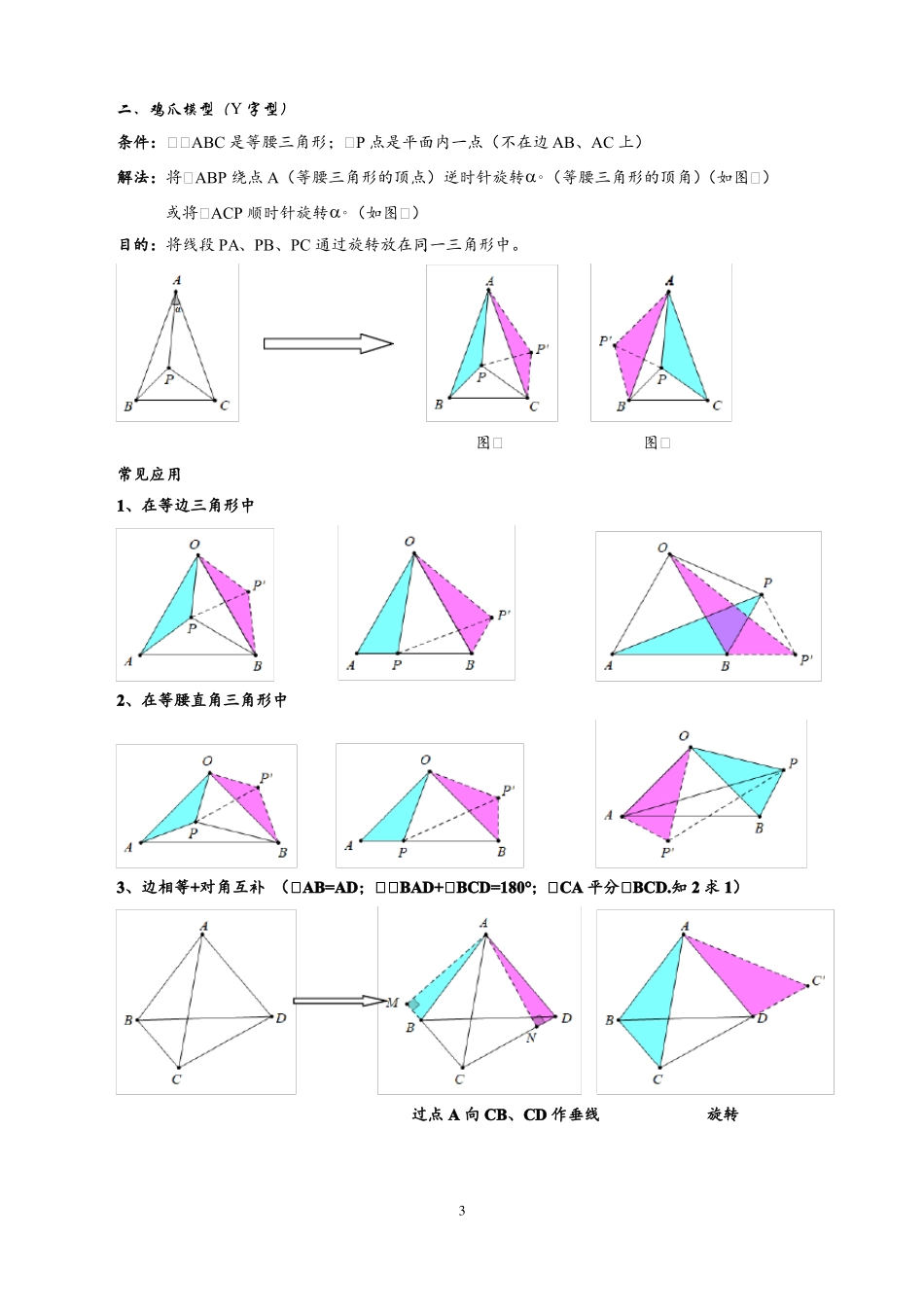
勾股定理与图形旋转手拉手模型（一点四线）条件：①两等腰三角形（OA=OB，OC=OD）；①等腰三角形共顶点。结论：①①OAC①①OBD；①对应边夹角等于旋转角（如图3）；①旋转中心与第三边对应点交点的连线平分第三边夹角的邻补角（ON平分①PNQ，如图4）图①图①图①图①常见应用图①图①图①共顶点的等边三角形共顶点的等腰直角三角形共顶点的正方形常见构造一、半角模型条件：①OA=OB；①①EOF=1①AOB2解法：将①OAE逆时针旋转（如图①）；或者将①OBF顺时针旋转（如图①）。目的：将线段AE、EF、BF通过旋转放在同一三角形中。图①图①1常见应用1、等腰直角三角形中90°夹45°（如图①、①）；含90°的四边形中夹45°（如图①）结论：EF2=AE2+BF2（图①、图①）；图①中的结论：I、EF=AE+CF；II、C①BEF=AB+BC；III、OE平分①AEF，OF平分①CFE图①图①图①特别的：含135°的三角形中夹等腰直角三角形结论：EF2=BE2+AF22、正方形中夹45°结论：（1）EF2BE2DF2；（2）MNBMDN；（3）△CMN的周长等于正方形边长的2倍；（4）AM平分①BMN，AN平分①DNM；（5）点A到MN的距离等于正方形的边长（即AP=AB）；（6）S正方形ABCD:SAMN2AB:MN；（7）S△AMN2S△AEF；（△AMN相似于△AFE）（8）△AEN、△AFM都为等腰直角三角形（过点F向AB、BC边作垂线）；3、含120°的等腰三角形中夹60°（解含有特殊角的三角形）2二、鸡爪模型（Y字型）条件：①①ABC是等腰三角形；①P点是平面内一点（不在边AB、AC上）解法：将①ABP绕点A（等腰三角形的顶点）逆时针旋转（等腰三角形的顶角）（如图①）或将①ACP顺时针旋转（如图①）目的：将线段PA、PB、PC通过旋转放在同一三角形中。常见应用1、在等边三角形中图①图①2、在等腰直角三角形中3、边相等+对角互补（①AB=AD；①①BAD+①BCD=180°；①CA平分①BCD.知2求1）过点A向CB、CD作垂线旋转34、边相等+特殊角本图中结论：BD2=CD2+2AD2三、费马点问题（最值问题）条件：若点P是△ABC内任意一点，试找PA+PB+PC的最小值．解法：将△APC绕点A逆时针旋转60°（费马点问题只能旋转60°）．目的：将线段PA、PB、PC通过旋转放在同一方向上．结论：PA+PB+PC=PPPBPCBC费马点性质：1、费马点到三角形三个顶点的距离之和最小；2、费马点连接三个顶点所成的三夹角均为120°．确定方法：1、如果三角形有一个内角大于或等于120°，这个内角的顶点就是费马点；2、如果3个内角均小于120°，则在三角形内部对3边张角均为120°的点就是费马点．费马点最小值快速求解：以三角形任意一边为边向外作等边三角形，这条边所对两顶点的距离即为最小值．4例1：如图所示，在等腰直角ABC的斜边AB上取两点M、N，使MCN45，记AMm，MNx，BNn，求证：以x、m、n为边长的三角形的形状是直角三角形.CAmMxNnB练习：已知：如图1在RtABC中，BAC90，ABAC，点D、E分别为线段BC上两动点，若DAE45．探究线段BD、DE、EC三条线段之间的数量关系．（1）当动点E在线段BC上，动点D运动在线段CB延长线上时，如图1，写出线段BD、DE、EC三条线段之间的数量关系并给予证明．（2）若AB=2，求DE的最小值．5例2：如图，P是等边ABC内一点，若AP3，PB4，PC5，求APB的度数．练习：1、如图所示，P是等边ABC中的一点，PA2，PB23，PC4，试求ABC的边长.62、如图，P是等边ABC外的一点，PA3，PB4，PC5，求APB的度数．3、如图所示：ABC中，ACB90，ACBC，P是ABC内的一点，且AP3，CP2，BP1，求BPC的度数．74、P为等边ABC内一点，APB113，APC123，求证：以AP、BP、CP为边可以构成一个三角形，并确定所构成的三角形的各内角的度数.PD2，PC3，5、如图，P为正方形ABCD内一点，PA1，将PDC绕着D点按逆时针旋转90到PQD的位置。（1）求PQ:PD的值；（2）求APD的度数。86、在凸四边形ABCD中，ABC30，ADC60，ADCD，求证：BD2AB2BC2．例3：如图所示，ABD是等边三角形，在ABC中，BCa，CAb，问：当ACB为何值时，C、D两点的距离最大？最大值是多少？练习：如...