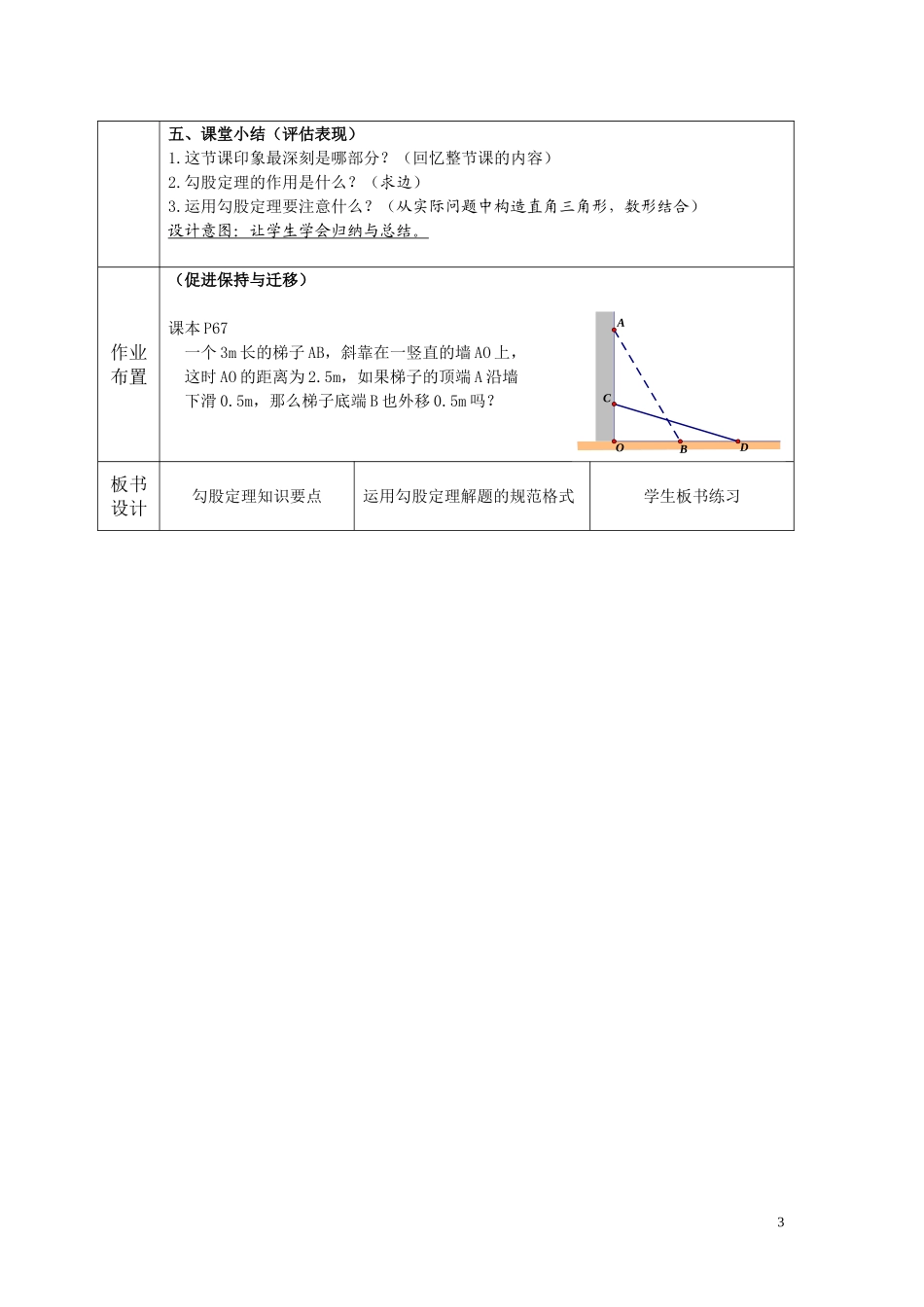
科学课堂说课比赛教学设计学科数学年级初二备课主笔刘爱心课题17.1勾股定理课型新授课教学目标1.能从几何证明方向探索出勾股定理并用数学语言描述;2.能简单运用勾股定理求直角三角形的边长;3.能从实际问题中构造直角三角形,并运用勾股定理解决问题。教学重点、难点重点:勾股定理的探索及简单运用。难点:边与边之间的数量关系的探索,从实际问题中构造直角三角形。教学过程设计一、创设情境(引起注意、告之目标)有一天晚上,你爸爸妈妈在争论一个问题:这块木板能否进12楼那位客户的门呢?妈妈说:“横竖都进不去。”爸爸说:“斜着能进去不?”你很想帮助爸爸妈妈,免得进不了门白跑一趟。于是你在QQ里图1向老师请求帮助。老师回复了你一张《赵爽弦图》。你看到图后不明白老师到底想表达什么意思(图1)。老师又发了密钥:这图里有四个全等的直角三角形和两个正方形,并列出了3个问题,然后道晚安。让我们一起来解密吧。设计意图:设计情境吸引学生。二、自主探索(刺激回忆先前学习的知识、呈现新的学习内容)1.探索大小正方形与直角三角形面积之间的等量关系S大正=S小正+4S直角三角形2.探索大小正方形的边长与直角三角形的边长有何关系(1)直角三角形的斜边=大正方形的边长(2)直角三角形大直角边与小直角边的差=小正方形的边长3.探索如何用最少字母表示图中线段如图2图2设计意图:铺设问题作为探索勾股定理的阶梯,降低难度。4.得出结论:你知道了什么?S大正=S小正+4S直角三角形=(b-a)2+4×1/2ab1bac21BDCABC32.2化简得:=+(1)原来老师想告诉我们勾股定理:如图3,如果直角三角形的两直角边长分别为a,b,斜边长为c,那么=+数学语言描述:在Rt△ABC中,∠C=90°,则=+图3(2)老师还告诉我们勾股定理的作用:在直角三角形中,知两边可求第三边。=+,任意知两边便可以构建一元二次方程求出第三边。34810513设计意图:探索勾股定理的简单运用。三、运用新知(提供学习指导)解密成功太高兴了,于是你运用勾股定理帮助父母解决了“木板能否通过门”的问题。解:如图6,在Rt△ABC中,∠B=90°,根据勾股定理AB2+BC2=AC2所以,12+22=AC2AC=±因为在实际问题中,长度是非负数,因此:AC=≈2.24因为2.24>2.2所以木板能通过门框。设计意图:以实际问题为例,学会把实际问题转化为直角三角形三边关系的问题,并运用勾股定理解决。图6四、巩固新知(引发行为反应,提供反馈)基础练习:课本P68,1有一个边长为50cm的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)设计意图:把实际问题转化为直角三角形三边关系问题,培养学生数形结合的思想。2cbaBCA21BDCABC32.221ABCOBCABCA五、课堂小结(评估表现)1.这节课印象最深刻是哪部分?(回忆整节课的内容)2.勾股定理的作用是什么?(求边)3.运用勾股定理要注意什么?(从实际问题中构造直角三角形,数形结合)设计意图:让学生学会归纳与总结。作业布置(促进保持与迁移)课本P67一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?板书设计勾股定理知识要点运用勾股定理解题的规范格式学生板书练习3BACDO