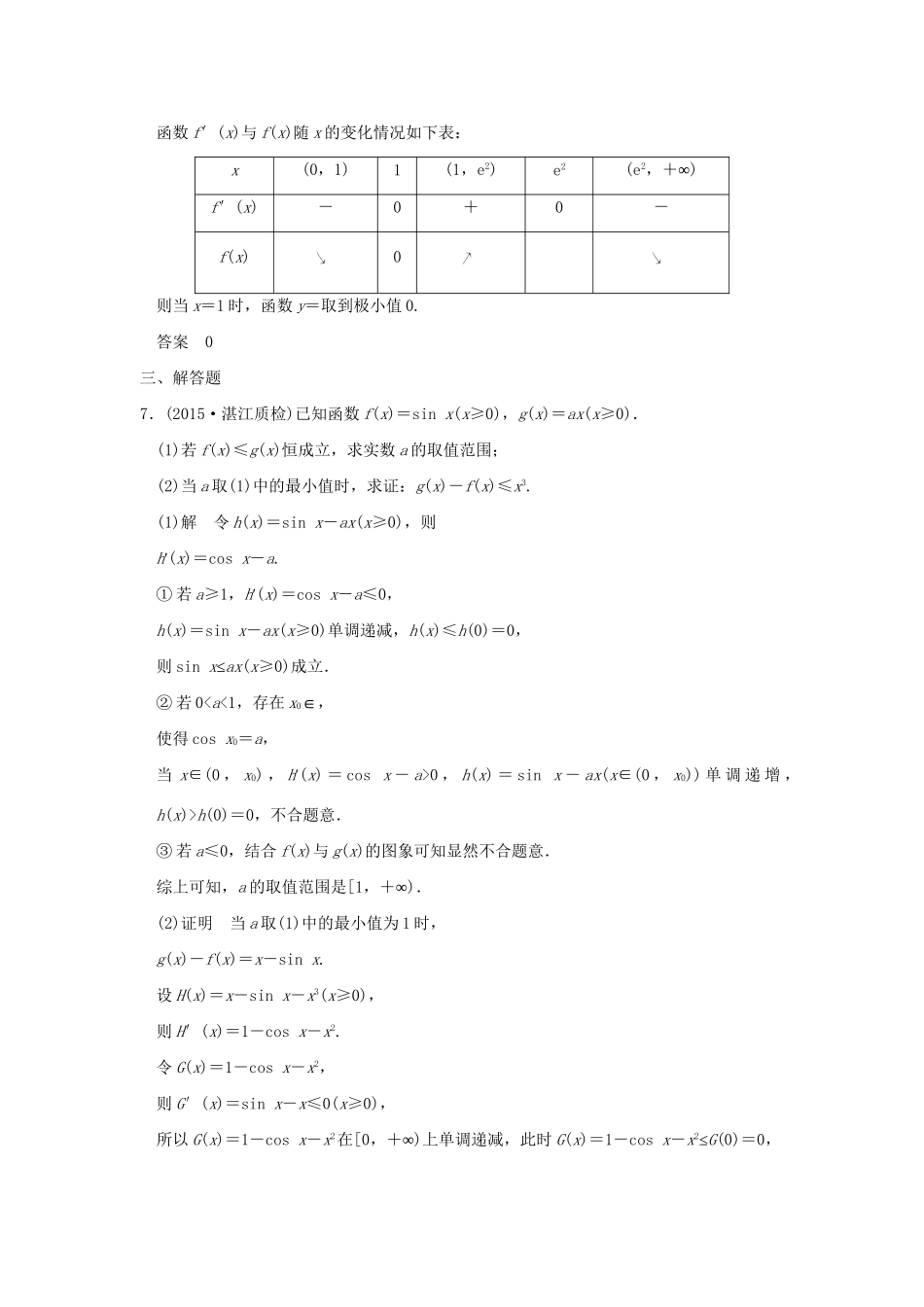
A组专项基础测试三年模拟精选一、选择题1.(2015·江西新余模拟)如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是()A.B.(1,2)C.D.(2,3)解析函数f(x)=x2+ax+b的部分图象得0<b<1,f(1)=0,从而-2<a<-1,而g(x)=lnx+f′(x)在定义域内单调递增,g=ln+1+a<0,g(1)=ln1+2+a=2+a>0,∴函数g(x)=lnx+f′(x)的零点所在的区间是,故选C.答案C2.(2015·河北恒台模拟)设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x)…,,fn(x)=fn-1′(x),n∈N,则f2015(x)=()A.sinxB.-sinxC.cosxD.-cosx解析f0(x)=sinx,f1(x)=f0′(x)=cosx,f2(x)=f1′(x)=-sinx,f3(x)=f2′(x)=-cosx,f4(x)=f3′(x)=sinx,…由上面可以看出,以4为周期进行循环.所以f2015(x)=f3(x)=-cosx,故选D.答案D3.(2015·江西新余模拟)设点P在曲线y=ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为()A.1-ln2B.(1-ln2)C.1+ln2D.(1+ln2)解析函数y=ex和函数y=ln(2x)互为反函数图象关于y=x对称.则只有直线PQ与直线y=x垂直时|PQ|才能取得最小值.设P,则点P到直线y=x的距离为d=,令g(x)=ex-x,(x>0),则g′(x)=ex-1,令g′(x)=ex-1>0得x>ln2;令g′(x)=ex-1<0得0
0,所以dmin=.则|PQ|=2dmin=(1-ln2).故B正确.答案B4.(2013·浙江温州模拟)已知定义域为R的函数f(x)满足:f(4)=-3,且对任意x∈R总有f′(x)<3,则不等式f(x)<3x-15的解集为()A.(∞-,4)B.(∞-,-4)C.(∞-,-4)∪(4,∞+)D.(4,∞+)解析记g(x)=f(x)-3x+15,则g′(x)=f′(x)-3<0,可知g(x)在R上为减函数.又g(4)=f(4)-3×4+15=0,所以f(x)<3x-15可化为f(x)-3x+15<0,即g(x)4.答案D5.(2013·北京朝阳调研)已知函数f(x)=x4-2x3+3m,x∈R,若f(x)+9≥0恒成立,则实数m的取值范围是()A.B.C.D.解析因为函数f(x)=x4-2x3+3m,所以f′(x)=2x3-6x2,令f′(x)=0,得x=0或x=3,经检验知x=3是函数的一个极小值点,所以函数的最小值为f(3)=3m-,不等式f(x)+9≥0恒成立,即f(x)≥-9恒成立,只需3m-≥-9,解得m≥.答案A二、填空题6.(2014·山西临汾一模)函数y=的极小值为______.解析函数的定义域为(0,∞+),令y=f(x),f′(x)==.令f′(x)=0,解得x=1或x=e2.函数f′(x)与f(x)随x的变化情况如下表:x(0,1)1(1,e2)e2(e2,∞+)f′(x)-0+0-f(x)0则当x=1时,函数y=取到极小值0.答案0三、解答题7.(2015·湛江质检)已知函数f(x)=sinx(x≥0),g(x)=ax(x≥0).(1)若f(x)≤g(x)恒成立,求实数a的取值范围;(2)当a取(1)中的最小值时,求证:g(x)-f(x)≤x3.(1)解令h(x)=sinx-ax(x≥0),则h′(x)=cosx-a.①若a≥1,h′(x)=cosx-a≤0,h(x)=sinx-ax(x≥0)单调递减,h(x)≤h(0)=0,则sinx≤ax(x≥0)成立.②若00,h(x)=sinx-ax(x∈(0,x0))单调递增,h(x)>h(0)=0,不合题意.③若a≤0,结合f(x)与g(x)的图象可知显然不合题意.综上可知,a的取值范围是[1,∞+).(2)证明当a取(1)中的最小值为1时,g(x)-f(x)=x-sinx.设H(x)=x-sinx-x3(x≥0),则H′(x)=1-cosx-x2.令G(x)=1-cosx-x2,则G′(x)=sinx-x≤0(x≥0),所以G(x)=1-cosx-x2在[0,∞+)上单调递减,此时G(x)=1-cosx-x2≤G(0)=0,即H′(x)=1-cosx-x2≤0,所以H(x)=x-sinx-x3在x∈[0,∞+)上单调递减.所以H(x)=x-sinx-x3≤H(0)=0,则x-sinx≤x3(x≥0).所以,当a取(1)中的最小值时,g(x)-f(x)≤x3.一年创新演练8.函数y=x+2cosx在区间上的最大值是______.解析y′=1-2sinx,令y′=0,且x∈,得x=,则x∈时,y′>0;x∈时,y′<0,故函数在上递增,在上递减,所以当x=时,函数取最大值为+.答案+B组专项提升测试三年模拟精选一、选择题9.(2015·辽宁沈阳模拟)已知定义域为R的奇函数y=f(x)的导函数...