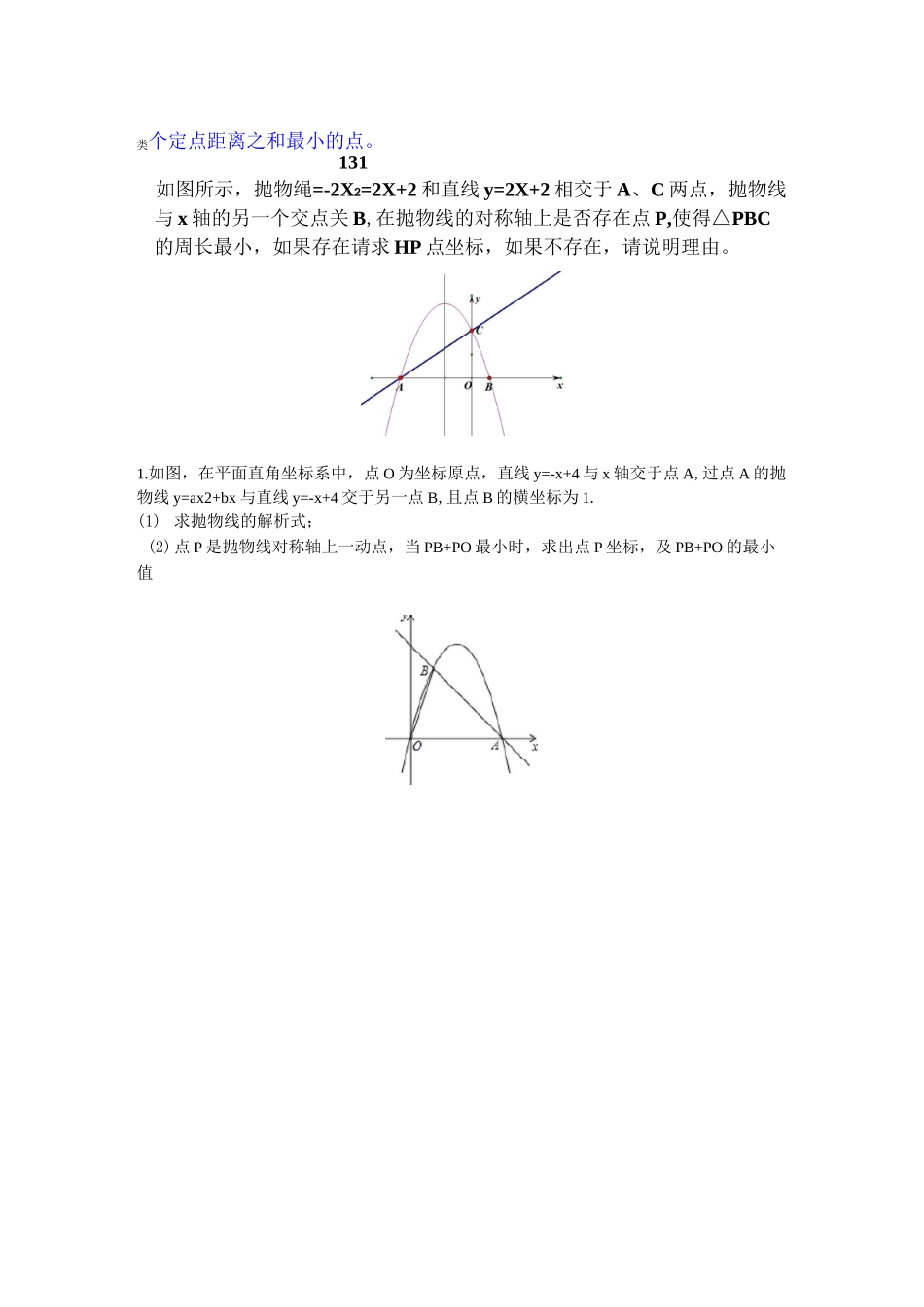
再乘以二分之一来求。131如图所示,抛物线2直产+刑直线右x+2相交于、C两点,抛物线与x轴的另一个交点为在直线C勺上方的抛物线上是否存使怨PAC的面积最大,如果存在请P求坐标,如果不存在,请说明理由。1.如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).(1)求抛物线的解析式(2)过x轴上点E(a,0)(E点在B点的右侧)作直线EF〃BD,交抛物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.(3)在二次函数上有一动点P,过点P作PM丄x轴交线段BD于点M,判断PM有最大值还是有最小值,如有,求出线段PM长度的最大值或最小值.2.如图抛物线与x轴交于A、B两点,与y轴交于C点,且抛物线的解析式为y=-x2+2x+3.(1)求A、B、C的坐标;(2)若动点D在第一象限的抛物线上,求△BDC面积最大时D点的坐标,并求出ABDC的最大面积。类个定点距离之和最小的点。131如图所示,抛物绳=-2X2=2X+2和直线y=2X+2相交于A、C两点,抛物线与x轴的另一个交点关B,在抛物线的对称轴上是否存在点P,使得△PBC的周长最小,如果存在请求HP点坐标,如果不存在,请说明理由。1.如图,在平面直角坐标系中,点O为坐标原点,直线y=-x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=-x+4交于另一点B,且点B的横坐标为1.(1)求抛物线的解析式;(2)点P是抛物线对称轴上一动点,当PB+PO最小时,求出点P坐标,及PB+PO的最小值类分三种情况进行讨论,其中要应用勾股定理等知识。131如图所示,抛物线2卩2%+2和直线=2%+湘交于A、C两点,抛物线与x轴的另一个交点为在抛物线的对称轴上是否存使点△PBC为直角三角形,如果存在请求点坐标,如果不存在,请说明理由。1.如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.(1)求抛物线的解析式;(2)设点D的横坐标为m,△ACD的面积为S求出S与m的函数关系式,并确定m为何值时S有最大值,最大值是多少?(3)若点P是抛物线对称轴上一点,是否存在点P使得ZAPC=90°?若存在,请直接写出点P的坐标;若不存在,请说明理由.如图所示,2线;x+和直线1x+相目交于C两点,抛物线与类其中要应用两点之间的距离公式等知识。域由的另一个交点在抛物线的对称轴上是否得在点为等腰三角形,如果存在点坐标,如果不存在,请说明理由。1.在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(-1,0),B(3,0),与y轴相交于点C.(1)求这条抛物线的解析式;(2)经过点D(2,2)直线与抛物线交于M,N两点,若线段MN正好被直线BC平分,求直线MN的解析式;(3)直线x=a上存在点P,使得△PBC为等腰三角形?若这样的点P有且只有三个,请直接写出符合条件的a值及其取值范围PSQ另此类问题分别以已知的1段3边及对角线1行讨论,其中要应用如图所示,抛物=|妙2只+刑直线=2只+2相交于、C两点,抛物线与x轴的另一物交点为点?在抛物线上2xy在上有一个两Q是否存在点类型五练习’1如图所示,拋物线¥=-|x2-|X4-2和直线y=|x+2相交于爪匚两点,拋物线与H轴的另一个交点为B,H为B匚的中点,点P在拋物线上,在¥轴上有f动点Q,是否存在点P,Q使得以九H,P,Q为顶点的四边形是平行四边形,如果存在请求岀P点坐标,如果不存在,请说明理由。类两边分两种情况对应,同时还有注意到位置的情况。此类问题首先找出一13等的角,即1应角,再把夹这个角的两麵图所示况抛物线+和直线2x+相交于C两点,抛物线与相轴于两点个抛点否存在以点A为果存点为请求出所有点足条件的証。点坐标足条件的类型六练习:如图所示,抛物线習一钗三―(X+2和直线y=-x+2相交于A、C两点,抛物线与)t轴的另一个交点为B,点P是对称轴上一个动点,设对称轴与X轴的交点为Q,是否存在以点P,Q,A为顶点的三角形与三角形ABC相似,如果存在请求出P点坐标,如果不存在,请说明理由■>如果不存在况请说明理由。此类问题要注意到平移抛物小不变,对于般类型七:抛物线的几何变换(平移):只患(值发生改变,对于顶点式只是顶点坐标发生改变。131如图所示,抛y物线和直线=x+相交于.C两点,抛物线与遴由的另一个交点为将抛物...