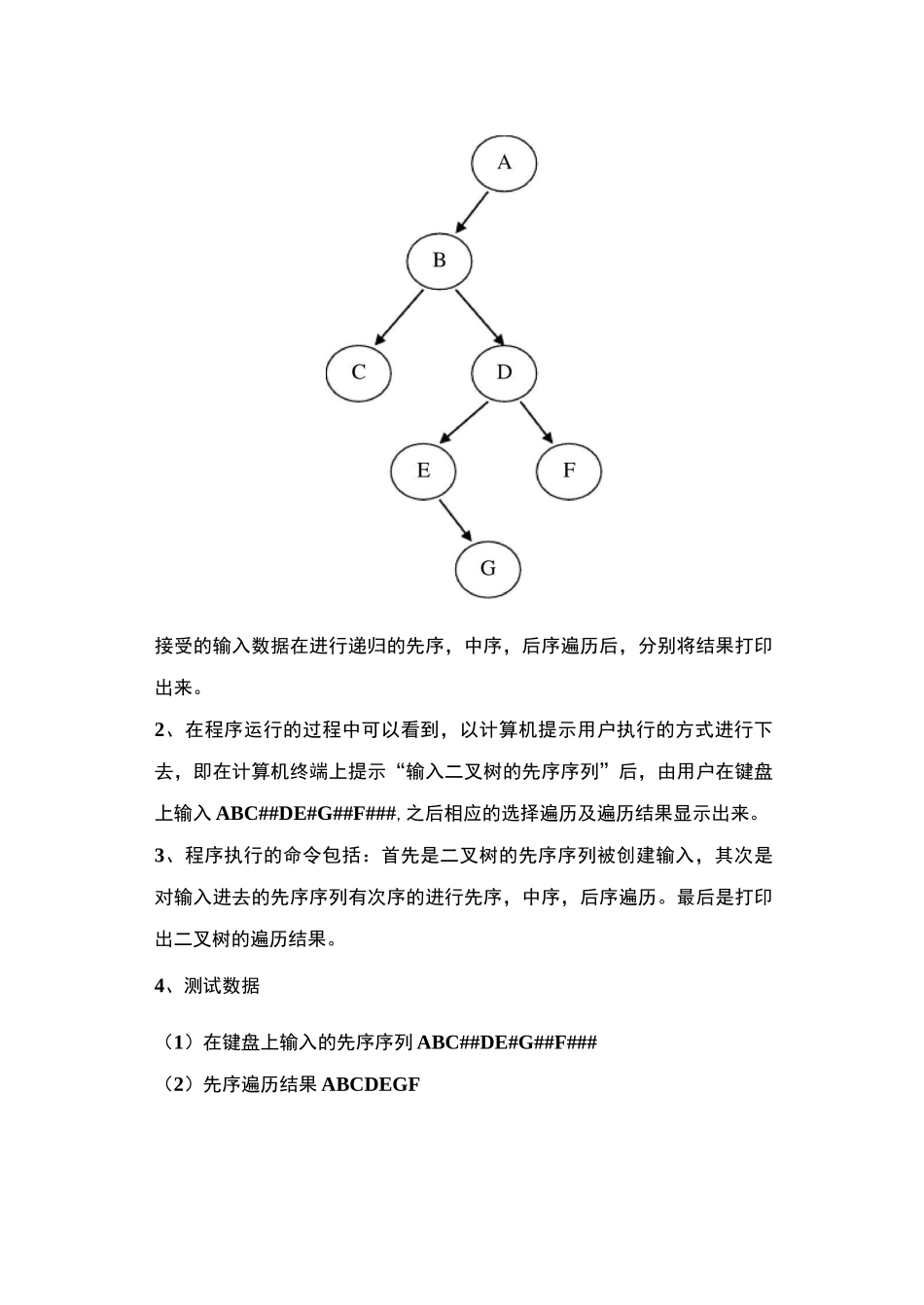
实验目的(1)学会用先序创建一棵二叉树。(2)学会采用递归算法对二叉树进行先序、中序、后序遍历。(3)学会打印输出二叉树的遍历结果。实验内容【问题描述】建立一棵二叉树,并对其进行遍历(先序、中序、后序),打印输出遍历结果。【基本要求】从键盘接受输入(先序),以二叉链表作为存储结构,建立二叉树(以先序来建立),并采用递归算法对其进行遍历(先序、中序、后序),将遍历结果打印输出。【测试数据】ABC中中DE中G中中F中中中(其中中表示空格字符)则输出结果为先序:ABCDEGF中序:CBEGDFA后序:CGBFDBA【选作内容】采用非递归算法实现二叉树遍历。实验步骤(一)需求分析1、在这个过程中,接受遍历的二叉树是从键盘接受输入(先序),以二叉链表作为存储结构,建立的二叉树。因此,首先要创建一棵二叉树,而这棵二叉树是先序二叉树。本演示程序中,集合的元素设定为大写字母ABCDEFG,输出的先序,中序,后序遍历分别为ABCDEGF,CBEGDFA,CGBFDBA。二叉树可以表示为:接受的输入数据在进行递归的先序,中序,后序遍历后,分别将结果打印出来。2、在程序运行的过程中可以看到,以计算机提示用户执行的方式进行下去,即在计算机终端上提示“输入二叉树的先序序列”后,由用户在键盘上输入ABC##DE#G##F###,之后相应的选择遍历及遍历结果显示出来。3、程序执行的命令包括:首先是二叉树的先序序列被创建输入,其次是对输入进去的先序序列有次序的进行先序,中序,后序遍历。最后是打印出二叉树的遍历结果。4、测试数据(1)在键盘上输入的先序序列ABC##DE#G##F###(2)先序遍历结果ABCDEGF//先序遍历//访问结点//先序遍历左子树//先序遍历右子树3)中序遍历结果CBEGDFA4)后序遍历结果CGBFDBA二)概要设计1、为实现上述程序功能,应以二叉树定义的相关操作和二叉树递归遍历的相关操作为依据。有关以二叉链表作为存储结构,建立二叉树的操作为:typedefBTNode*BTree;//定义二叉树的指针BTreeCreatBTree(void){BTreeT;charch;if((ch=getchar())=='#')return(NULL);//读入#,返回空指针else{T=(BTNode*)malloc(sizeof(BTNode));//分配空间,生成结点T->data=ch;T->lchild=CreatBTree();//构造左子树T->rchild=CreatBTree();//构造右子树return(T);}}2、而有关先序、中序、后序遍历的递归操作为:voidPreorder(BTreeT){if(T){printf("%c",T->data);Preorder(T->lchild);Preorder(T->rchild);}}voidInorder(BTreeT)//中序遍历if(T){Inorder(T->lchild);printf("%c",T->data);Inorder(T->rchild);}}//中序遍历左子树//访问结点//中序遍历右字树voidPostorder(BTreeT){if(T){Postorder(T->lchild);Postorder(T->rchild);printf("%c",T->data);}}//后序遍历//后序遍历左子树//后序遍历右子树//访问结点3、本程序包含的模块1)结点单元模块2)构建先序二叉树模块3)二叉树遍历模块4)主程序模块各模块之间的调用关系如下://二叉树的元素类型//自定义二叉树的结类型//定义二叉树的指针//定义输入的数据类型//支持在键盘上输入先序二叉树//读入#,返回空指针三)详细设计1、元素类型,结点类型和指针类型typedefstructnode{chardata;structnode*lchild;structnode*rchild;}BTNode;typedefBTNode*BTree;2、定义类型之后,要以二叉链表作为存储结构,建立二叉树(以先序来建立)。BTreeCreatBTree(void){BTreeT;charch;if((ch=getchar())=='#')return(NULL);对于二叉树的先序输入,在输入中要注意的是对于空指针的把握,由于是先序输入,在输入时要在确定的位置输入“#”号,否则先序二叉树将不完整。else{T=(BTNode*)malloc(sizeof(BTNode));//分配空间,生成结点T->data=ch;T->lchild=CreatBTree();//构造左子树T->rchild=CreatBTree();//构造右子树return(T);}}当输入的叶子结点完整之后,要return(T),否则输入将一直持续二叉树遍历模块//先序遍历//访问结点//先序遍历左子树//先序遍历右子树//中序遍历//中序遍历左子树//访问结点下去不能跳出来。在程序的设计过程中,在适当的位置插入#对于二叉树的遍历有着十分重要的作用,因此要明白二叉树的先序创建过程如何运行。3、对于二叉树...