高三数学导数的应用知道精讲VIP免费

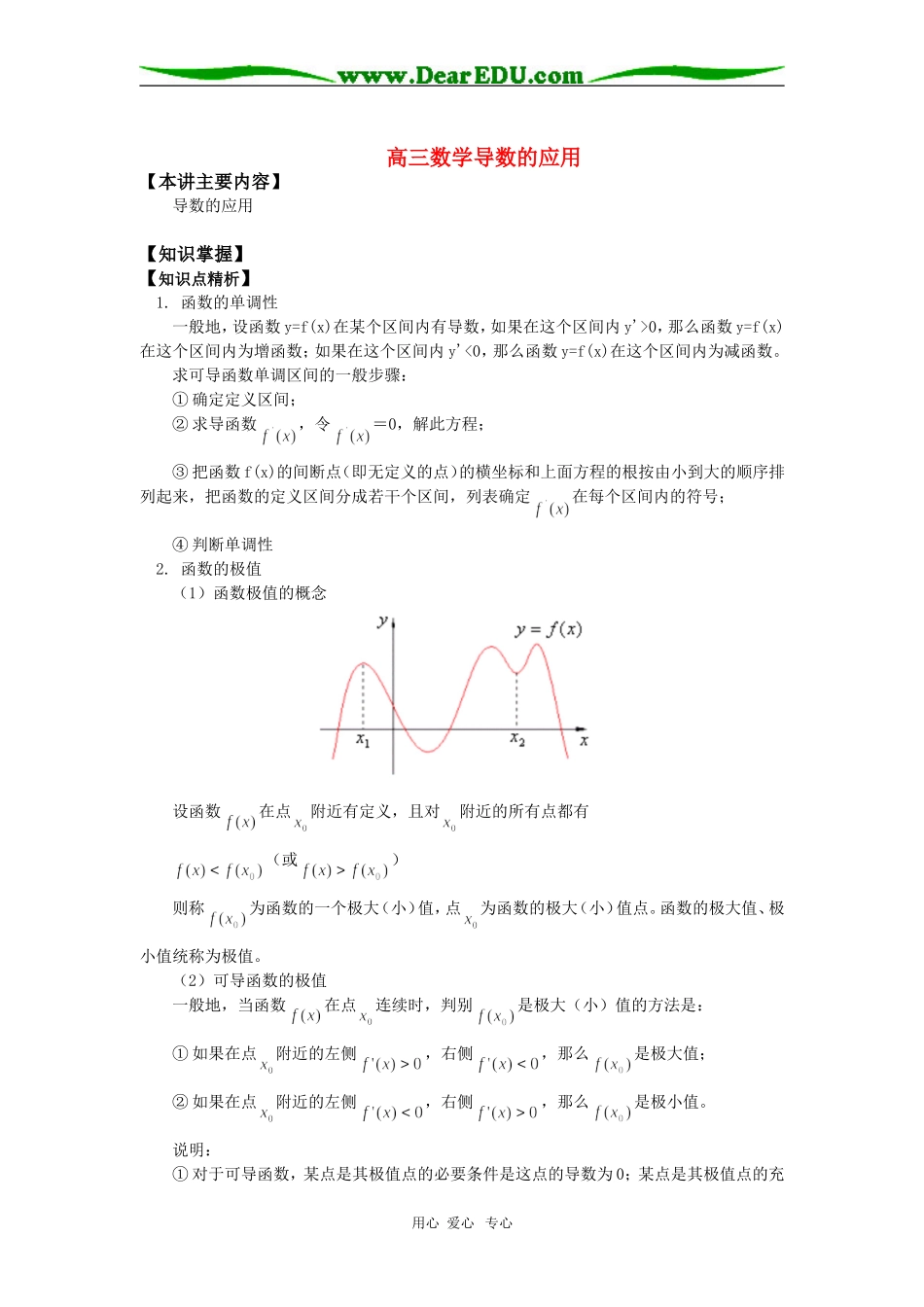
高三数学导数的应用【本讲主要内容】导数的应用【知识掌握】【知识点精析】1.函数的单调性一般地，设函数y=f(x)在某个区间内有导数，如果在这个区间内y'>0，那么函数y=f(x)在这个区间内为增函数；如果在这个区间内y'<0，那么函数y=f(x)在这个区间内为减函数。求可导函数单调区间的一般步骤：①确定定义区间；②求导函数，令＝0，解此方程；③把函数f(x)的间断点（即无定义的点）的横坐标和上面方程的根按由小到大的顺序排列起来，把函数的定义区间分成若干个区间，列表确定在每个区间内的符号；④判断单调性2.函数的极值（1）函数极值的概念设函数在点附近有定义，且对附近的所有点都有（或）则称为函数的一个极大（小）值，点为函数的极大（小）值点。函数的极大值、极小值统称为极值。（2）可导函数的极值一般地，当函数在点连续时，判别是极大（小）值的方法是：①如果在点附近的左侧，右侧，那么是极大值；②如果在点附近的左侧，右侧，那么是极小值。说明：①对于可导函数，某点是其极值点的必要条件是这点的导数为0；某点是其极值点的充用心爱心专心分条件是这点两侧的导数异号；（如函数在处导数为0，但不是函数的极值点。）②函数的不可导点也可能是极值点；（如函数在处不可导，但点是函数的极小值点。）③求可导函数的极值的步骤如下：<1>求导数；<2>解方程；<3>用方程的根顺次将函数的定义域分成若干个小区间，并列成表格，根据在每个小区间内的符号判定函数的极值。3.函数的最值（1）一般地，在闭区间[a，b]上连续的函数f(x)在[a，b]上必有最大值与最小值。说明：①在开区间(a，b)内连续的函数不一定有最大值与最小值。如函数在内连续，但没有最大值与最小值；②函数的最值是比较整个定义域内的函数值得出的；函数的极值是比较极值点附近函数值得出的；③函数在闭区间[a，b]上连续，是在闭区间[a，b]上有最大值与最小值的充分条件而非必要条件。（2）设函数在[a，b]上连续，在(a，b)内可导，则求在[a，b]上的最大值与最小值的步骤如下：①求在(a，b)内的极值；②将的各极值与、比较得出函数在[a，b]上的最值。【解题方法指导】例1.求函数y=的极值。解：的定义域为R，且=可知x=1时，=0；而x=0和x=2时，不存在。由x=0，x=1，x=2三点将定义域分成四个区间，列表：x(-，0)0(0，1)1(1，2)2(2，+))('xf-不存在+0-不存在+fx()↓极小值0↑极大值1↓极小值0↑函数有极小值=0，=0，有极大值=1。说明：函数的导数不存在的点也可能是极值点。例2.设x>－2，n∈N，比较与1+nx的大小用心爱心专心解：设函数f(x)＝－（1+nx）（x>－2）当n=1时，f(x)=0当n≥2时，，令得x=0。x(-2，0)0(0，＋∞))('xf-不存在+)(xf↓极小值0↑所以，f(x)≥f(0)＝0。即≥1+nx【考点突破】【考点指要】导数的应用非常广泛，近年来高考中对导数的考查在深度和广度上进一步挖掘，所占比重逐年增加，大约在12分，被大家所重视。在本节中主要以基本概念和基本公式为考查重点。【典型例题分析】例3.（2006，海淀）若函数在区间（1，4）内为减函数，在区间（6，+∞）上为增函数，试求实数a的取值范围。解：函数的导数令，解得x1或xa1当a11即a2时，函数fx()()在，1上是增函数，不合题意当a11即a2时，函数fx()()在，1上为增函数，在（1，a－1）内为减函数，在()a1，为增函数。依题意应有当所以解得所以a的取值范围是[5，7]例4.（2006，天津）已知求函数的单调区间。解：函数f(x)的导数：（I）当a=0时，若x<0，则<0，若x>0,则>0所以当a=0时，函数f(x)在区间（－∞，0）内为减函数，在区间（0，+∞）内为增函数用心爱心专心（II）当a>0时，由202xax，解得xa2或x0由所以，当a>0时，函数f(x)在区间（－∞，－）内为增函数，在区间（－，0）内为减函数，在区间（0，+∞）内为增函数；（III）当a<0时，由2x+ax2>0，解得0－.所以当a<0时，函数f(x)在区间（－∞，0）内为减函数，在区间（0，－）内为增函数，在区间（－，+∞）内为减函数例5.（2006，宣武）已知函数在处取得极值。（1）讨论和是函数的极大值还是极小值；（1）解：，依题意，，即...