第二章 第六节 指数指数函数VIP免费

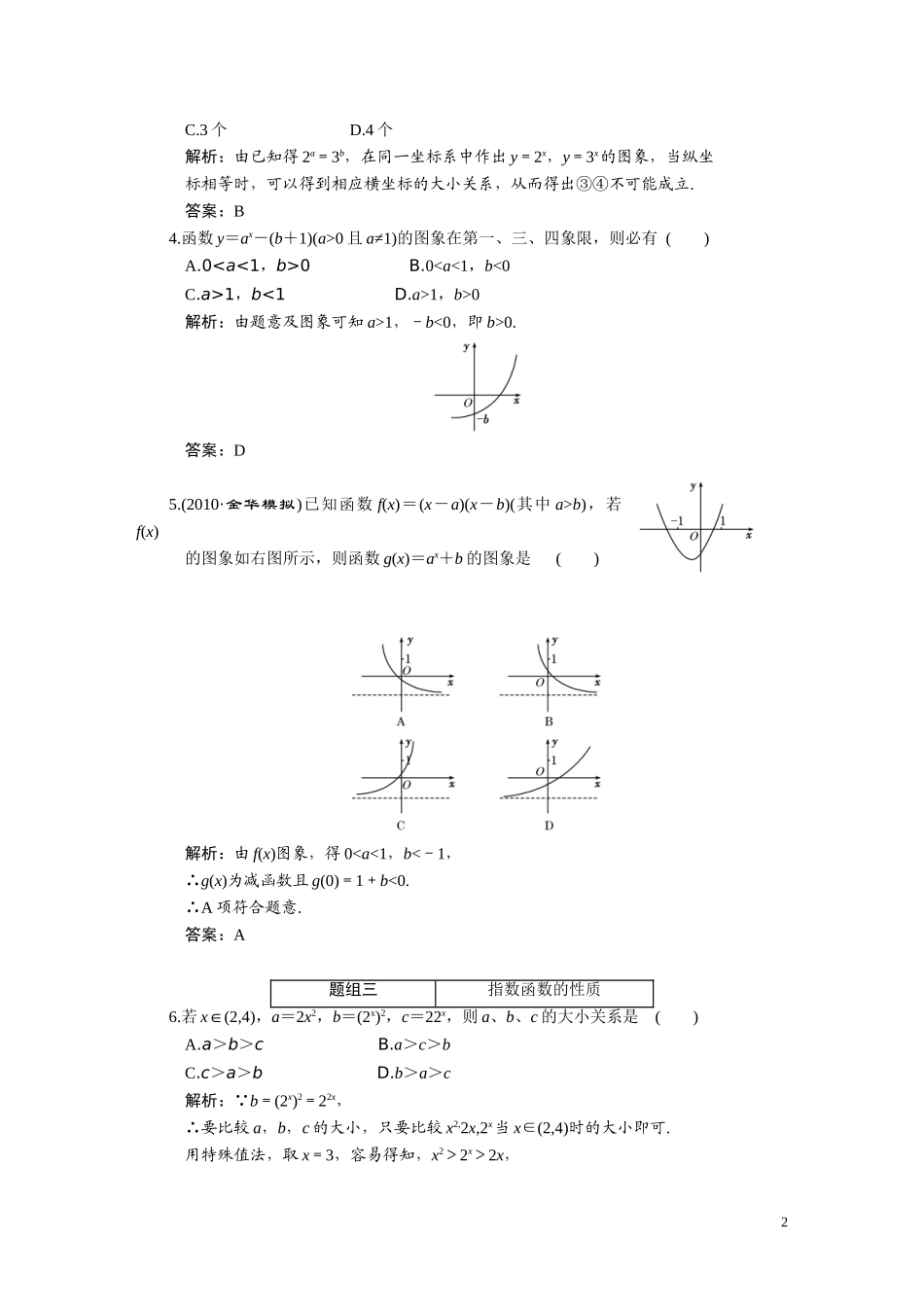
第二章第六节指数、指数函数题组一指数幂的化简与求值1.23338(1)()2772964的值为()A.0B.C.D.解析21(0),(1)(0)xxfxx≤：23338(1)()2772964233332144[()]0.3999()4答案：A2.计算：解：（1）原式=11232227125(1)1100079＝－49＋－1＝－45.(2)原式＝13333322222244100aabb＝a0·b0＝.题组二指数函数的图象及应用3.已知实数a，b满足等式()a＝()b，下列五个关系式：0①＜b＜a；②a＜b＜0；③0＜a＜b；④b＜a＜0；⑤a＝b.其中不可能成立的关系式有()A.1个B.2个1C.3个D.4个解析：由已知得2a＝3b，在同一坐标系中作出y＝2x，y＝3x的图象，当纵坐标相等时，可以得到相应横坐标的大小关系，从而得出③④不可能成立.答案：B4.函数y＝ax－(b＋1)(a>0且a≠1)的图象在第一、三、四象限，则必有()A.00B.01，b<1D.a>1，b>0解析：由题意及图象可知a>1，－b<0，即b>0.答案：D5.(2010·金华模拟)已知函数f(x)＝(x－a)(x－b)(其中a>b)，若f(x)的图象如右图所示，则函数g(x)＝ax＋b的图象是()解析：由f(x)图象，得00，a≠1)，满足f(1)＝，则f(x)的单调递减区间是()A.(－∞，2]B.[2，＋∞)C.[－2，＋∞)D.(－∞，－2]解析：由f(1)＝，得a2＝，于是a＝，因此f(x)＝()|2x－4|.因为g(x)＝|2x－4|在[2，＋∞)上单调递增，所以f(x)的单调递减区间是[2，＋∞).答案：B8.函数y＝|2x－1|在区间(k－1，k＋1)内不单调，则k的取值范围是()A.(－1，＋∞)B.(－∞，1)C.(－1,1)D.(0,2)解析：由于函数y＝|2x－1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k－1，k＋1)内不单调，所以有k－1＜0＜k＋1，解得－1＜k＜1.答案：C题组四指数函数的综合应用9.若函数f(x)、g(x)分别为R上的奇函数、偶函数，且满足f(x)－g(x)＝ex，则有()A.f(2)f(2)>f(0)＝0且g(0)＝－1，∴g(0)0时，f(x)是周期函数，如图，3欲使方程f(x)＝x＋a有两解，即函数f(x)的图象与直线y＝x＋a有两个不同交点，故a<1，则a的取值范围是(－∞，1).答案：A11.设f(x)＝ax＋b同时满足条件f(0)＝2和对任意x∈R都有f(x＋1)＝2f(x)－1成立.(1)求f(x)的解析式；(2)设函数g(x)的定义域为[－2,2]，且在定义域内g(x)＝f(x)，且函数h(x)的图象与g(x)的图象关于直线y＝x对称，求h(x)；(3)求函数y＝g(x)＋h(x)的值域.解：(1)由f(0)＝2，得b＝1，由f(x＋1)＝2f(x)－1，得ax(a－2)＝0，由ax＞0得a＝2，所以f(x)＝2x＋1.(2)由题意知，当x∈[－2,2]时，g(x)＝f(x)＝2x＋1.设点P(x，y)是函数h(x)的图象上任意一点，它关于直线y＝x对称的点为P′(y，x)，依题意点P′(y，x)在函数g(x)的图象上，即x＝2y＋1，所以y＝log2(x－1)，即h(x)＝log2(x－1)(x∈[，5]).(3)由已知得，y＝log2(x－1)＋2x＋1，且两个函数的公共定义域是[，2]，所以函数y＝g(x)＋h(x)＝log2(x－1)＋2x＋1(x∈[，2]).由于函数g(x)＝2x＋1与h(x)＝log2(x－1)在区间[，2]上均为增函数，当x＝时，y＝2－1，当x＝2时，y＝5，所以函数y＝g(x)＋h(x)(x∈[，2])的值域为[2－1,5].4