高中数学 第二章 点、直线、平面之间的位置关系 10 空间中直线与平面之间的位置关系、平面与平面之间的位置关系课时作业 新人教A版必修2-新人教A版高一必修2数学试题VIP免费

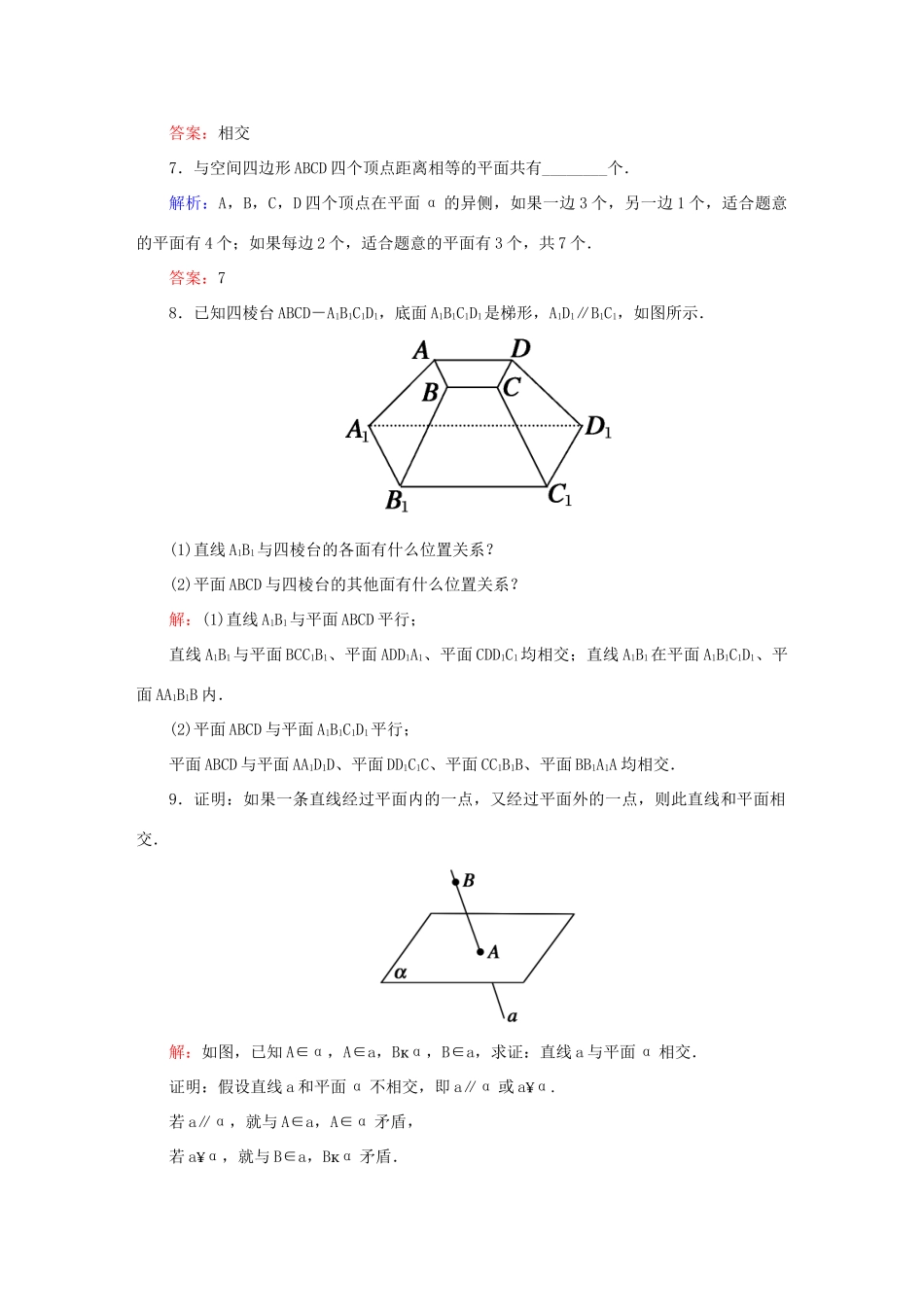
第二章点、直线、平面之间的位置关系10空间中直线与平面之间的位置关系、平面与平面之间的位置关系课时作业新人教A版必修2——基础巩固类——1．直线l与平面α有公共点，则有()A．l∥αB．lαC．l与α相交D．lα或l与α相交答案：D2．平面α与平面β有一个公共点，则平面α与平面β()A．平行B．相交C．异面D．不确定答案：B3．三棱锥的四个面中，任两个面的位置关系是()A．相交B．平行C．异面D．不确定答案：A4．若直线l与平面α不平行，则下列结论正确的是()A．α内的所有直线都与直线l异面B．α内不存在与l平行的直线C．α内的直线与l都相交D．直线l与平面α有公共点答案：D5．平面α∥平面β，直线aα，下列四个命题中，正确命题的个数是()①a与β内的所有直线平行；②a与β内的无数条直线平行；③a与β内的任何一条直线都不垂直；④a与β无公共点．A．1B．2C．3D．4解析：借助于长方体模型，可以举出反例说明①③是错误的；利用面面平行的定义进行判断，则有②④是正确的．答案：B6．若一个平面内的一条直线与另一个平面相交，则这两个平面的位置关系是________．答案：相交7．与空间四边形ABCD四个顶点距离相等的平面共有________个．解析：A，B，C，D四个顶点在平面α的异侧，如果一边3个，另一边1个，适合题意的平面有4个；如果每边2个，适合题意的平面有3个，共7个．答案：78．已知四棱台ABCD－A1B1C1D1，底面A1B1C1D1是梯形，A1D1∥B1C1，如图所示．(1)直线A1B1与四棱台的各面有什么位置关系？(2)平面ABCD与四棱台的其他面有什么位置关系？解：(1)直线A1B1与平面ABCD平行；直线A1B1与平面BCC1B1、平面ADD1A1、平面CDD1C1均相交；直线A1B1在平面A1B1C1D1、平面AA1B1B内．(2)平面ABCD与平面A1B1C1D1平行；平面ABCD与平面AA1D1D、平面DD1C1C、平面CC1B1B、平面BB1A1A均相交．9．证明：如果一条直线经过平面内的一点，又经过平面外的一点，则此直线和平面相交．解：如图，已知A∈α，A∈a，Bα，B∈a，求证：直线a与平面α相交．证明：假设直线a和平面α不相交，即a∥α或aα.若a∥α，就与A∈a，A∈α矛盾，若aα，就与B∈a，Bα矛盾．所以假设不成立，所以直线a和平面α相交．——能力提升类——10．教室内有一根直尺，无论怎样放置，在地面上总有这样的直线与直尺所在的直线()A．异面B．相交C．平行D．垂直解析：若尺子与地面相交，则C不正确；若尺子平行于地面，则B不正确；若尺子放在地面上，则A不正确．所以选D.答案：D11．如果空间的三个平面两两相交，则下列判断正确的是________(填序号)．①不可能只有两条交线；②必相交于一点；③必相交于一条直线；④必相交于三条平行线．解析：空间的三个平面两两相交，可能只有一条交线，也可能有三条交线，这三条交线可能交于一点．答案：①12．如图，平面α、β、γ满足α∥β，α∩γ＝a，β∩γ＝b，判断a与b、a与β的关系并证明你的结论．解：a∥b，a∥β.证明如下：由α∩γ＝a知aα且aγ，由β∩γ＝b知bβ且bγ，∵α∥β，aα，bβ，∴a、b无公共点．又∵aγ且bγ，∴a∥b.∵α∥β，∴α与β无公共点．又aα，∴a与β无公共点，∴a∥β.