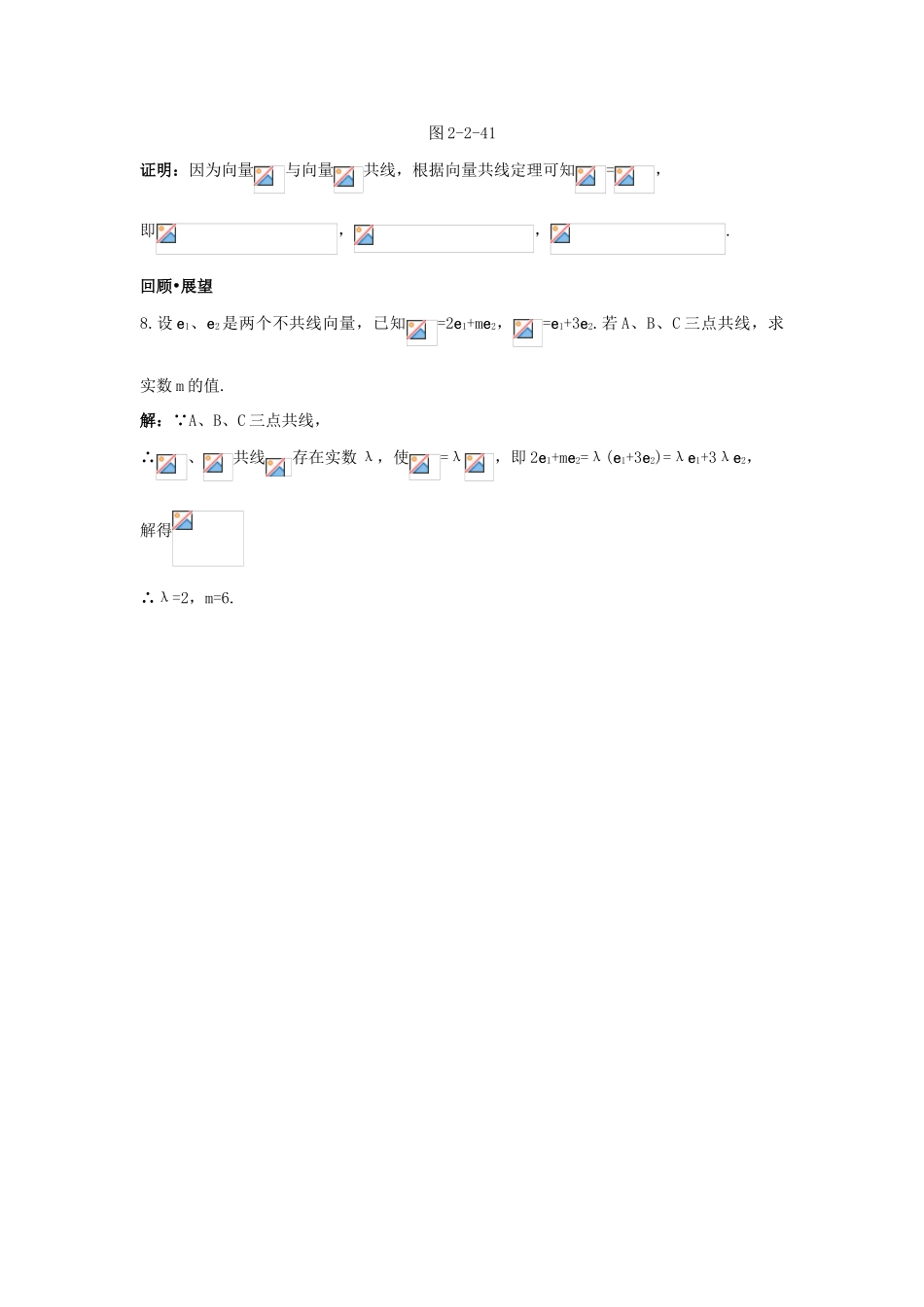
2.2.3向量数乘运算及其几何意义更上一层楼基础•巩固1.[(2a+8b)-(4a-2b)]等于()A.2a-bB.2b-aC.b-aD.a-b思路分析:原式=(a+4b-4a+2b)=(6b-3a)=2b-a.答案:B2.向量a、b共线的有()①a=2e,b=-2e②a=e1-e2,b=-2e1+2e2③a=4e1-e2,b=e1-e2④a=e1+e2,b=2e1-2e2A.①②③B.②③④C.①③④D.①②③④思路分析:对于①②③中的向量a与b,都存在一个相应的实数λ,使a=λb,而④中的两个向量,不存在实数λ使b=λa成立.答案:A3.若O是△ABC内一点,++=0,则O是△ABC的()A.垂心B.重心C.内心D.外心思路分析:∵++=0,∴=-(+).如图,+==-.∴A、O、E三点共线,点D为的中点.∴O为三角形三条中线的交点,是它的重心.答案:B4.设=(a+5b),=-2a+8b,=3(a-b),则共线的三点是()A.A、B、CB.B、C、DC.A、B、DD.A、C、D思路分析:∵+==(-2a+8b)+3(a-b)=a+5b,∴=.又与有公共点B,∴A、B、D三点共线.答案:C综合•应用5.若|a|=m,b与a的方向相反,且|b|=2,则a=__________.思路分析:由,∴|a|=|b|.∵b与a方向相反,∴b与a共线.∴a=b.答案:b6.下列四个命题:①对于实数m和向量a、b,恒有m(a-b)=ma-mb;②对于实数m,n和向量a,恒有(m-n)a=ma-na;③若ma=mb(m∈R),则有a=b;④若ma=na(m、n∈R,a≠0),则m=n.其中正确命题的序号为_________.思路分析:①②满足实数与向量积的运算律.③中若m=0,则ma=mb=0,不一定有a=b;④中由ma=na,则(m-n)a=0,∵a≠0,∴m-n=0.∴m=n.答案:①②④7.如图2-2-41所示,A、B、C是平面内三个点,且A与B不重合,P是平面内任意一点,若点C在直线AB上,则存在实数λ,使得+(1-λ),试证明.图2-2-41证明:因为向量与向量共线,根据向量共线定理可知=,即,,.回顾•展望8.设e1、e2是两个不共线向量,已知=2e1+me2,=e1+3e2.若A、B、C三点共线,求实数m的值.解:∵A、B、C三点共线,∴、共线存在实数λ,使=λ,即2e1+me2=λ(e1+3e2)=λe1+3λe2,解得∴λ=2,m=6.