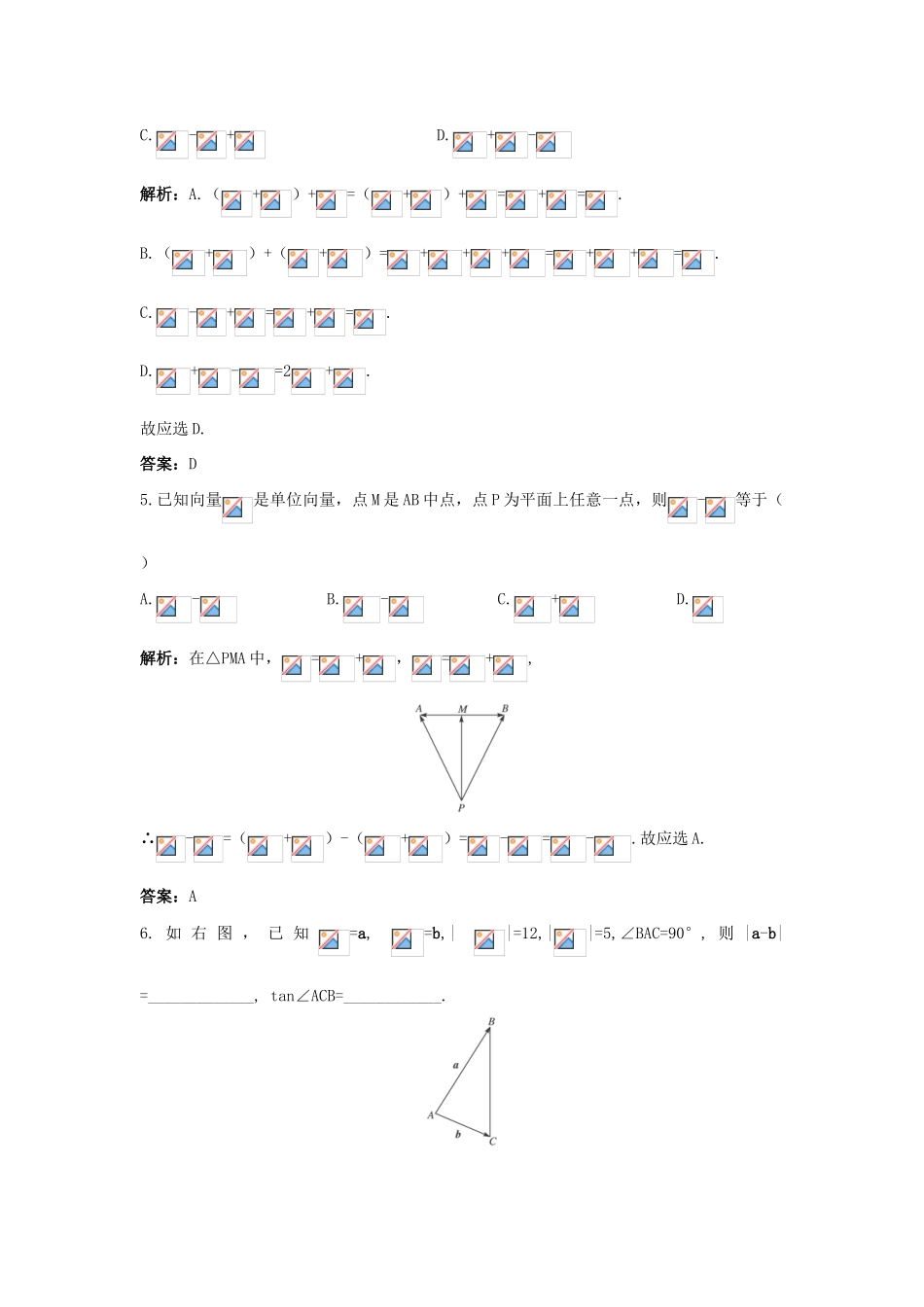
2.2.2向量减法运算及其几何意义课后集训基础达标1.化简下列各式,结果为零向量的个数是()①++②-+-③-+④++-A.1B.2C.3D.4解析:①++=+=0②-+-=++=+=0.③-+=+=0④++-=+=0.∴应选D.答案:D2.如右下图在平行四边形ABCD中,若|+|=|-|,则必有()A.=0B.=0或=0C.ABCD为矩形D.ABCD为正方形解析:由于+=,-=.由条件得:||=||.∵两条对角线相等的平行四边形是矩形.∴应选C.答案:C3.下列各式中,恒成立的是()A.=B.a-a=0C.-=D.++=0答案:D4.下列四个式子中,不能化简为的是()A.(+)+B.(+)+(+)C.-+D.+-解析:A.(+)+=(+)+=+=.B.(+)+(+)=+++=++=.C.-+=+=.D.+-=2+.故应选D.答案:D5.已知向量是单位向量,点M是AB中点,点P为平面上任意一点,则-等于()A.-B.-C.+D.解析:在△PMA中,=+,=+,∴-=(+)-(+)=-=-.故应选A.答案:A6.如右图,已知=a,=b,||=12,||=5,∠BAC=90°,则|a-b|=_____________,tan∠ACB=____________.解析:由于a-b=,∴|a-b|=||=13,tan∠ACB=.答案:13综合运用7.下列等式:①0-a=-a;②-(-a)=a;③a+(-a)=0;④a+0=a;⑤a-b=a+(-b);⑥a+(-a)=0.正确的个数是()A.3B.4C.5D.6解析:⑥错误,应为0.答案:C8.对于任意向量a、b,恒有()A.|a+b|=|a|+|b|B.|a-b|=|a|-|b|C.|a-b|≤|a|+|b|D.|a-b|≤|a|-|b|解析:由向量加减法的三角形法则可得.答案:C9.若O是△ABC内一点,++=0,则O是△ABC的()A.内心B.外心C.垂心D.重心解析:如右图所示,由+=知四边形ADBO为平行四边形,故OE=ED.由已知++=0,故+=,即=,故C、O、E三点共线,且CO=2OE,即O分CE为2∶1.所以O为△ABC的重心.答案:D拓展探究10.证明:对于任意向量a,b都有||a|-|b||≤|a-b|≤|a|+|b|,并指出等号成立的条件.思路分析:这是一个涉及两个向量的重要不等式,证明的关键在于正确分类,逐一解决.证明:(1)当a,b共线时,①a,b(a,b非零)同向时,则|a-b|=||a|-|b||<|a|+|b|;②只有当a,b中至少有一个零时,|a-b|=||a|-|b||=|a|+|b|;③当a,b(a,b非零)反向时,|a-b|=|a|+|b|>||a|-|b||.(2)当a,b不共线时,如右上图,在△ABC中,=a,=b,则=-=a-b.根据三角形中任意两边之差总小于第三边,两边之和总大于第三边可得:||a|-|b||<|a-b|<|a|+|b|.综合(1)(2)可得:对任意向量a,b都有||a|-|b||≤|a-b|≤|a|+|b|.只有当a,b同向或a,b中至少一个为0时,||a|-|b||≤|a-b|中的等号成立;只有当a,b反向或a,b中至少一个为0时,|a-b|≤|a|+|b|中的等号成立.备选习题11.设a,b都是非零向量,(1)若向量a与b反向,则a-b与a的方向_________,且|a-b|_________|a|+|b|;(2)若a与b同向,且|a|>|b|则a-b与a的方向_________且|a-b|_________|a|-|b|.答案:(1)相同=(2)相同=12.(1)当非零向量满足______________条件时,能使a+b平分a与b的夹角;满足______________条件时,能使|a+b|=|a-b|.(2)已知||=|a|,||=b且|a|=|b|=8,∠AOB=60°,则|a+b|=,|a-b|=,a与a+b所在直线的夹角.解析:(1)作=a,=b,以、为邻边作平行四边形,则a+b=,只有当OACB为菱形时,a+b才平分a与b的夹角.只有当平行四边形为矩形时,才能使其两条对角线相等,即|a+b|=|a-b|.(2)作以、为邻边的平行四边形,则=+=a+b,∴|a+b|=2||=2×8×cos30°=;由减法法则知=a-b,∵|a|=|b|=8,∠AOB=60°.∴|a-b|=8,且a+b所在的直线平分a与b的夹角,∴a与a+b所在直线的夹角为30°.答案:(1)|a|=|b|a⊥b(2)830°13.如下图,已知a、b、c分别作出a+b,a+c,a-c,b-c.解:如右图,作=a,=b,=c分别以、为邻边作平行四边形OADB,则=a+b.再分别以、为邻边作平行四边形OAEC,则=a+c.连结AC,则=a-c.再连结,则=b-c.14.如下图,已知O为平行四边形ABCD内一点,OA=a,OB=b,OC=c,求.解:与a、b、c之间难以建立直接的关系,挖掘隐含条件=寻找、a与以及b、c与的关系可间接获解.∵+=,+==,∴+=+,∴=-++=-+=a-b+c.15.一条渔船距对岸4km,以2km/h的速度垂直于对岸的方向划去,到达对岸时,船实际航程为8km,则河水的流速为_________.解析:如右图设表示船垂直于对岸的速度,则由+=知就是渔船实际航行的速度,航行时间为4÷2=2h,在Rt△ABC中,||=2km/h,||=8÷2=4km/h,∴||=km/h.答案:km/h16.如右图所示,5N的重物在两根细绳的支持下处于平衡状态,如果两细绳与水平线的夹角分别是30°和60°,那么两细绳各受力的多少?解:将重力沿两根细绳方向分解,则依题意知,两根细绳的夹角为90°,∴||=||cos60°=5×=2.5(N),||=||cos30°=5×(N).∴两根细绳上承受的拉力大小分别是2.5N和N.