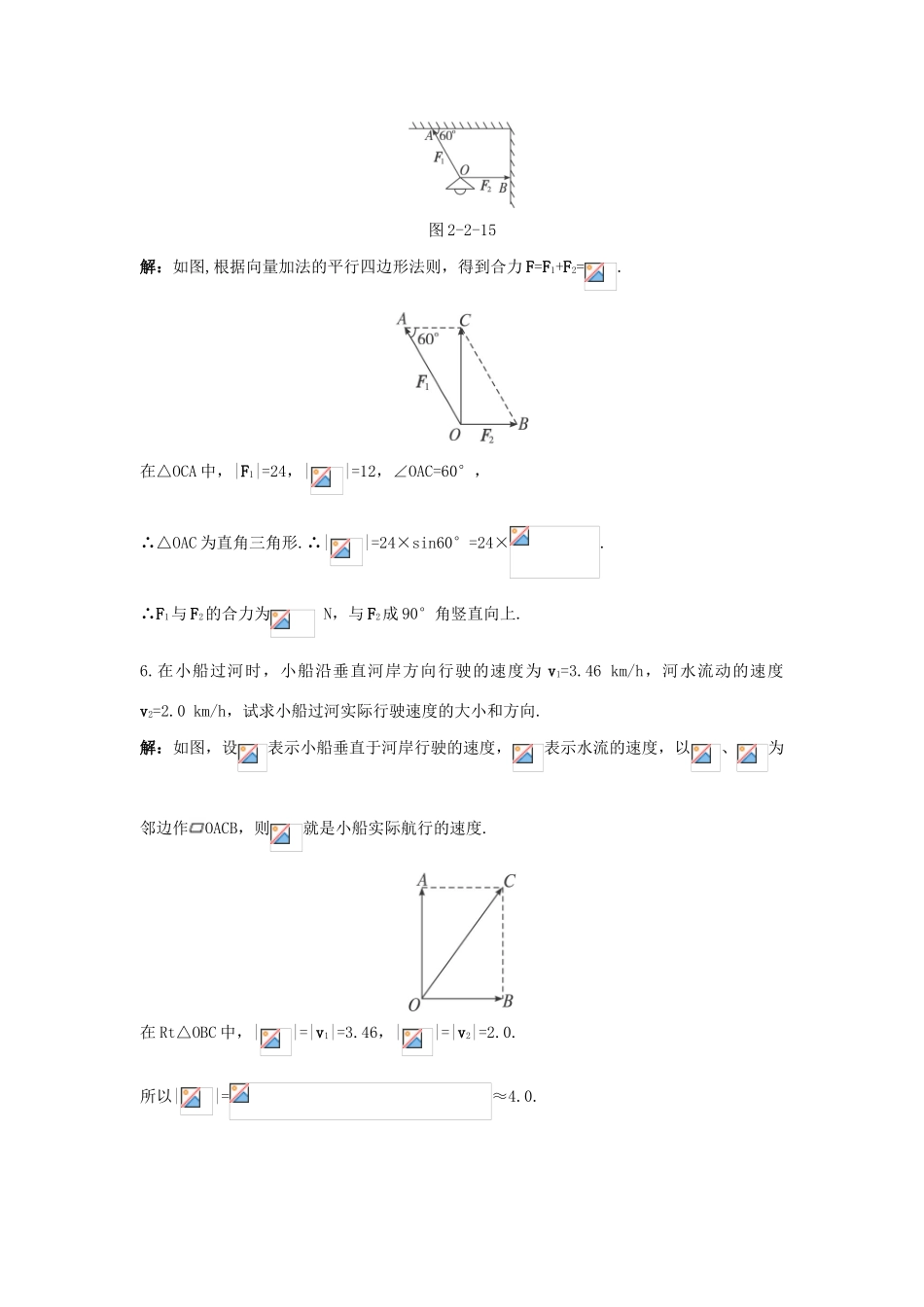
2.2.1向量加法运算及其几何意义更上一层楼基础•巩固1.如图2-2-13,填空:图2-2-13(1)=__________;(2)=_________;(3)=_________;(4)=__________.答案:(1)(2)(3)(4)02.如图2-2-14,已知向量a、b、c不共线,求作a+b+c.图2-2-14解:如图.3.已知向量a、b、c、d分别表示下列位移:“向北10km”“向南5km”“向西10km”“向东5km”.请说明向量a+b,b+b,a+c,a+b+b,a+d+d的意义.解:(1)a+b表示“向北5km”;(2)b+b表示“向南10km”;(3)a+c表示“向西北km”;(4)a+b+b表示“位移为0”;(5)a+d+d表示“向东北km”.4.某人从点A向东位移60m到达点B,又从点B向东偏北30°方向位移50m到达点C,又从点C向北偏西60°方向位移30m到达点D,选用适当的比例尺作图,求点D相对于点A的位置.解:如图2-2-16,构造了三个直角三角形:△CFB,△CED和△DMA.在Rt△CFB中,||=50×sin30°=25,||=50×cos30°=.在Rt△CED中,||=30×cos30°=,||=30×sin30°=15.∴=15+25=40,.∴在Rt△DMA中,=40,=60+.∴||=≈87.tan∠DAM=≈0.5173.由计算器计算得∠DAM=27°18′.∴D在A点东偏北27°18′且距A87米处.综合•应用5.已知图2-2-15,电线AO与天花板的夹角为60°,电线AO所受拉力F1=20N;绳BO与墙壁垂直,所受拉力F2=12N.求F1和F2的合力.图2-2-15解:如图,根据向量加法的平行四边形法则,得到合力F=F1+F2=.在△OCA中,|F1|=24,||=12,∠OAC=60°,∴△OAC为直角三角形.∴||=24×sin60°=24×.∴F1与F2的合力为N,与F2成90°角竖直向上.6.在小船过河时,小船沿垂直河岸方向行驶的速度为v1=3.46km/h,河水流动的速度v2=2.0km/h,试求小船过河实际行驶速度的大小和方向.解:如图,设表示小船垂直于河岸行驶的速度,表示水流的速度,以、为邻边作OACB,则就是小船实际航行的速度.在Rt△OBC中,||=|v1|=3.46,||=|v2|=2.0.所以||=≈4.0.因为tan∠BOC==1.73,所以∠BOC≈60°.所以小船实际航行速度的大小约为4km/h,方向与水流方向约成60°角.7.雨滴在下落一定时间后的运动是匀速的,无风时雨滴下落的速度是4.0m/s.现在有风,风使雨滴以3.0m/s的速度水平向东移动,那么雨滴将以多大的速度着地?这个速度的方向怎样?解:如图,用表示雨滴下落的速度,表示风使雨滴水平向东的速度.以、为邻边作OACB,就是雨滴实际下落的速度.在Rt△OAC中,||=4,||=3,∴||=.∵tan∠AOC==0.75,∴∠AOC≈37°.∴雨滴下降到地面的速度为5m/s,与垂直方向成37°角.回顾•展望8.如图2-2-16,在一场足球比赛中,中场队员在A点位置得球,将球传给位于B点的左边锋,随即快速直向插上.边锋得球后看到对方后卫上前逼抢,于是将球快速横传至门前.球到达C点时前插的中场队员正好赶到,直接射门得分.若BC=20m,∠ABC=37°.图2-2-16(1)求中场队员从传球至射门这一过程中足球的位移;(2)这一过程中中场队员的位移与球的位移是否相等?解:(1)在Rt△ACB中,||=20,由=tan∠ABC,∴||=||tan37°≈20×0.75=15.∴足球的位移为15m,沿垂直球门的方向.(2)这一过程中中场队员的位移与球的位移相等,即=+.