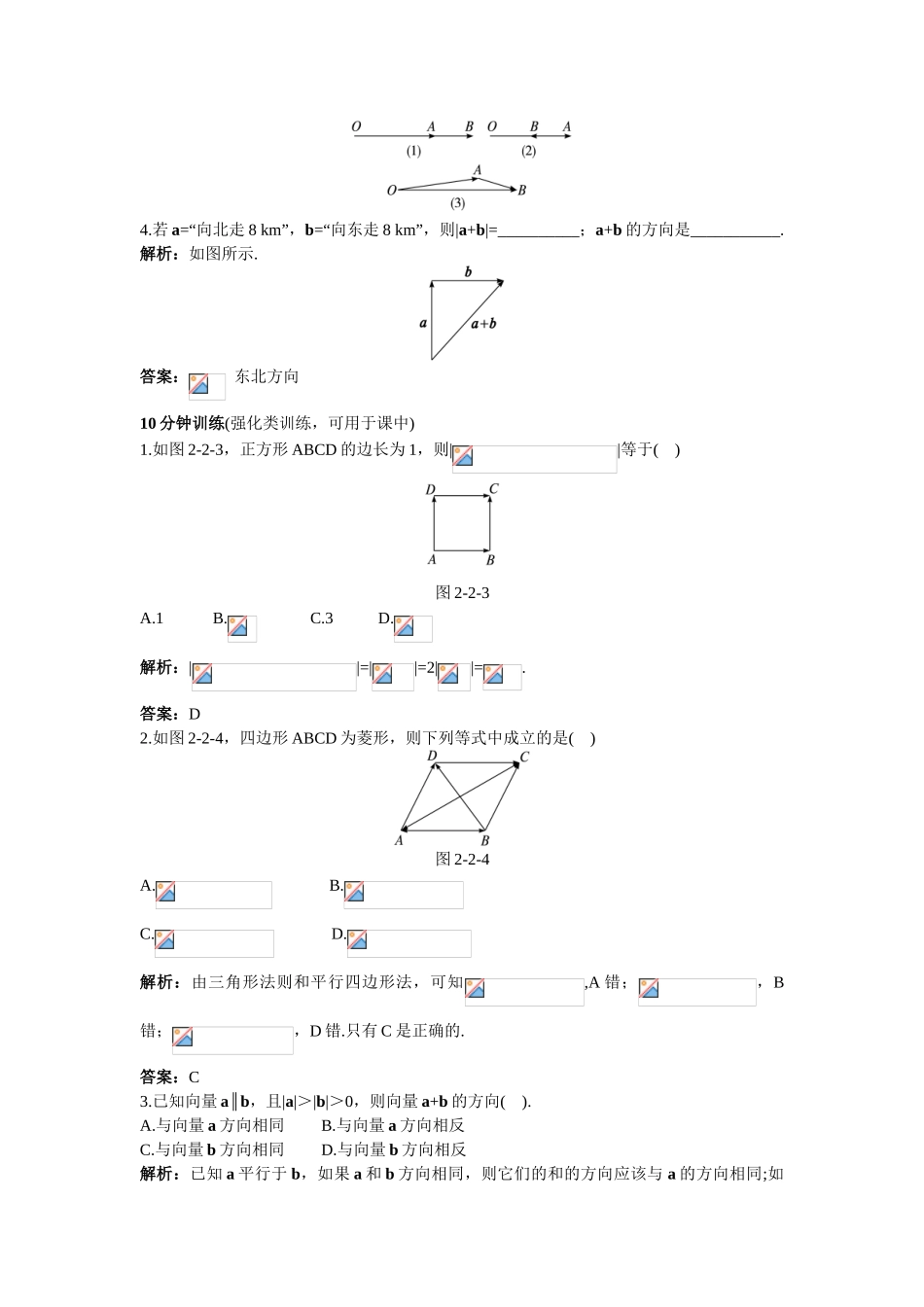
2.2.1向量加法运算及其几何意义5分钟训练(预习类训练,可用于课前)1.如图2-2-1所示,在圆O中,向量、、是()图2-2-1A.有相同起点的向量B.单位向量C.模相等的向量D.相等的向量解析:指定大小和方向后就可以确定一个向量,不能说某些向量是有相同起点的,A错;本题中没有给定向量的长度是1,所以不能说它们是单位向量,B错;这三个向量的方向是不同的,所以不是相等的向量,D错;这三个向量的模都是圆的半径,所以它们的模相等.答案:C2.(1)把平面上所有单位向量的起点平行移动到同一点P,则这些向量的终点构成的几何图形为_____________________.(2)把平行于直线l的所有单位向量的起点平行移动到直线l上的点P,这些向量的终点构成的几何图形为___________________.(3)把平行于直线l的所有向量的起点平行移动到直线l上的点P,这些向量的终点构成的几何图形为___________________.解析:向量是自由向量,根据向量相等,可以把向量的起点平移到同一点.(1)因为单位向量的模都是单位长度,所以同起点时,终点构成单位圆.应填:一个圆.(2)因为平行于直线l的所有单位向量只有两个方向,故这样的单位向量只有两个,起点为P,则终点应为:直线l上与P的距离相等的两个点.(3)因为平行于直线l的向量只有两个方向,但长度不同,任何长度都有,所以终点应为:直线l上的任意一点.答案:(1)一个圆.(2)直线l上与点P的距离相等的两个点.(3)直线l上的任意一点.3.如图2-2-2,试作出向量a与b的和a+b.图2-2-2解析:如图,首先作=a,再作=b,则=a+b.4.若a=“向北走8km”,b=“向东走8km”,则|a+b|=__________;a+b的方向是___________.解析:如图所示.答案:东北方向10分钟训练(强化类训练,可用于课中)1.如图2-2-3,正方形ABCD的边长为1,则||等于()图2-2-3A.1B.C.3D.解析:||=||=2||=.答案:D2.如图2-2-4,四边形ABCD为菱形,则下列等式中成立的是()图2-2-4A.B.C.D.解析:由三角形法则和平行四边形法,可知,A错;,B错;,D错.只有C是正确的.答案:C3.已知向量a∥b,且|a|>|b|>0,则向量a+b的方向().A.与向量a方向相同B.与向量a方向相反C.与向量b方向相同D.与向量b方向相反解析:已知a平行于b,如果a和b方向相同,则它们的和的方向应该与a的方向相同;如果它们的方向相反,因为a的模大于b的模,所以它们的和仍然与a的方向相同.答案:A4.如图2-2-5所示,已知向量a,b,c,d,求向量a+b+c+d.图2-2-5解:在空间中任取一点O,作=a,=b,=c,=d,则=a+b+c+d.5.如图2-2-6所示,已知向量a、b、c,求作向量a+b+c.图2-2-6解:如图,首先作=b,再作=a,=c则=a+b+c.30分钟训练(巩固类训练,可用于课后)1.已知平行四边形ABCD,设()+()=a,而b是一非零向量,则下列结论正确的有()①a∥b②a+b=a③a+b=b|④a+b|<|a|+|b|A.①③B.②③C.②④D.①②解析:在平行四边形ABCD中,=0,=0,所以a为零向量,零向量和任何向量都平行,零向量和任意向量的和等于这个向量本身,所以①③正确.答案:A2.向量a、b都是非零向量,下列说法不正确的是()A.向量a与b同向,则向量a+b与a的方向相同B.向量a与b同向,则向量a+b与b的方向相同C.向量a与b反向,且|a|<|b|,则向量a+b与a的方向相同D.向量a与b反向,且|a|>|b|,则向量a+b与a的方向相同解析:向量a与b反向,且|a|<|b|,则向量a+b的方向应该和模较大的向量相同,即和b的方向相同,所以C错.答案:C3.a、b为非零向量,且|a+b|=|a|+|b|,则下列说法正确的是()A.a∥b,且a与b方向相同B.a、b是共线向量C.a=-bD.a、b无论什么关系均可解析:当两个非零向量a与b不共线时,a+b的方向与a、b的方向都不相同,且|a+b|<|a|+|b|;向量a与b同向时,a+b的方向与a、b的方向都相同,且|a+b|=|a|+|b|;向量a与b反向且|a|<|b|时,a+b的方向与b的方向相同(与a方向相反),且|a+b|=|b|-|a|.答案:A4.在平行四边形ABCD中,下列式子:①;②;③;④;⑤;⑥.其中不正确的个数是()A.1B.2C.4D.6解析:,所以⑥错,其他各项都是正确的.答案:A5.下列命题①如果非零向量a与b的方向相同或相反,那么a+b的方向必与a、b之一的方向相同;ABC②△中,必有=0;③若=0,则A、B、C为一个三角形的三个顶点;④若a、b均为非...