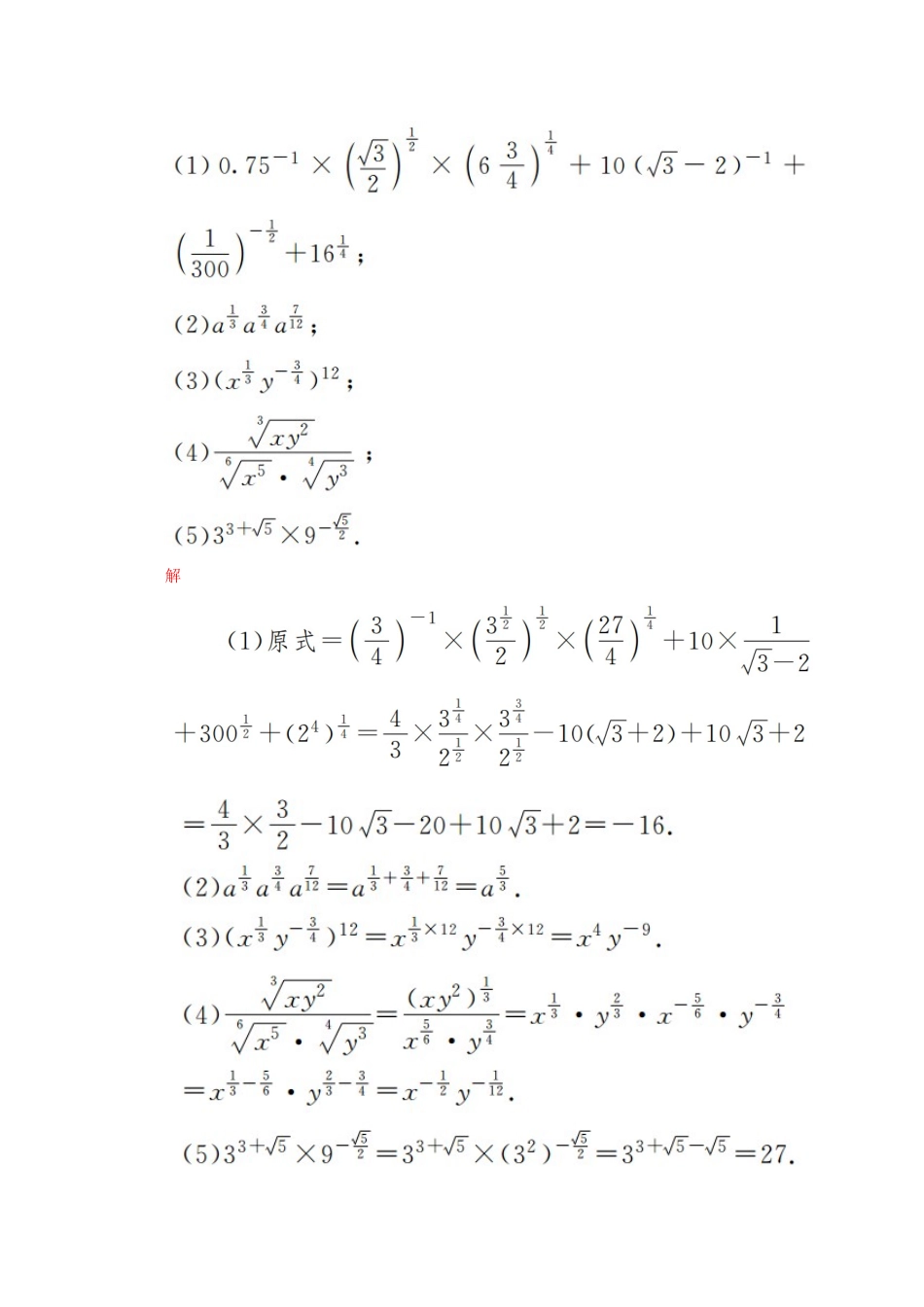课时1实数指数幂及其运算知识点一整数指数幂的运算1.设m,n是整数,a,b是实数(ab≠0),则下列各式中正确的有()①a·a·a=a3;②a0=1;③a-1=;④a4·a-3=a;⑤(am)n=amn;⑥(ab)n=an·bn.A.6个B.5个C.4个D.3个答案A解析由整数指数幂的性质,可知这6个选项都正确.故选A.2.若10x=3,10y=4,则10x-y=________,10x+y=________.答案12解析10x-y==,10x+y=10x·10y=12.知识点二根式与分数指数幂的互化答案C解析4.用分数指数幂形式表示:=________.答案解析5.(a>0,b>0)用分数指数幂可表示为________.答案解析解法一:(由内向外化)解法二:(由外向内化)知识点三实数指数幂的运算6.计算(或化简)下列各式:解易错点化简忽略条件而致误7.计算:+.易错分析注意≠1-,而是=|1-|=-1.其出错原因是=a(a∈R)成立的条件是n为正奇数,如果n为正偶数,那么=|a|.正解+=(1+)+|1-|=1++-1=2.一、选择题1.+(a-4)0有意义,则a的取值范围是()A.a≥2B.2≤a<4或a>4C.a≠2D.a≠4答案B解析要使原式有意义,需满足:,解得2≤a<4或a>4.2.计算(n∈N*)的结果为()A.B.22n+5C.2n2-2n+6D.2n-7答案D解析原式===2n-7.3.当有意义时,化简-的结果为()A.2x-5B.-2x-1C.-1D.5-2x答案C解析由有意义得x≤2.故-=|x-2|-|x-3|=(2-x)-(3-x)=-1.答案A解析5.计算的值等于()A.1+B.1-C.2+D.2-答案D解析∵====1-,∴原式=×2=2-.二、填空题6.设α,β是方程5x2+10x+1=0的两个根,则2α·2β=________,(2α)β=________.答案解析利用一元二次方程根与系数的关系,得α+β=-2,αβ=.则2α·2β=2α+β=2-2=,(2α)β=2αβ=.7.计算:-0+-0.5+=________.(e为自然对数的底数)答案e+解析原式=+1-1+2×0.5+e-=e+.答案2解析三、解答题9.已知a=2,b=5,求·的值.解a6b-6-6a3b-1+9b4=(a3b-3-3b2)2,由a=2,b=5,得a3b-3<3b2.∴原式=·=-=-=-b2.∵b=5,故原式=-50.解