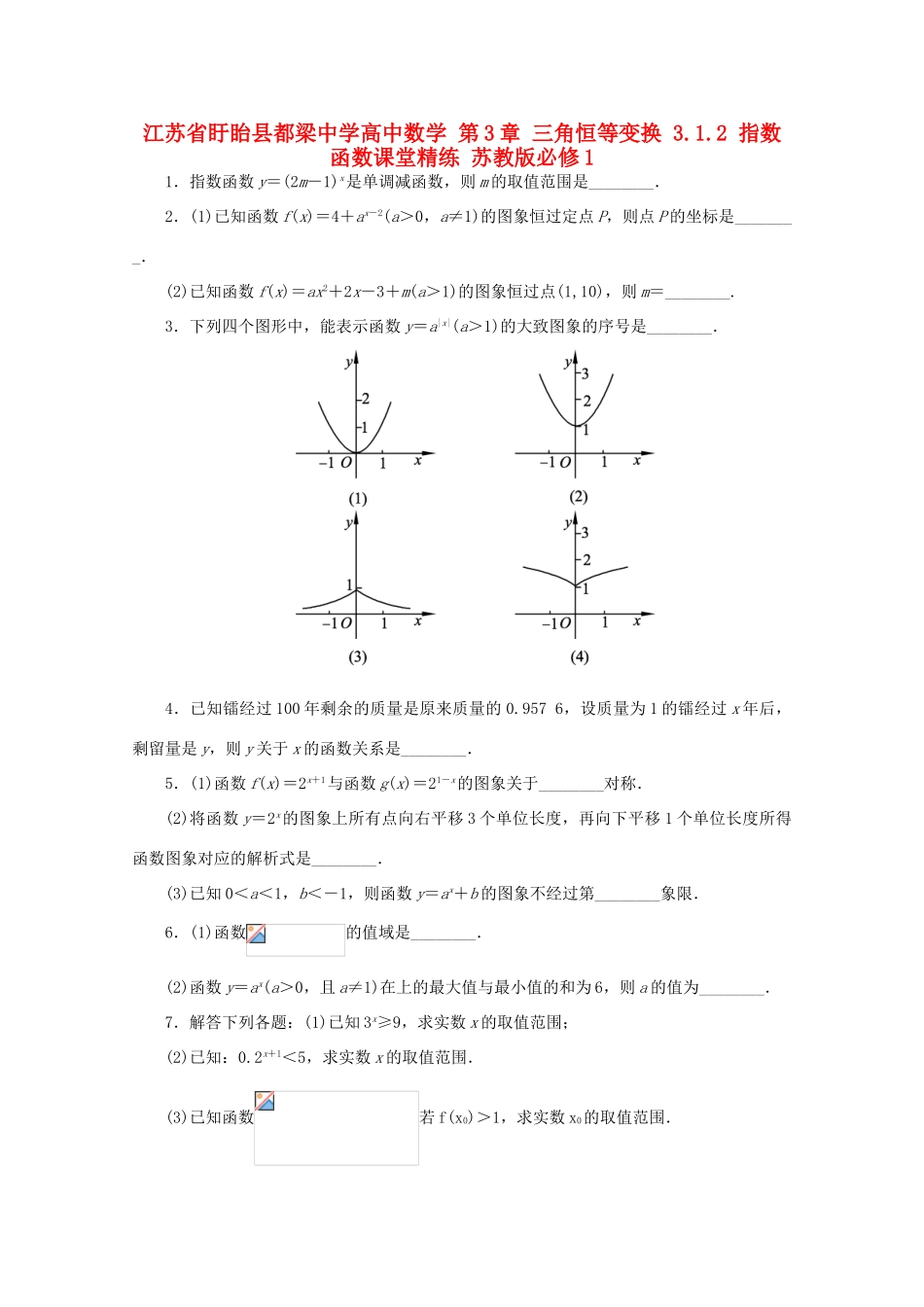
江苏省盱眙县都梁中学高中数学第3章三角恒等变换3.1.2指数函数课堂精练苏教版必修11.指数函数y=(2m-1)x是单调减函数,则m的取值范围是________.2.(1)已知函数f(x)=4+ax-2(a>0,a≠1)的图象恒过定点P,则点P的坐标是________.(2)已知函数f(x)=ax2+2x-3+m(a>1)的图象恒过点(1,10),则m=________.3.下列四个图形中,能表示函数y=a|x|(a>1)的大致图象的序号是________.4.已知镭经过100年剩余的质量是原来质量的0.9576,设质量为1的镭经过x年后,剩留量是y,则y关于x的函数关系是________.5.(1)函数f(x)=2x+1与函数g(x)=21-x的图象关于________对称.(2)将函数y=2x的图象上所有点向右平移3个单位长度,再向下平移1个单位长度所得函数图象对应的解析式是________.(3)已知0<a<1,b<-1,则函数y=ax+b的图象不经过第________象限.6.(1)函数的值域是________.(2)函数y=ax(a>0,且a≠1)在上的最大值与最小值的和为6,则a的值为________.7.解答下列各题:(1)已知3x≥9,求实数x的取值范围;(2)已知:0.2x+1<5,求实数x的取值范围.(3)已知函数若f(x0)>1,求实数x0的取值范围.参考答案1.解析:由题意知,0<2m-1<1,∴.2.(1)(2,5)(2)9解析:函数的图象随自变量x的变化而变化,但恒有当x=2时,f(2)=4+a0=5,∴P(2,5).(2)∵f(x)恒过点(1,10),∴把(1,10)点代入函数解析式有:,即a0+m=10,∴m=9.3.(2)解析:函数f(|x|)是偶函数,应先画出x≥0时f(x)的图象,然后沿y轴翻折过去,得到x<0时的函数图象,当x≥0时,y=a|x|=ax图象过(0,1)点,a>1,在第一象限,图象下凸,是单调增函数.∴(2)符合.4.解析:设镭一年放射掉其质量的t%,则0.9576=1·(1-t%)100∴,∴.5.(1)y轴(2)y=2x-3-1(3)一解析:(1)∵g(x)=21-x的图象关于y轴对称的图象对应的函数为f(x)=2x+1,即f(-x)=g(x)与f(x)关于y轴对称,故填y轴.(2)y=2x的图象向右平移3个单位长度,得y=2x-3的图象,再向下平移1个单位长度,得函数y=2x-3-1的图象.(3)∵0<a<1,b<-1.∴y=ax+b的图象如下图所示.由图象知,函数y=ax+b的图象不过第一象限.6.(1)[0,4)(2)2解析:(1)∵4x>0,∴-4x<0,∴0≤16-4x<16.∴0≤y<4.(2)∵y=ax是单调函数,∴最大值与最小值在1,2处取得,∴f(1)+f(2)=6.即a2+a=6,解得a=2或a=-3,又a>0且a≠1,∴a=2.7.解:(1)∵3>1,∴函数y=3x在R上是单调增函数,由3x≥9=32,得x≥2,即x的取值范围是[2,+∞).(2)∵0<0.2<1,∴指数函数y=0.2x在R上是单调减函数.∵,∴0.2x+1<0.2-1,∴x+1>-1,∴x>-2,即x的取值范围是(-2,+∞).(3)当x0≤0时,f(x0)=2-x0-1>1,∴2-x0>2,-x0>1,x0<-1;当x0>0时,令,得x0>1.综上可知,x0的取值范围是(-∞,-1)∪(1,+∞).