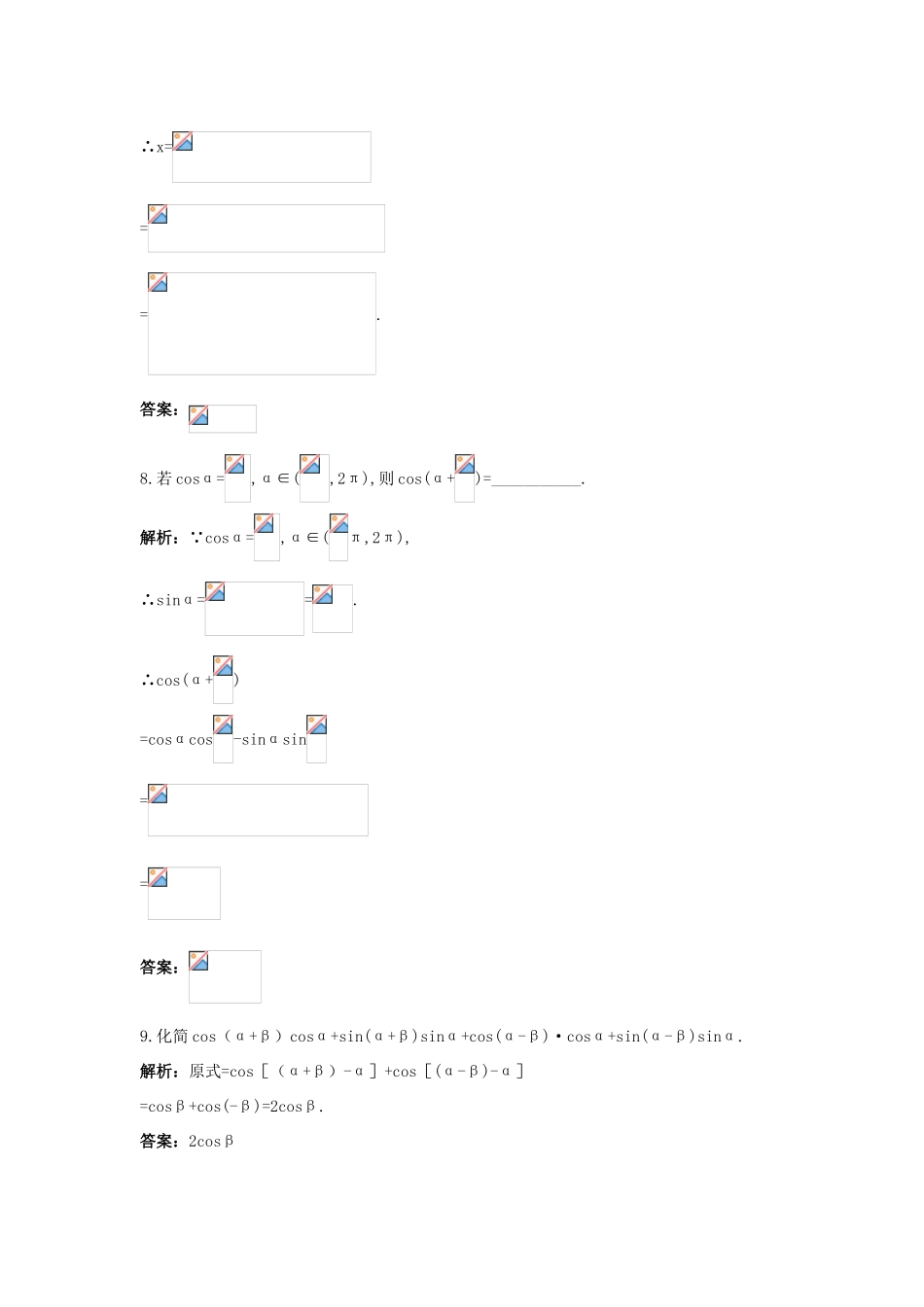
高中数学第3章三角恒等变换3.1.1两角和与差的余弦课后导练苏教版必修4基础达标1.下列等式一定成立的是()A.cos(α-β)=cosα-cosβB.cos(α-β)=cosα+cosβC.cos(-α)=cosαD.cos(-α)=sinα解析:本题是对差角的余弦公式的考查.直接运用公式可知D正确.答案:D2.cos24°cos54°+sin24°sin54°的值是()A.0B.C.D.解析:这是差角余弦公式的逆用,cos24°cos54°+sin24°·sin54°=cos(24°-54°)=cos(-30°)=cos30°=.故选择C.答案:C3.cosα+sinα化简的结果可以是()A.cos(-α)B.2cos(-α)C.cos(-α)D.2cos(-α)解析:cosα+3sinα=2(cosα+sinα)=2(coscosα+sinsinα)=2cos(-α),故答案选B.答案:B4.cos75°-cos15°的值等于()A.B.C.D.解析:cos75°-cos15°=cos(45°+30°)-cos(45°-30°)=cos45°cos30°-sin45°sin30°-cos45°cos30°-sin45°sin30°=-2sin45°sin30°=-,故选择C.答案:C5.设α∈(0,),若sinα=,则cos(α+)等于()A.B.C.D.-解析:sinα=,且α∈(0,),∴cosα=.∴cos(α+)=×(cosαcos-sinαsin)=(×-×)=.答案:B6.cos345°=__________________.解析:cos345°=cos(-15°+360°)=cos(-15°)=cos15°=cos(45°-30°)=cos45°cos30°+sin45°sin30°=.答案:7.若cos15°=xcos105°,则x=___________.解析:∵cos15°=xcos105°∴x===.答案:8.若cosα=,α∈(,2π),则cos(α+)=___________.解析:∵cosα=,α∈(π,2π),∴sinα==.∴cos(α+)=cosαcos-sinαsin==答案:9.化简cos(α+β)cosα+sin(α+β)sinα+cos(α-β)·cosα+sin(α-β)sinα.解析:原式=cos[(α+β)-α]+cos[(α-β)-α]=cosβ+cos(-β)=2cosβ.答案:2cosβ10.在△ABC中,已知sinA=,A为钝角,cosB=,求cos(A+B)的值.解析:∵sinA=,A为钝角,∴cosA=-.又∵在△ABC中,A为钝角,∴B一定为锐角且cosB=,∴sinB=.∴cos(A+B)=cosAcosB-sinAsinB=-×-×=.答案:综合运用11.若sinαsinβ=1,则cos(α+β)的值为()A.0B.1C.-1D.±1解析:sinαsinβ=1可知,sinα=sinβ=1或sinα=sinβ=-1.当sinα=sinβ=1时,cosα=cosβ=0,cos(α+β)=cosαcosβ-sinαsinβ=-1.当sinα=sinβ=-1时,cosα=cosβ=0,cos(α+β)=cosαcosβ-sinαsinβ=-1.故选择C.答案:C12.若A、B、C是△ABC的三个内角,且sinA=,cosB=,那么cosC的值是()A.B.C.或D.不确定解析:由条件可得sinB=,cosA=±.∵sinA=<=sinB,且A+B<180°,∴A<B即A为锐角,∴cosA=.∴cosC=cos[π-(A+B)]=-cos(A+B)=-(cosAcosB-sinAsinB)=.故选择A.答案:A13.函数y=4sin(3x+)+3cos(3x+)的最小正周期是()A.6πB.2πC.D.解析:y=4sin(3x+)+3cos(3x+)=5[sin(3x+)+cos(3x+)].令sinφ=,cosφ=,∴y=5[sinφsin(3x+)+cosφcos(3x+)]=5cos(3x+-φ).∴其最小正周期为,故选择C.答案:C14.已知sin(-α)=,<α<,则cosα=__________________.解析:∵sin(-α)=,∴sin(α-)=.又∵<α<,∴0<α-<,∴cos(α-)>0.∴cos(α-)=.cosα=cos[(α-)+]=cos(α-)·cos-sin(α-)·sin=××=.答案:15.已知cos(α-β)=-,α-β∈(,π),cos(α+β)=,α+β∈(π,2π),求cos2β.解析:∵cos(α-β)=-,α-β∈(,π),∴sin(α-β)=,又∵cos(α+β)=,α+β∈(π,2π),∴sin(α+β)=-.∵2β=(α+β)-(α-β),∴cos2β=cos[(α+β)-(α-β)]=cos(α+β)cos(α-β)+sin(α+β)sin(α-β)=×(-)+(-)×=-1.答案:-1拓展探究16.已知cos(+α)=,sin(-β)=,且0<α<<β<π,求cos(β-α)的值.思路分析:观察到sin(-β)=sin(+β)=,β-α=(+β)-(+α)解:∵0<α<<β<π,∴<+α<<+β<.∵cos(+α)=<0,∴<+α<,∴sin(+α)=.∵sin(-β)=sin[π-(+β)]=sin(+β)=>0,∴<+β<π.∴cos(+β)=∴cos(β-α)=cos[(+β)-(+α)]=cos(+β)cos(+α)+sin(+β)·sin(+α)=-×()+×()=.