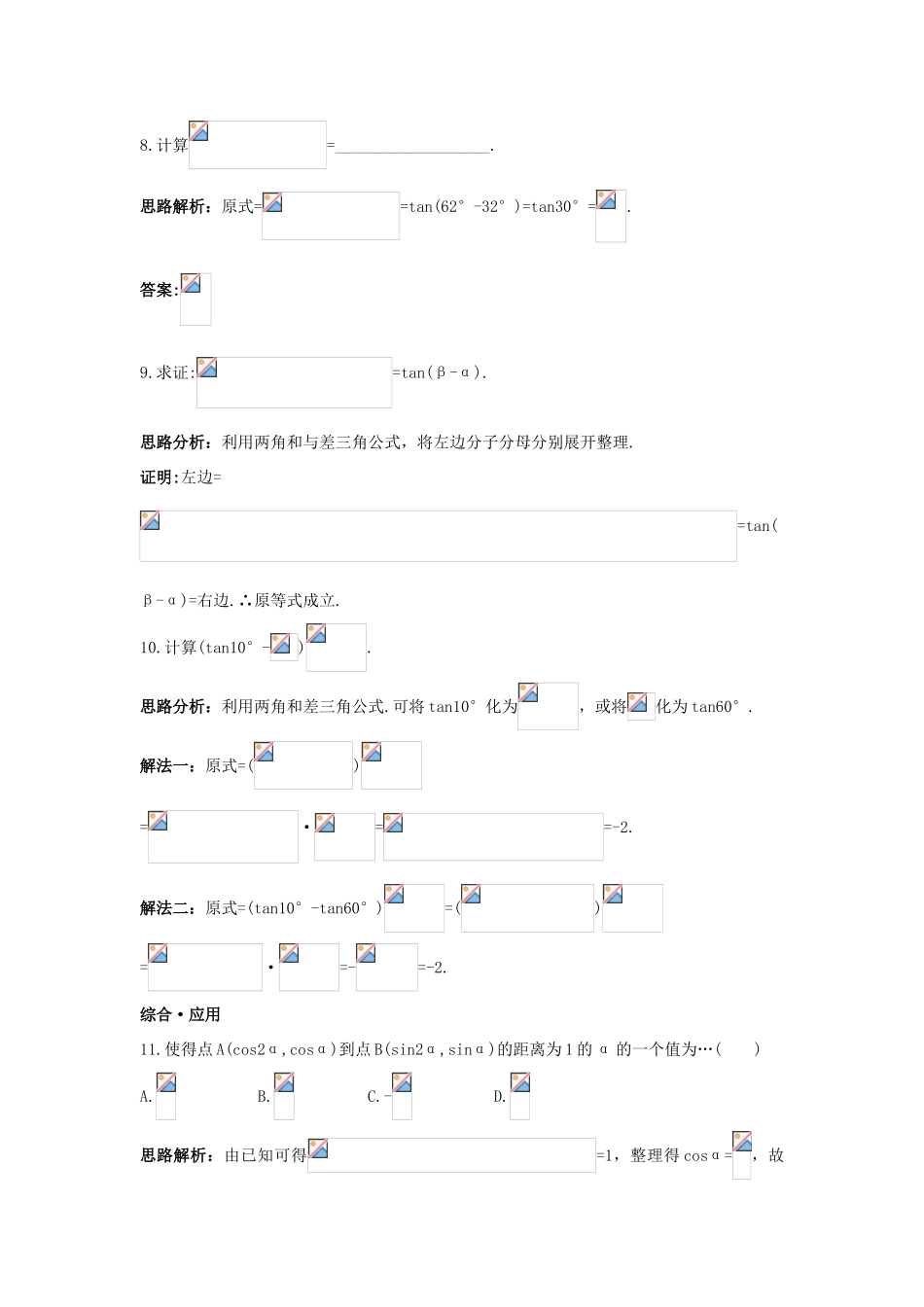
高中数学第3章三角恒等变换3.1两角和与差的三角函数达标训练苏教版必修4基础·巩固1.sin15°cos165°的值等于()A.B.-C.D.-思路解析:sin15°cos165°=sin15°cos(180°-15°)=-sin15°cos15°=-(sin15°cos15°+cos15°sin15°)=-sin30°=-.答案:B2.若sin(α-β)cosα-cos(α-β)sinα=m且β为第三象限角,则cosβ为()A.B.-C.D.-思路解析:由题意知sin(α-β-α)=sin(-β)=m,∴sinβ=-m.又∵β为第三象限角,∴cosβ=-=-.本题也可用排除法,由β为第三象限角,排除A、C,又m2-1<0,故选B.答案:B3.若tanα=2,tan(β-α)=3,则tan(β-2α)的值是()A.-1B.-C.D.思路解析:tan(β-2α)=tan[(β-α)-α]===.答案:D4.若=,则cot(45°+A)等于()A.B.C.D.思路解析:由=,得=tan(45°-A)=,∴cot(45°+A)=tan(45°-A)=.答案:C5.已知α∈(,2π),且tan(+α)=,则cos(α-)的值是()A.-B.C.-D.思路解析:∵tan(+α)=-cotα=,∴tanα=-,α∈(,2π).∴cosα==,sinα=cosα·tanα=×(-)=-.∴cos(α-)=cosαcos+sinαsin=×(-)+(-)×=-.答案:C6.cos285°=__________________.思路解析:法一:原式=cos(180°+105°)=-cos105°=-cos(60°+45°)=-cos60°cos45°+sin60°·sin45°=-×+×=.法二:原式=cos(360°-75°)=cos75°=cos(30°+45°)=cos30°cos45°-sin30°sin45°=×-×=.答案:7.化简cos44°sin166°+sin44°cos166°=________________.思路解析:原式=cos44°sin14°-cos14°sin44°=sin(14°-44°)=sin(-30°)=-.答案:-8.计算=___________________.思路解析:原式==tan(62°-32°)=tan30°=.答案:9.求证:=tan(β-α).思路分析:利用两角和与差三角公式,将左边分子分母分别展开整理.证明:左边==tan(β-α)=右边.∴原等式成立.10.计算(tan10°-).思路分析:利用两角和差三角公式.可将tan10°化为,或将化为tan60°.解法一:原式=()=·==-2.解法二:原式=(tan10°-tan60°)=()=·=-=-2.综合·应用11.使得点A(cos2α,cosα)到点B(sin2α,sinα)的距离为1的α的一个值为…()A.B.C.-D.思路解析:由已知可得=1,整理得cosα=,故选择A.此外,本题也可以用反代法解题,即将选项一一代入后验证.答案:A12.化简sin(x+60°)+2sin(x-60°)-cos(120°-x)=______________.思路解析:原式=sinx+cosx+2(sinx-cosx)-(-cosx+sinx)=sinx+cosx+sinx-cosx+cosx-sinx=0.答案:013.化简tan(-θ)+tan(+θ)+tan(-θ)tan(+θ)=__________________.思路解析:原式=tan(-θ++θ)[1-tan(-θ)tan(+θ)]+tan(-θ)tan(+θ)=tan-tantan(-θ)tan(+θ)+tan(-θ)tan(+θ)=.答案:14.已知sinα=,cosβ=-,且α、β为相邻象限的角,求sin(α+β)和sin(α-β)的值.思路分析:应用两角和、差公式.解:∵sinα=>0,cosβ=-且α、β为相邻象限的角,∴α、β分别在一、二象限或二、三象限.(1)当α、β分别在一、二象限时,cosα=,sinβ=,∴sin(α+β)=sinαcosβ+cosαsinβ=×(-)+×=,sin(α-β)=sinαcosβ-cosαsinβ=-.(2)当α、β分别在二、三象限时,cosα=-,sinβ=-,可求sin(α+β)=,sin(α-β)=-.综上,sin(α+β)=,sin(α-β)=-.回顾·展望15.(2006福建高考)已知α∈(,π),sinα=,则tan(α+)等于()A.B.7C.-D.-7思路解析:∵α∈(,π),sinα=,∴cosα=-.∴tanα==-.而tan(α+)==.答案:A16.(2006重庆高考)已知α、β∈(,π),sin(α+β)=-,sin(β-)=,则cos(α+)=________.思路解析:∵α、β∈(,π),∴α+β∈(,2π),β-∈(,).∴cos(α+β)==,cos(β-)=-.∴cos(α+)=cos[(α+β)-(β-)]=cos(α+β)cos(β-)+sin(α+β)sin(β-)=×(-)+(-)×=-.答案:-17.(2006江苏高考)cot20°cos10°+sin10°tan70°-2cos40°=_________________.思路解析:cot20°cos10°+sin10°tan70°-2cos40°=tan70°cos10°+sin10°tan70°-2cos40°=tan70°(cos10°+sin10°)-2cos40°=2tan70°(cos10°+sin10°)-2cos40°=2tan70°(sin30°cos10°+cos30°sin10°)-2cos40°=2tan70°sin40°-2cos40°==2.答案:218.(2006全国高考)已知向量a=(sinθ,1),b=(1,cosθ),-<θ<.(1)若a⊥b,求θ;(2)求|a+b|的最大值.思路分析:由a⊥b可得关于θ的三角方程,从而根据角的范围求出θ;(2)|a+b|用关于θ的代数式表示出来,利用三角函数的性质求最值.解:(1)若a⊥b,则有sinθ+cosθ=0,即tanθ=-1,又-<θ<,所以θ=-.(2)由a=(sinθ,1),b=(1,cosθ)得a+b=(sinθ+1,1+cosθ),|a+b|=,又-<θ<,则当sin(θ+)=1时,|a+b|取最大值,即当θ=时,|a+b|取最大值+1.