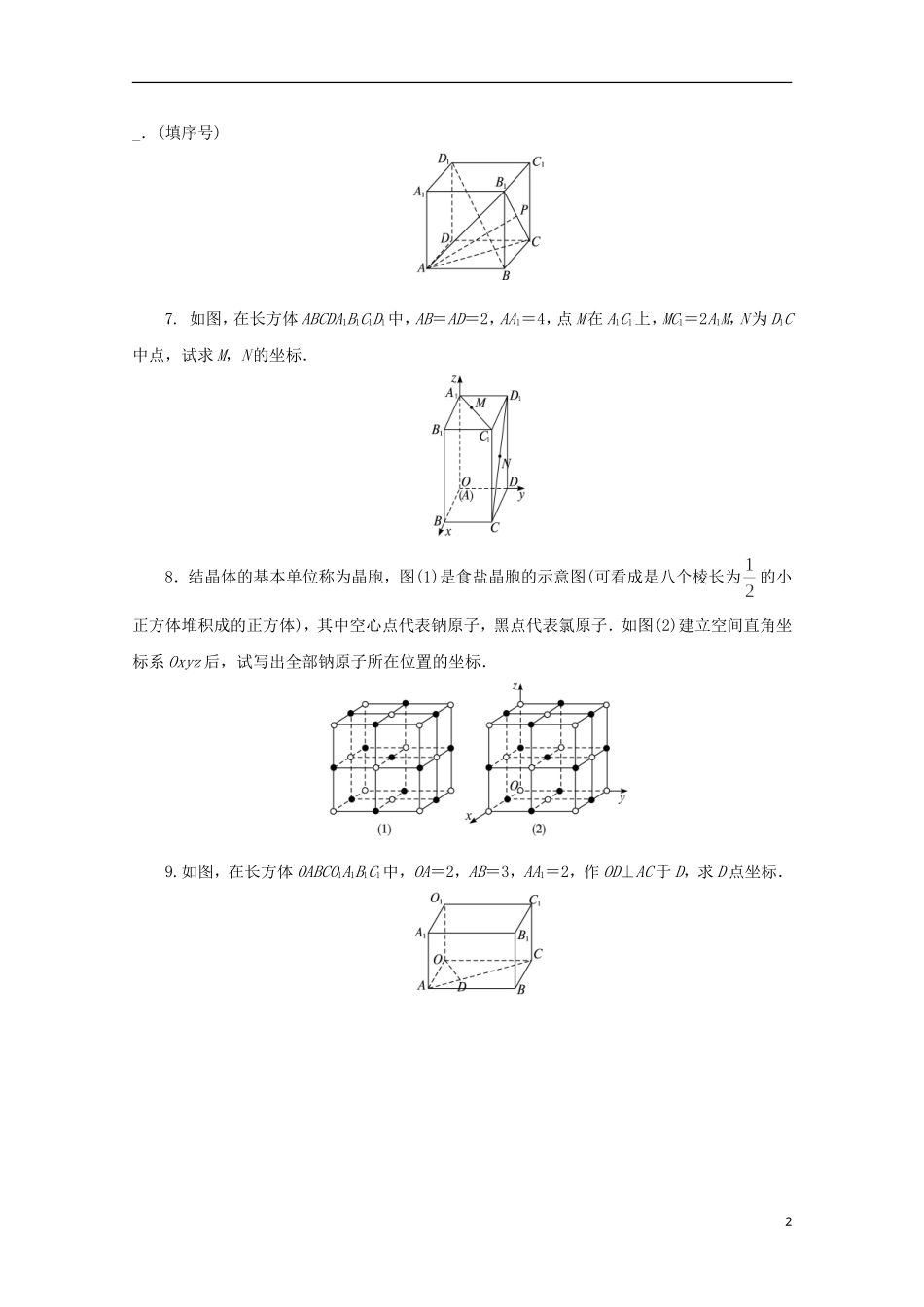
江苏省盱眙县都梁中学高中数学第2章平面解析几何初步2.3.1空间直角坐标系课堂精练苏教版必修21.点A(-1,2,1)在x轴上的投影和在xOy平面上的投影分别为__________.2.以正方体ABCDA1B1C1D1的棱AB,AD,AA1所在的直线为坐标轴建立空间直角坐标系,且正方体的棱长为一个单位长度,则棱CC1中点的坐标为______.3.有一个棱长为1的正方体,对称中心在原点且每一个面平行于坐标平面,给出以下各点:A(1,0,1),B(-1,0,1),,,,.则位于正方体之外的点是__________.4.在平面直角坐标系中,点P(x,y)的几种特殊的对称点的坐标如下:(1)关于原点的对称点是P′(-x,-y);(2)关于x轴的对称点是P″(x,-y);(3)关于y轴的对称点是P(-x,y).那么,在空间直角坐标系中,点P(x,y,z)的几种特殊的对称点坐标为:(1)关于原点的对称点P1是__________;(2)关于横轴(x轴)的对称点P2是__________;(3)关于纵轴(y轴)的对称点P3是__________;(4)关于竖轴(z轴)的对称点P4是__________;(5)关于xOy坐标平面的对称点P5是__________;(6)关于yOz坐标平面的对称点P6是__________;(7)关于zOx坐标平面的对称点P7是__________.5.如图所示,点P′在x轴正半轴上,OP′=2,PP′在xOz平面上,且垂直于x轴,PP′=1,则点P与P′的坐标分别为__________.6.如图所示,正方体ABCDA1B1C1D1棱长为1,以D为原点,射线DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系,若点P在侧面BCC1B1及其边界上运动,并总是保持AP⊥BD1,则下列的点P坐标①(1,1,1),②(0,1,0),③(1,1,0),④(0,1,1),⑤中正确的是_________1_.(填序号)7.如图,在长方体ABCDA1B1C1D1中,AB=AD=2,AA1=4,点M在A1C1上,MC1=2A1M,N为D1C中点,试求M,N的坐标.8.结晶体的基本单位称为晶胞,图(1)是食盐晶胞的示意图(可看成是八个棱长为的小正方体堆积成的正方体),其中空心点代表钠原子,黑点代表氯原子.如图(2)建立空间直角坐标系Oxyz后,试写出全部钠原子所在位置的坐标.9.如图,在长方体OABCO1A1B1C1中,OA=2,AB=3,AA1=2,作OD⊥AC于D,求D点坐标.2参考答案1.(-1,0,0)(-1,2,0)点A(-1,2,1)在x轴上的投影和在xOy平面上的投影分别为(-1,0,0),(-1,2,0).2.3.A,B,F∵棱长为1的正方体的对称中心为坐标原点,∴正方体表面上每个点的坐标都满足,,∴点A,B,F在正方体之外.4.(1)(-x,-y,-z)(2)(x,-y,-z)(3)(-x,y,-z)(4)(-x,-y,z)(5)(x,y,-z)(6)(-x,y,z)(7)(x,-y,z)5.(2,0,1),(2,0,0)由P′在x轴正半轴上,且OP′=2,∴P′(2,0,0).∵PP′⊥x轴,且PP′=1,PP′在xOz平面上,∴P(2,0,1).6.①②⑤由点P为动点,而BD1是定线段,可分析探索一个过点A且与BD1垂直的平面.连结AB1,B1C,AC,由BD1⊥AB1,BD1⊥AC,从而得BD1⊥面AB1C,又由点P在侧面BCC1B1上运动知,点P的轨迹为线段B1C.故应填①②⑤.7.解:A1(0,0,4),C1(2,2,4).∵MC1=2A1M,∴.过M向A1B1作垂线,垂足为P,过M向A1D1作垂线,垂足为Q,则,,∴M,D1(0,2,4),C(2,2,0).∴N点坐标为(1,2,2).8.解:把图中的钠原子分成下、中、上三层来写它们所在位置的坐标.下层的原子全部在xOy平面上,它们所在位置的竖坐标全是0,所以这五个钠原子所在位3置的坐标分别是(0,0,0),(1,0,0),(1,1,0),(0,1,0),;中层的原子所在的平面平行xOy平面,与z轴交点的竖坐标为,所以,这四个钠原子所在位置的坐标分别是,,,;上层的原子所在的平面平行于xOy平面,与z轴交点的竖坐标为1,所以,这五个钠原子所在位置的坐标分别是(0,0,1),(1,0,1),(1,1,1),(0,1,1),.9.解:以OA,OC,OO1所在直线为x轴、y轴、z轴建立空间直角坐标系,由于D在xOy平面内,故D的z坐标(竖坐标)为0,在平面直角坐标系xOy中,如图.∵OA=2,AB=3,∴A(2,0),C(0,3),设D(x0,y0).由OD⊥AC,得,①又D在AC上,∴有.②4由①②解得∴空间坐标系中,D的坐标为.5