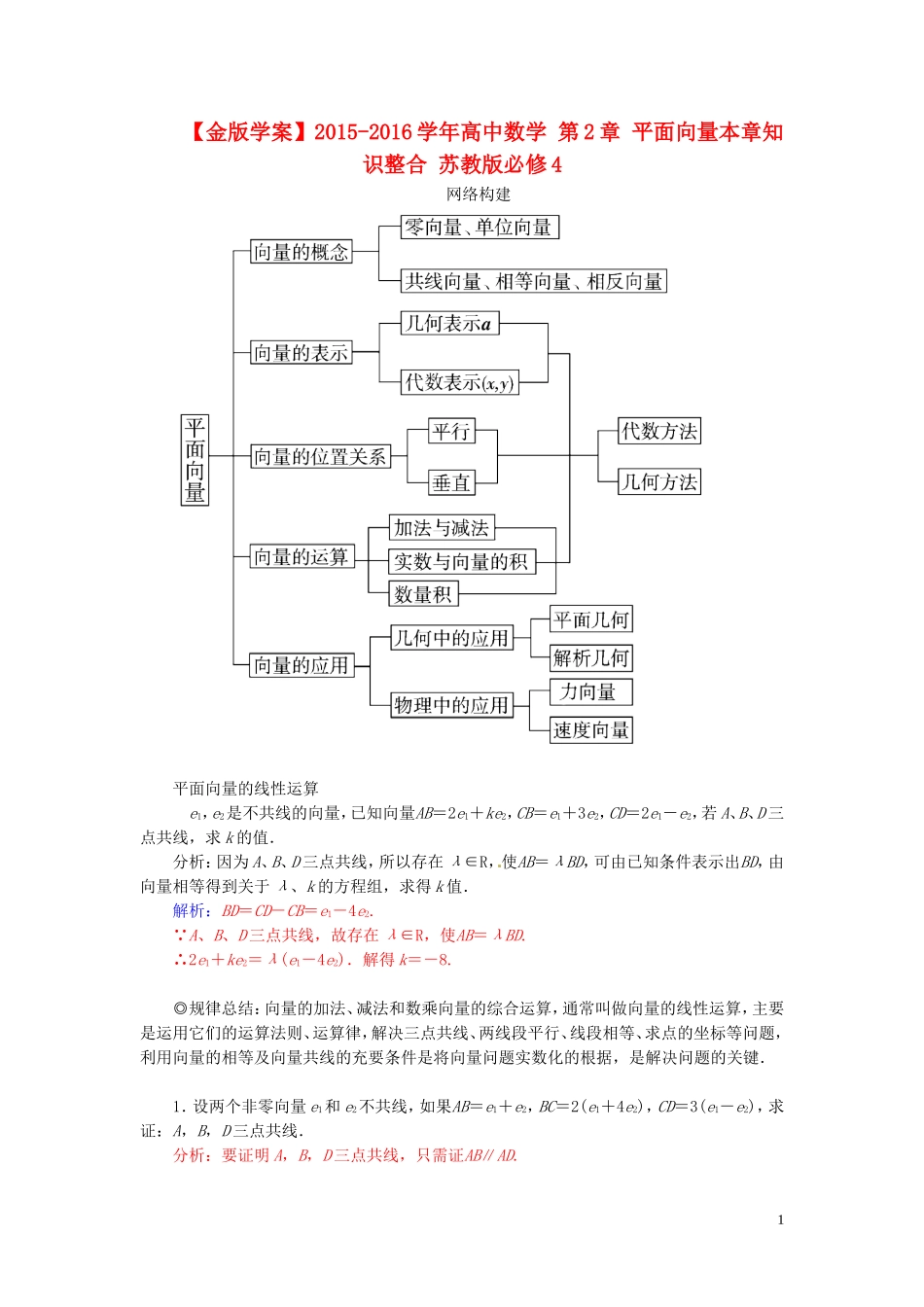
【金版学案】2015-2016学年高中数学第2章平面向量本章知识整合苏教版必修4网络构建平面向量的线性运算e1,e2是不共线的向量,已知向量AB=2e1+ke2,CB=e1+3e2,CD=2e1-e2,若A、B、D三点共线,求k的值.分析:因为A、B、D三点共线,所以存在λ∈R,使AB=λBD,可由已知条件表示出BD,由向量相等得到关于λ、k的方程组,求得k值.解析:BD=CD-CB=e1-4e2. A、B、D三点共线,故存在λ∈R,使AB=λBD.∴2e1+ke2=λ(e1-4e2).解得k=-8.◎规律总结:向量的加法、减法和数乘向量的综合运算,通常叫做向量的线性运算,主要是运用它们的运算法则、运算律,解决三点共线、两线段平行、线段相等、求点的坐标等问题,利用向量的相等及向量共线的充要条件是将向量问题实数化的根据,是解决问题的关键.1.设两个非零向量e1和e2不共线,如果AB=e1+e2,BC=2(e1+4e2),CD=3(e1-e2),求证:A,B,D三点共线.分析:要证明A,B,D三点共线,只需证AB∥AD.1证明: AD=AB+BC+CD=(e1+e2)+2(e1+4e2)+3(e1-e2)=6(e1+e2)=6AB,∴AB,AD为共线向量.又AB,AD有公共点A,故A,B,D三点共线.2.如图所示,OM∥AB,点P在由射线OM、线段OB及AB的延长线所围成的阴影区域内(不含边界)运动,且OP=xOA+yOB,则x的取值范围是________________,当x=-时,y的取值范围是________.解析: OP=xOA+yOB,据平面向量基本定理,取OA的相反向量OA′, y可以变化,∴x可以取任意负实数,故x∈(-∞,0).当x=-时,OA′=-OA.过点A′作OB的平行线交OM于点M,过M作OA′的平行线交OB于点E,则OE=OB.同理,过A′作OB的平行线交AB的延长线于点F.再过F作OA的平行线交OB的延长线于点H,则OH=OB,因不包括边界,故y∈.答案:(-∞,0)向量的坐标运算已知点O(0,0),A(1,2),B(4,5)及OP=OA+tAB.(1)当t为何值时,P在x轴上?在y轴上?在第二象限?(2)四边形OABP能否成为平行四边形?若能,求出相应的t值;若不能,请说明理由.分析:(1)将OP的坐标用t表示出来,然后讨论OP的横、纵坐标.(2)若能成为平行四边形,则有OA=PB,解出t的值;若t无解,则不能构成平行四边形.解析:(1) OA=(1,2),AB=(3,3),∴OP=OA+tAB=(1+3t,2+3t).若点P在x轴上,则2+3t=0,t=-;若点P在y轴上,则1+3t=0,t=-;若点P在第二象限,则解得-<t<-.(2) OA=(1,2),PB=PO+OB=(3-3t,3-3t).若四边形OABP为平行四边形,则OA=PB.又无解,故四边形OABP不能成为平行四边形.◎规律总结:向量的坐标表示实际上就是向量的代数表示,引入向量的坐标表示,向量的运算完全化为代数运算,达到了数与形的统一,通过向量的坐标运算主要解决求向量的坐标、向量的模,判断共线、平行等问题.3.已知A(-2,4),B(3,-1),C(-3,-4),且CM=3CA,CN=2CB,求向量MN的坐标.分析:要求MN的坐标只要求出M、N点的坐标即可.为此须设出M、N的坐标,然后用已知条件求出.2解析:设M点坐标为(x,y),依题意有CA=(1,8),CB=(6,3),CM=(x+3,y+4). CM=3CA,∴(x+3,y+4)=3(1,8).解得x=0,y=20,即M的坐标为(0,20),同理可得N的坐标为(9,2),∴MN=(9,-18).4.在△ABC中,AB=AC,D为AB的中点,E为△ACD的重心,F为△ABC的外心,证明EF⊥CD.证明:建立如图所示的平面直角坐标系.设A(0,b),B(-a,0),C(a,0),则D,CD=,易知△ABC的外心F在y轴上.可设F(0,y),由|AF|=|CF|,可得(y-b)2=a2+y2,所以y=,即F.又由重心坐标公式得E,则EF=,所以CD·EF=×+×=0.所以CD⊥EF,即EF⊥CD.平面向量的数量积设0<|a|≤2,且函数f(x)=cos2x-|a|sinx-|b|的最大值为0,最小值为-4,且a与b的夹角为45°,求|a+b|.分析:要求|a+b|需知道|a|、|b|,故可利用函数的最值确立|a|、|b|的值.解析:f(x)=1-sin2x-|a|sinx-|b|=-+-|b|+1. 0<|a|≤2,∴当sinx=-时,|a|2-|b|+1=0;当sinx=1时,-|a|-|b|=-4.由⇒∴|a+b|2=8+4,即|a+b|=2.◎规律总结:平面向量的数量积是向量的核心内容,通过向量的数量积考查向量的平行、垂直等关系,利用数量积可以计...