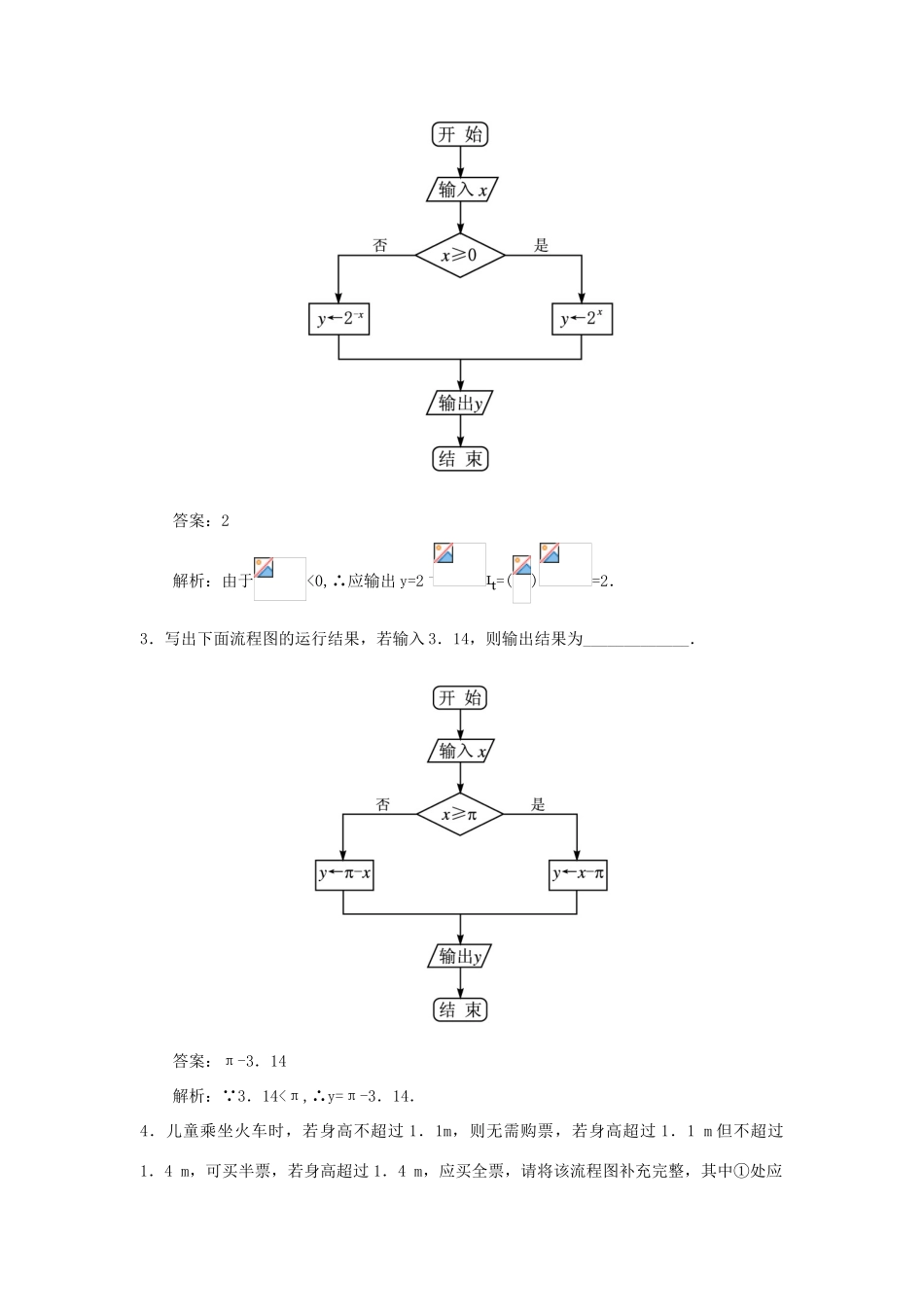
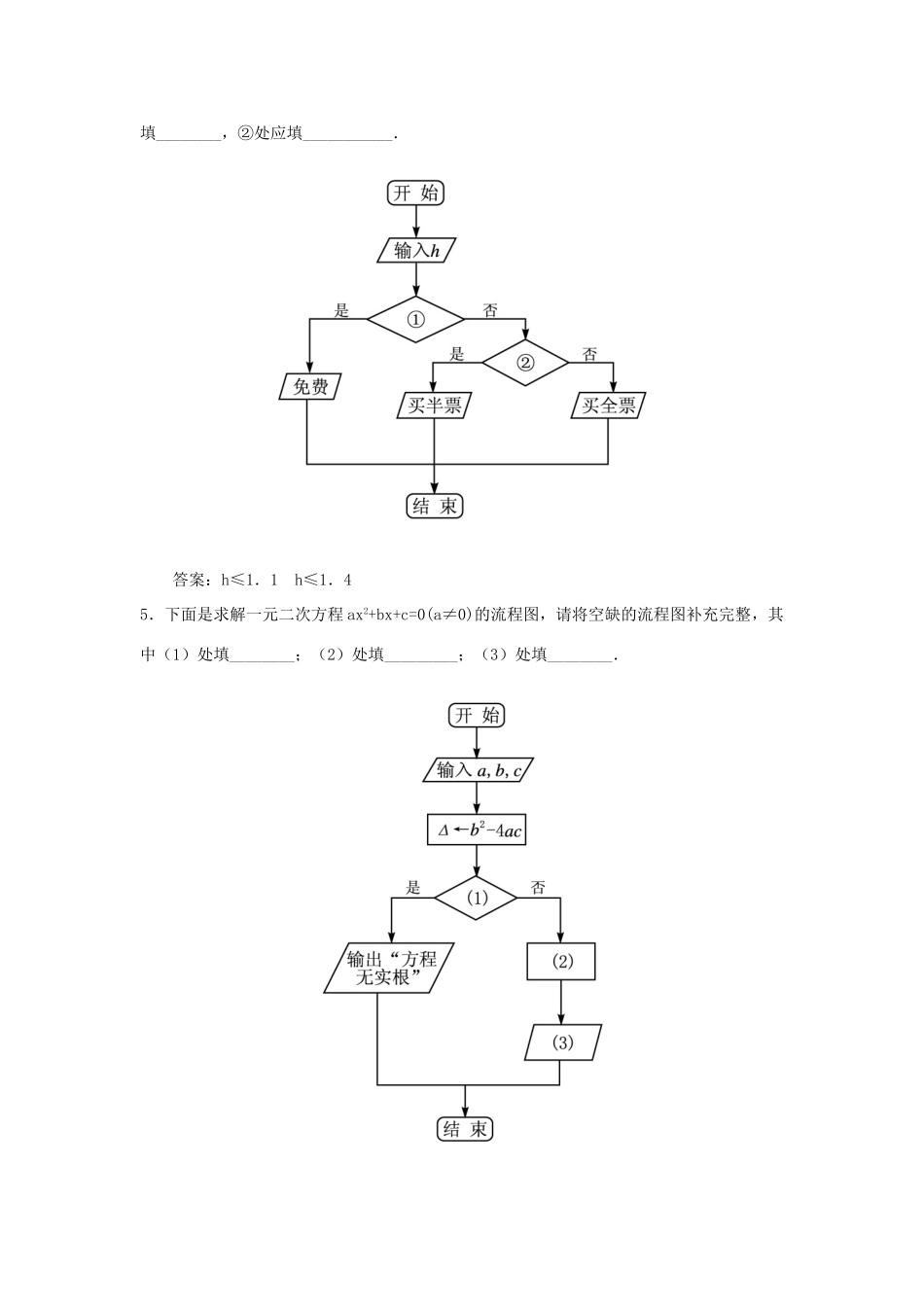
1.2.2选择结构自我检测基础达标1.已知函数y=以下流程图表示的是给定x的值,求其相应函数值的算法,请将该流程图补充完整,其中①处应填___________,②处应填_______________.答案:x≥0y←x+π2.已知函数y=2|x|,如图所示是表示给定x的值,求其相应函数值的算法,若输入,则输出结果为__________.答案:2解析:由于<0,∴应输出y=2-=()=2.3.写出下面流程图的运行结果,若输入3.14,则输出结果为_____________.答案:π-3.14解析:∵3.14<π,∴y=π-3.14.4.儿童乘坐火车时,若身高不超过1.1m,则无需购票,若身高超过1.1m但不超过1.4m,可买半票,若身高超过1.4m,应买全票,请将该流程图补充完整,其中①处应填________,②处应填___________.答案:h≤1.1h≤1.45.下面是求解一元二次方程ax2+bx+c=0(a≠0)的流程图,请将空缺的流程图补充完整,其中(1)处填________;(2)处填_________;(3)处填________.答案:(1)Δ<0(2)x1=x2=(3)输出x1、x26.下面的流程图表示了一个什么样的算法?解析:第一步:是输入a,b,c三个数;第二步:是判断a与b,a与c的大小,如果a同时大于b,c,则输出a,否则执行第三步;第三步:判断b与c的大小,因为a已小于b或c,则只需比较b与c的大小就能看出a,b,c中谁是最大的了,如果b>c,则输出b,否则输出C.通过上面的分析,流程图表示一个什么样的问题已经非常清楚了.给任意三个数a,b,c,输出最大的一个数.7.写出解方程ax+b=0(a,b为常数)的算法,并画出流程图.解析:第一步:判断a是否为零?若a≠0,执行第二步,若a=0,执行第四步;第二步:计算;第三步:输出“方程的解为”;第四步:判断b是否为零?若b=0,输出“有无数个解”的信息,若b≠0,输出“方程无解”的信息.流程图如图所示:8.某居民区的物业部门每月收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元,设计一个算法,根据输入的人数,计算应收取的卫生费,并画出流程图.解:算法步骤:第一步:输入人数x,设收取的卫生费为m元.第二步:判断x与3的大小.若x>3,则费用为m=5+(x-3)×1.2;若x≤3,则费用为m=5.第三步:输出m.流程图如图所示:9.观察所给的流程图,说出它所表示的函数.解析:由流程图可以看出这是一复合选择结构,可根据判断条件确定算法流向,因此所表示函数为一分段函数.更上一层1.设n为正整数,它被3除余数为r,当r=0时,输出2n;当r=1时,输出3;当r=2时,输出5,画出该算法的流程图.解:流程图如图:注意:由于正整数n被3除,其余数有3个可能的情况:r=0,r=1,r=2.当r≠0且r≠1时r一定为2,故本题不需要r是否等于2这一判断框.2.试写出解不等式ax+b>0(a≠0)的流程图.解:流程图如图:3.火车站对乘客退票收取一定的费用,具体办法是:按票价每10元(不足10元按10元计算)核收2元;2元以下的票不退.试写出票价为x元的车票退掉后,返还的金额y元的算法的流程图.解: