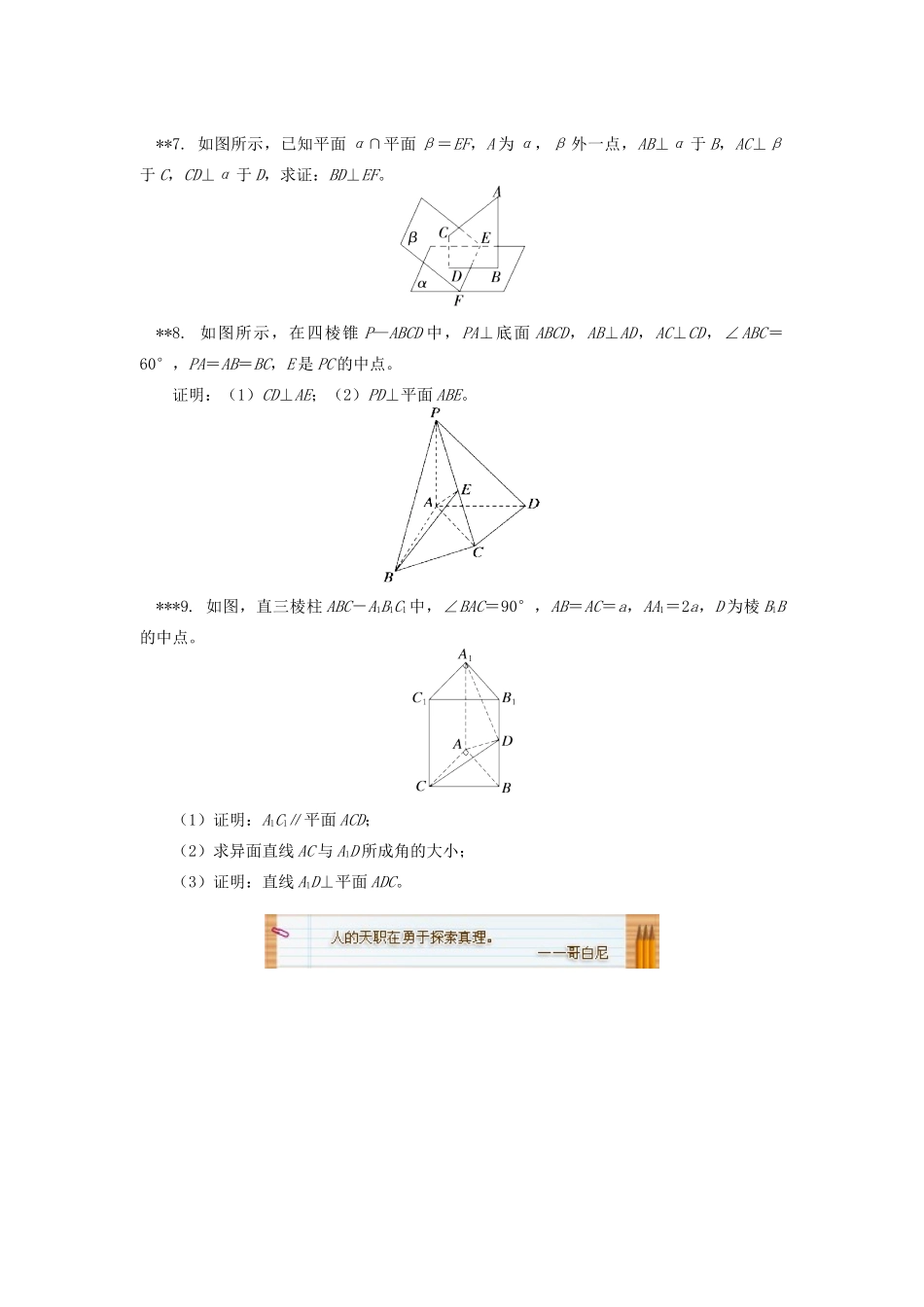
线面垂直的综合运用(答题时间:40分钟)*1.下列条件中,能判定直线l⊥平面α的有________。①l与平面α内的两条直线垂直;②l与平面α内的无数条直线垂直;③l与平面α内的某一条直线垂直;④l与平面α内的任意一条直线垂直。**2.在正方体ABCD-A1B1C1D1中,已知AB=1,则点C到平面B1BDD1的距离为________。**3.(无锡检测)△ABC中,∠ABC=90°,PA⊥平面ABC,则图中直角三角形的个数为________。*4.如图,∠BAC=90°,PC⊥平面ABC,则在△ABC,△PAC的边所在的直线中:与PC垂直的直线有______________;与AP垂直的直线有________。**5.如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的正投影,给出下列结论:①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC其中正确结论的序号是________。**6.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面是边长为2的菱形,且∠ABC=45°,PA=AB,则直线AP与平面PBC所成角的正切值为________。**7.如图所示,已知平面α∩平面β=EF,A为α,β外一点,AB⊥α于B,AC⊥β于C,CD⊥α于D,求证:BD⊥EF。**8.如图所示,在四棱锥P—ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点。证明:(1)CD⊥AE;(2)PD⊥平面ABE。***9.如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D为棱B1B的中点。(1)证明:A1C1∥平面ACD;(2)求异面直线AC与A1D所成角的大小;(3)证明:直线A1D⊥平面ADC。1.④解析:由线面垂直的定义及判定定理可知④正确。2.解析:连接AC,则AC⊥BD,又BB1⊥AC,故AC⊥平面B1BDD1,所以点C到平面B1BDD1的距离为AC=。3.4解析:∵PA⊥平面ABC,∴PA⊥AB,PA⊥AC,PA⊥BC,又BC⊥AB,AB∩PA=A,∴BC⊥平面PAB,∴BC⊥PB,综上可知△PAB,△PAC,△ABC,△PBC均为直角三角形。4.AB,BC,ACAB解析:∵PC⊥平面ABC,∴PC垂直于直线AB,BC,AC;∵AB⊥AC,AB⊥PC,∴AB⊥平面PAC,∴AB⊥PC.与AP垂直的直线是AB。5.①②③解析:由题意知PA⊥平面ABC,∴PA⊥BC,又AC⊥BC,PA∩AC=A,∴BC⊥平面PAC,∴BC⊥AF.∵AF⊥PC,BC∩PC=C,∴AF⊥平面PBC,∴AF⊥PB,AF⊥BC,又AE⊥PB,AE∩AF=A,∴PB⊥平面AEF,∴EF⊥PB,故①②③正确。6.解析:作AE⊥BC于点E,则BC⊥平面PAE,故∠APE为直线AP与平面PBC所成的角,AE=ABsin45°=,∴tan∠APE==。7.证明:∵AB⊥α,CD⊥α,∴AB∥CD.∴A,B,C,D四点共面,∵AB⊥α,AC⊥β,α∩β=EF,∴AB⊥EF,AC⊥EF,又∵AB∩AC=A,∴EF⊥平面ABDC,∴BD⊥EF。8.证明:(1)在四棱锥P—ABCD中,∵PA⊥底面ABCD,CD⊂平面ABCD,∴PA⊥CD.∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC,而AE⊂平面PAC,∴CD⊥AE;(2)由PA=AB=BC,∠ABC=60°,可得AC=PA,∵E是PC的中点,∴AE⊥PC,由(1),知AE⊥CD,且PC∩CD=C,∴AE⊥平面PCD,而PD⊂平面PCD,∴AE⊥PD,∵PA⊥底面ABCD,∴PA⊥AB,又∵AB⊥AD且PA∩AD=A,∴AB⊥平面PAD,而PD⊂平面PAD,∴AB⊥PD,又∵AB∩AE=A,∴PD⊥平面ABE。9.(1)证明:在直三棱柱ABC-A1B1C1中,AC∥A1C1,又A1C1⊄平面ACD,AC⊂平面ACD,∴A1C1∥平面ACD;(2)解:在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∴A1A⊥AC,又∠BAC=90°,∴AC⊥AB.又AA1∩AB=A,∴AC⊥平面A1ABB1,又A1D⊂平面A1ABB1,∴AC⊥A1D,∴异面直线AC与A1D所成的角为90°,(3)证明:∵△A1B1D和△ABD都为等腰直角三角形,∴∠A1DB1=∠ADB=45°,∴∠A1DA=90°,即A1D⊥AD,由(2)知A1D⊥AC,且AD∩AC=A,∴A1D⊥平面ADC。