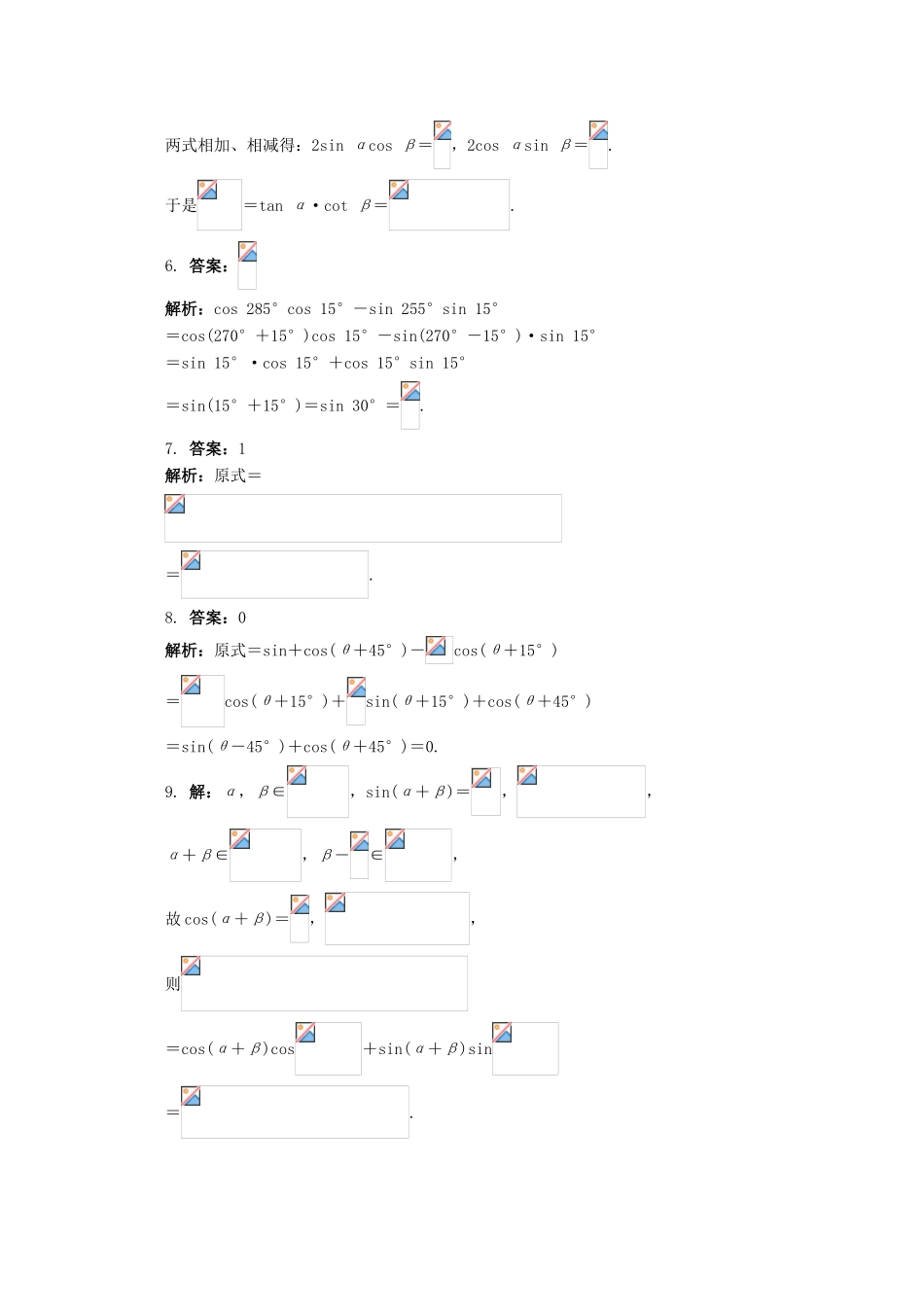
高中数学5.1.1两角和与差的正弦和余弦第二课时同步练习湘教版必修21.在△ABC中,若sin(B+C)=2sinBcosC,那么这个三角形一定是()A.锐角三角形B.钝角三角形C.直角三角形D.等腰三角形2.若cosα=,α是第三象限角,则()A.B.C.D.3.对任意α,β∈,sin(α+β)与sinα+sinβ的大小关系是()A.sin(α+β)>sinα+sinβB.sin(α+β)<sinα+sinβC.sin(α+β)=sinα+sinβD.视α,β的具体值而定4.已知0<α≤<β≤π,又sinα=,cos(α+β)=,则sinβ=()A.0B.0或C.D.0或5.已知sin(α+β)=,sin(α-β)=,则的值是()A.B.C.D.6.cos285°cos15°-sin255°sin15°=________.7.的值为__________.8.式子sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值等于__________.9.已知α,β∈,sin(α+β)=,,求的值.10.已知α,β均为锐角,且cosα=,sinβ=,求α-β的值.参考答案1.答案:D解析:∵sin(B+C)=2sinBcosC,∴sinBcosC+cosBsinC=2sinBcosC,移项整理得:sinBcosC-cosBsinC=0,即sin(B-C)=0.又0<B<π,0<C<π,∴-π<B-C<π,∴B-C=0,∴B=C.∴△ABC为等腰三角形.2.答案:A解析:由于α是第三象限角且cosα=,∴sinα=.∴=sinαcos+cosαsin=.3.答案:B解析:∵sin(α+β)=sinαcosβ+cosαsinβ,由于α,β∈,∴cosβ∈(0,1),cosα∈(0,1).∴sin(α+β)<sinα+sinβ.4.答案:B解析:∵α∈,sinα=,∴cosα=.∵0<α≤<β≤π,cos(α+β)=,∴α+β∈,sin(α+β)=或sin(α+β)=.∴sinβ=sin=sin(α+β)cosα-cos(α+β)sinα.代入求值得sinβ=0或sinβ=,故选B.5.答案:C解析:由已知得sinαcosβ+cosαsinβ=,sinαcosβ-cosαsinβ=,两式相加、相减得:2sinαcosβ=,2cosαsinβ=.于是=tanα·cotβ=.6.答案:解析:cos285°cos15°-sin255°sin15°=cos(270°+15°)cos15°-sin(270°-15°)·sin15°=sin15°·cos15°+cos15°sin15°=sin(15°+15°)=sin30°=.7.答案:1解析:原式==.8.答案:0解析:原式=sin+cos(θ+45°)-cos(θ+15°)=cos(θ+15°)+sin(θ+15°)+cos(θ+45°)=sin(θ-45°)+cos(θ+45°)=0.9.解:α,β∈,sin(α+β)=,,α+β∈,β-∈,故cos(α+β)=,,则=cos(α+β)cos+sin(α+β)sin=.10.解:已知α,β均为锐角,且cosα=,则.又∵sinβ=,∴.∴sin(α-β)=sinαcosβ-cosαsinβ=.∵sinα<sinβ,∴0<α<β<.∴<α-β<0,∴α-β=.