高中数学 3.2.3 诱导公式第一课时诱导公式（一）同步练习 湘教版必修2-湘教版高一必修2数学试题VIP专享VIP免费

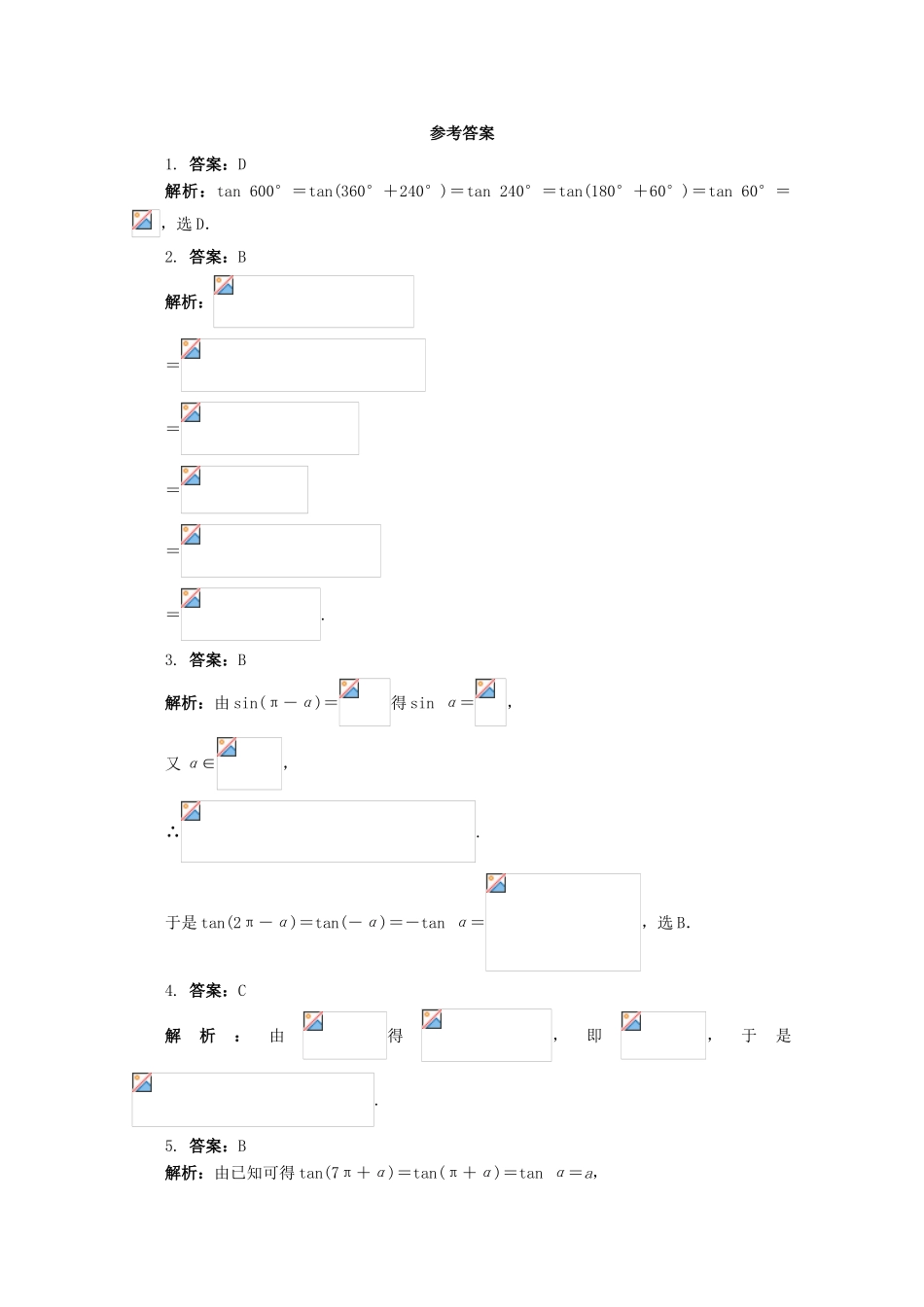
高中数学3.2.3诱导公式第一课时诱导公式（一）同步练习湘教版必修21．tan600°的值是()A．B．C．D．2．＝()A．B．C．0D．23．已知sin(π－α)＝，且α∈，则tan(2π－α)的值为()A．B．C．D．4．已知，则的值等于()A．mB．－mC．D．5．若tan(7π＋α)＝a，则的值为()A．B．C．－1D．16．求值：__________.7．cos1°＋cos2°＋cos3°＋…＋cos180°＝__________.8．若cos(－50°)＝k，则tan130°＝__________.9．已知tan(π＋α)＝，求下列各式的值．(1)；(2)sin(α－7π)·cos(α＋5π)．10．是否存在角α，β，α∈，β∈(0，π)，使等式sin(3π－α)＝，＝cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，请说明理由．参考答案1.答案：D解析：tan600°＝tan(360°＋240°)＝tan240°＝tan(180°＋60°)＝tan60°＝，选D．2.答案：B解析：＝＝＝＝＝.3.答案：B解析：由sin(π－α)＝得sinα＝，又α∈，∴.于是tan(2π－α)＝tan(－α)＝－tanα＝，选B．4.答案：C解析：由得，即，于是.5.答案：B解析：由已知可得tan(7π＋α)＝tan(π＋α)＝tanα＝a，因此原式＝＝＝.选B．6.答案：解析：＝＝.7.答案：－1解析：原式＝cos1°＋cos2°＋cos3°＋…＋cos89°＋cos90°＋cos(180°－89°)＋…＋cos(180°－2°)＋cos(180°－1°)＋cos180°＝(cos1°－cos1°)＋(cos2°－cos2°)＋…＋(cos89°－cos89°)＋cos90°＋cos180°＝＋0＋(－1)＝－1.8.答案：解析：由已知得cos50°＝k，所以sin50°＝.于是tan130°＝－tan50°＝.9.解：tan(π＋α)＝tanα＝，(1)＝.(2)原式＝－sinα·(－cosα)＝sinα·cosα＝＝.10.解：利用诱导公式可将已知条件化为两式平方相加得sin2α＋3cos2α＝2，即sin2α＝，所以sinα＝.因为α∈，所以或.当时，由①式可得sinβ＝，由②式可得cosβ＝，又β∈(0，π)，所以.当时，由①式可得，这与β∈(0，π)矛盾．从而只存在，使得两个等式同时成立．