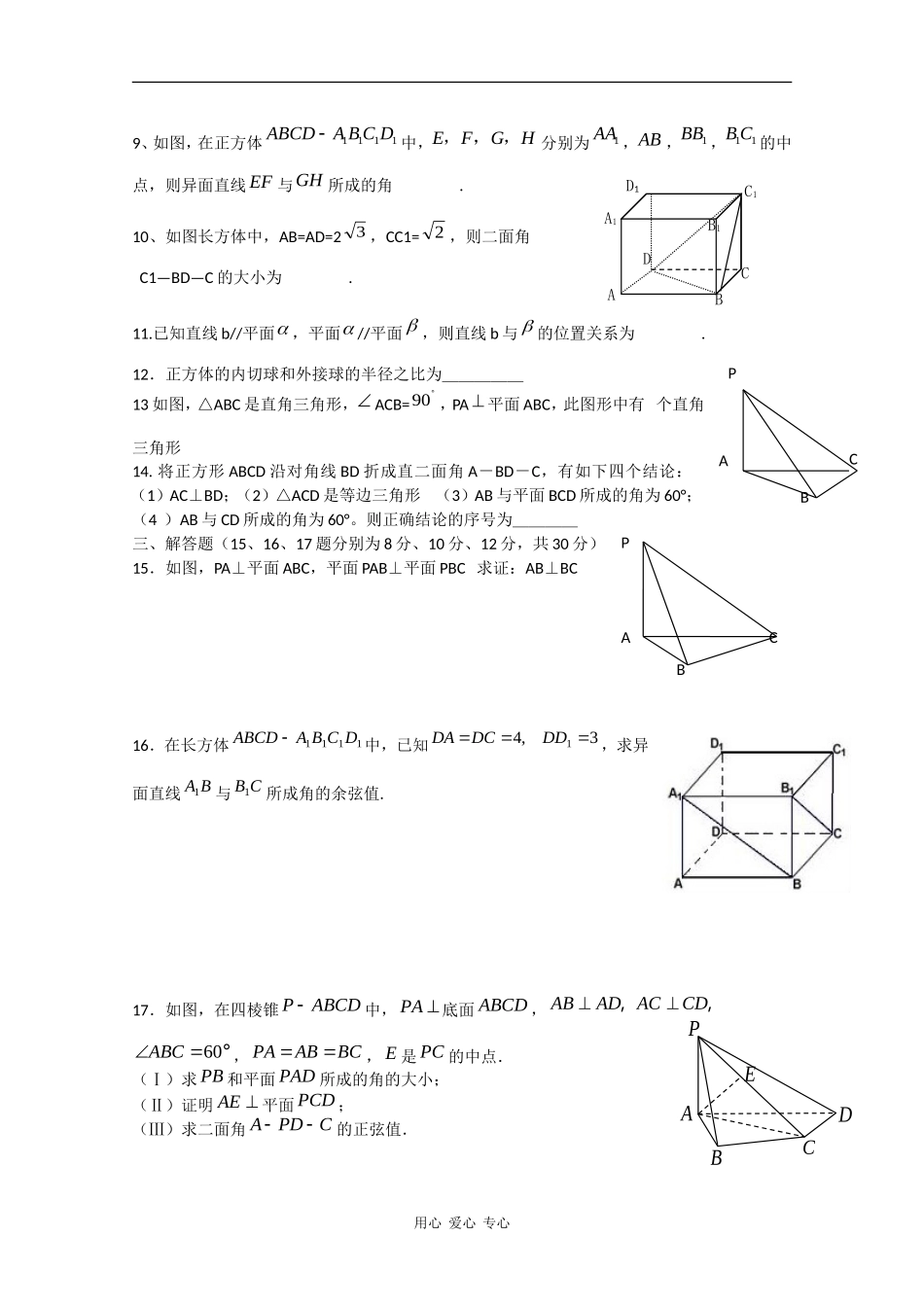
立体几何练习一、选择题(本大题共10小题,每小题5分,共50分)1、已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.则该几何体的体积为()(A)48(B)64(C)96(D)1922.棱长都是1的三棱锥的表面积为()A.3B.23C.33D.433.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是()A.25B.50C.125D.都不对4、在空间四边形ABCD中,AB、BC、CD、DA上分别取E、F、G、H四点,如果GH、EF交于一点P,则()A.P一定在直线BD上B.P一定在直线AC上C.P在直线AC或BD上D.P既不在直线BD上,也不在AC上5、若l、m、n是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是()A.若//,,ln,则//lnB.若,l,则lC.若,//ll,则D.若,lnmn,则//lm6、已知两个平面垂直,下列命题①一个平面内的已知直线必垂直于另一个平面的任意一条直线;②一个平面内的已知直线必垂直于另一个平面的无数条直线;③一个平面内的任一条直线必垂直于另一个平面;④过一个平面内任意一点作交线的垂线,则垂线必垂直于另一个平面.其中正确的个数是()A.3B.2C.1D.07.平面与平面平行的条件可以是()A.内有无穷多条直线与平行;B.直线a//,a//C.直线a,直线b,且a//,b//D.内的任何直线都与平行8、如图,一个封闭的立方体,它的六个表面各标有A,B,C,D,E,F这六个字母之一,现放置成如图的三种不同的位置,则字母A,B,C对面的字母分别为()A)D,E,FB)F,D,EC)E,F,DD)E,D,F二、填空题(本大题共4小题,每小题5分,共20分)用心爱心专心CBAADCEBCAFDBCGE1BH1C1D1A9、如图,在正方体1111ABCDABCD中,EFGH,,,分别为1AA,AB,1BB,11BC的中点,则异面直线EF与GH所成的角.10、如图长方体中,AB=AD=23,CC1=2,则二面角C1—BD—C的大小为.11.已知直线b//平面,平面//平面,则直线b与的位置关系为.12.正方体的内切球和外接球的半径之比为_____13如图,△ABC是直角三角形,ACB=90,PA平面ABC,此图形中有个直角三角形14.将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:(1)AC⊥BD;(2)△ACD是等边三角形(3)AB与平面BCD所成的角为60°;(4)AB与CD所成的角为60°。则正确结论的序号为____三、解答题(15、16、17题分别为8分、10分、12分,共30分)15.如图,PA⊥平面ABC,平面PAB⊥平面PBC求证:AB⊥BC16.在长方体1111DCBAABCD中,已知3,41DDDCDA,求异面直线BA1与CB1所成角的余弦值.17.如图,在四棱锥PABCD中,PA底面ABCD,ABADACCD,,60ABC°,PAABBC,E是PC的中点.(Ⅰ)求PB和平面PAD所成的角的大小;(Ⅱ)证明AE平面PCD;(Ⅲ)求二面角APDC的正弦值.用心爱心专心ABCPPABCABCDPEABCDA1B1C1D11、B2.A3.B长方体对角线是球直径,22225234552,252,,4502lRRSR4.B5、C6、C7、D8、D9、60°10、30°11、平行或在平面内;12、正方体的棱长是内切球的直径,正方体的对角线是外接球的直径,设棱长是a32,32,1322aaarrarrrr内切球内切球外接球外接球内切球外接球,,::13、414、(1)(2)(4)15、证明:过A作AD⊥PB于D,由平面PAB⊥平面PBC,得AD⊥平面PBC,故AD⊥BC,又BC⊥PA,故BC⊥平面PAB,所以BC⊥AB16、连接DA1,DBACBDA111,//为异面直线BA1与CB1所成的角.连接BD,在△DBA1中,24,511BDDABA,则DABABDDABADBA112212112cos259552322525.17、(Ⅰ)解:在四棱锥PABCD中,因PA底面ABCD,AB平面ABCD,故PAAB.又ABAD,PAADA,从而AB平面PAD.故PB在平面PAD内的射影为PA,从而APB∠为PB和平面PAD所成的角.在RtPAB△中,ABPA,故45APB∠.所以PB和平面PAD所成的角的大小为45.(Ⅱ)证明:在四棱锥PABCD中,因PA底面ABCD,CD平面ABCD,故CDPA.由条件CDAC,PAACA,CD面PAC.又AE...