高一数学平面向量的数量积及应用同步练习北师大版VIP免费

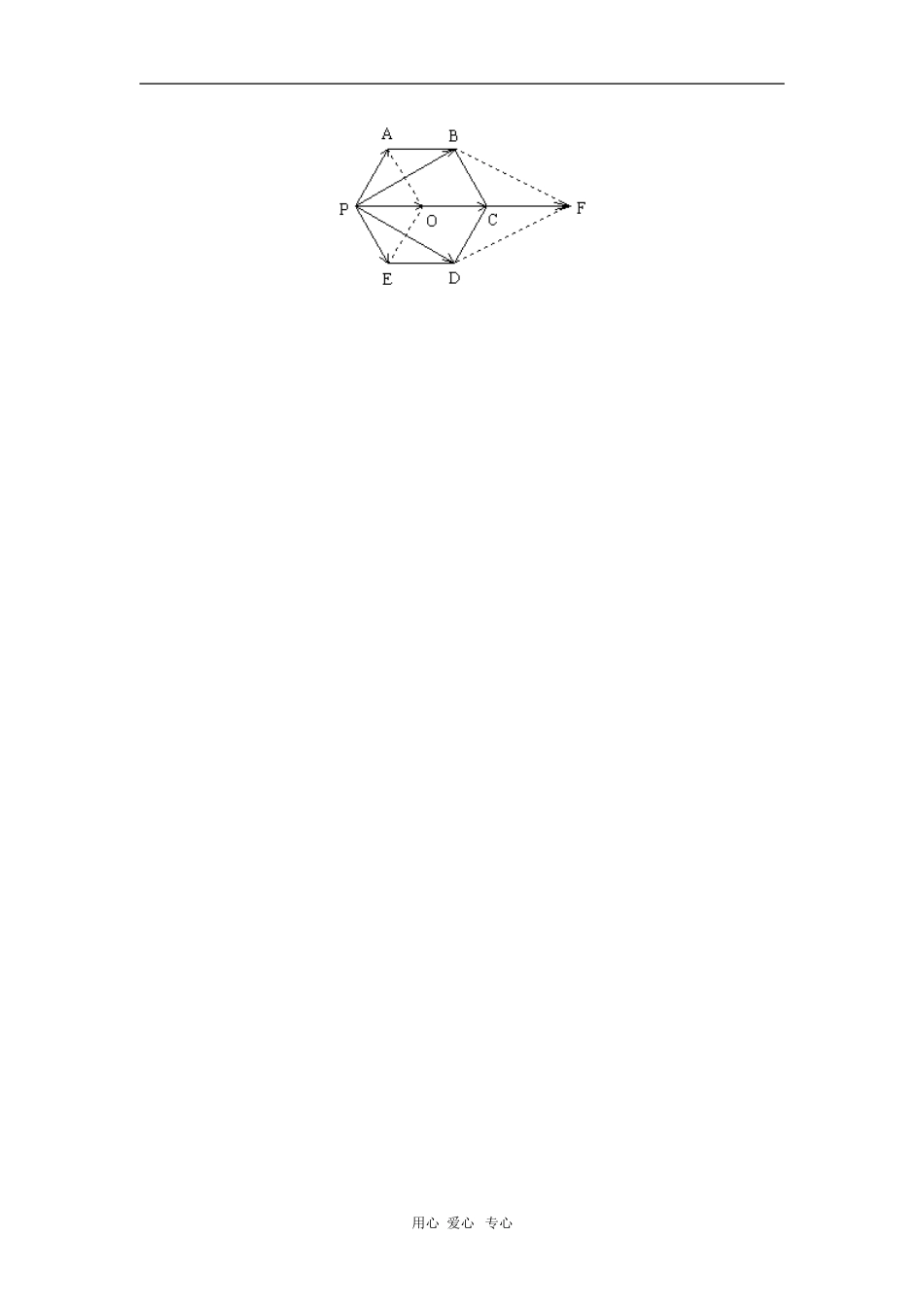
高一数学平面向量的数量积及应用同步练习北师大版（答题时间：60分钟）一、选择题1、已知平面向量=（1，－3），=（4，－2），ab与垂直，则是A.－1B.1C.－2D.22、在ABC中，AB=3，AC=2，BC=10，则ABAC�A.23B.32C.32D.233、已知四边形ABCD的三个顶点(02)A，，(12)B，，(31)C，，且2BCAD�，则顶点D的坐标为A.722，B.122，C.(32)，D.(13)，4、若向量与b不共线，，且，则向量a与c的夹角为A.0B.π6C.π3D.π25、设(43)，a，a在b上的投影为522，b在x轴上的投影为2，且||14≤b，则b为A.(214)，B.227，C.227，D.(28)，6、设，ab是非零向量，若函数的图象是一条直线，则必有A.⊥abB.∥abC.||||abD.||||ab二、填空题7、已知向量a与b的夹角为120，且4ab，那么的值为.8、，的夹角为120，1a，3b，则5ab.三、解答题9、已知△ABC顶点的直角坐标分别为)0,()0,0()4,3(cCBA、、.（1）若5c，求sin∠A的值；（2）若∠A是钝角，求c的取值范围.*10、在ABC△中，角ABC，，的对边分别为tan37abcC，，，.（1）求cosC；（2）若52CBCA�，且9ab，求c.11、已知向量m=（sinA，cosA），n=，m·n＝1，且A为锐角.（Ⅰ）求角A的大小；（Ⅱ）求函数的值域.*12、如图所示，正六边形PABCDE的边长为b，有五个力PDPCPBPA、、、、PE作用于同一点P，求五个力的合力。用心爱心专心用心爱心专心【试题答案】一、选择题1.A2.D3.A4.D5.D6.A二、填空题7.－88.7三、解答题9、解：（1）(3,4)AB�，(3,4)ACc�当c=5时，(2,4)AC�6161coscos,5255AACAB�进而225sin1cos5AA（2）若A为钝角，则AB·AC=－3（c－3）+（－4）2<0解得c>325显然此时有AB和AC不共线，故当A为钝角时，c的取值范围为[325，+]10、解：（1）sintan3737cosCCC，又22sincos1CC解得1cos8C.tan0C，C是锐角.1cos8C.（2），5cos2abC，20ab.又9ab22281aabb.2241ab.2222cos36cababC.6c.11、解：（Ⅰ）由题意得m·n由A为锐角得（Ⅱ）由（Ⅰ）知所以因为x∈R，所以，因此，当时，f（x）有最大值.当sinx=－1时，f（x）有最小值－3，所以所求函数f（x）的值域是.12、解：所求五个力的合力为PEPDPCPBPA，如图所示，以PA、PE为边作平行四边形PAOE，则PEPAPO，由正六边形的性质可知b|PA||PO|，且O点在PC上，用心爱心专心以PB、PD为边作平行四边形PBFD，则PDPBPF，由正六边形的性质可知b3|PF|，且F点在PC的延长线上。由正六边形的性质还可求得b2|PC|故由向量的加法可知所求五个力的合力的大小为b6b3b2b，方向与PC的方向相同。用心爱心专心