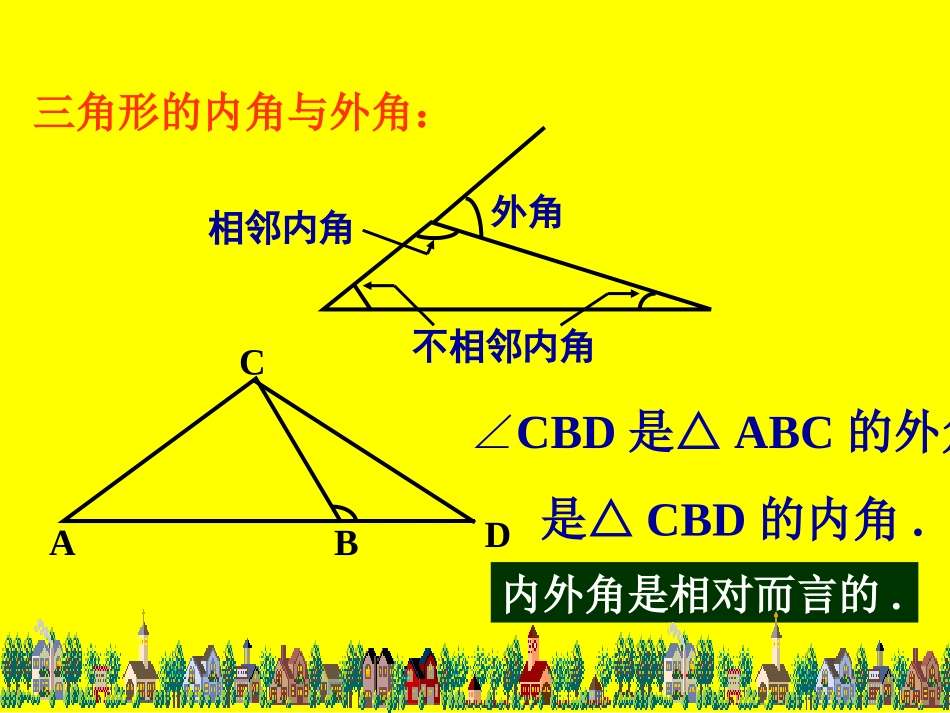
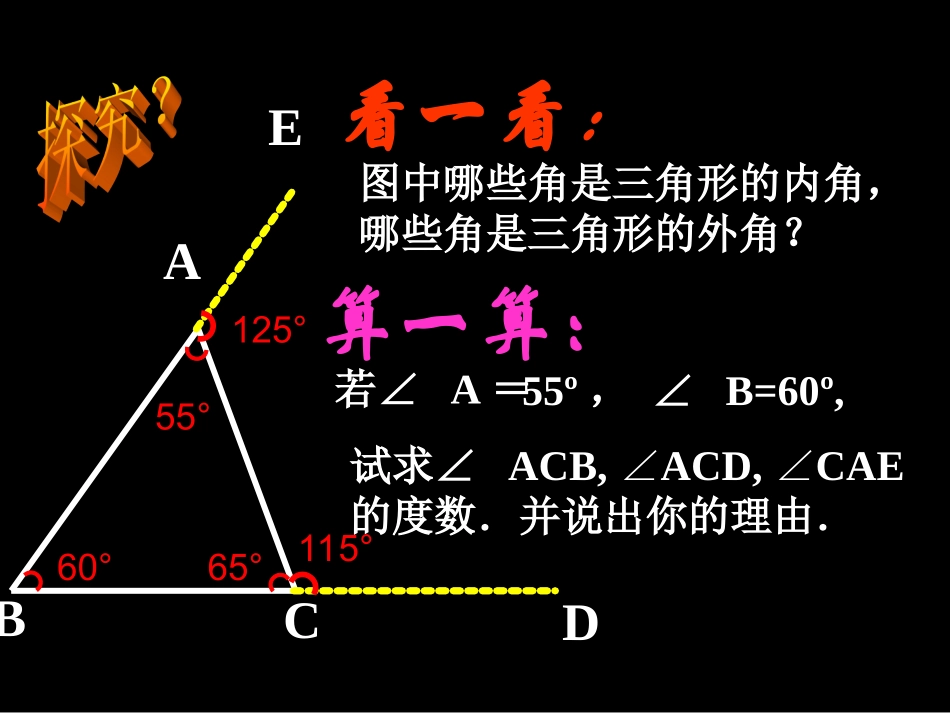
内课题:三角形的外角和三角形的内角与外角:CABD内外角是相对而言的.外角相邻内角不相邻内角∠CBD是△ABC的外角.是△CBD的内角.ABCDE看一看:算一算:若∠A=55º,∠B=60º,试求∠ACB,ACD,CAE∠∠的度数.并说出你的理由.图中哪些角是三角形的内角,哪些角是三角形的外角?⌒⌒⌒⌒⌒115°60°65°55°125°内角与外角有什么关系?(1)相邻:CABD发现:.互为邻补角与CBDABC即:∠CBD(外角)+∠ABC(相邻内角)=180°演示CABD(2)不相邻:?因为180ABCCBD180ABCCA所以∠CBD=A+C∠∠发现:∠CBD=A+C∠∠CABD利用平行线的性质说明.过点B作BEAC∥①因为BEAC∥所以∠1=A,∠12E又因为∠1+2=CBD∠∠所以∠A+C=CBD∠∠CABDE②过点A作AEBCCABDE③过点C作CEAB三角形的外角性质:1、三角形的一个外角等于与它不相邻的两个内角的和;2、三角形的一个外角大于任何一个与它不相邻的内角。∠2=C∠求下列各图中∠1的度数。30°60°135°120°145°50°1∠1=∠1=∠1=90º85º95º把图中∠1、∠2、∠3按由大到小的顺序排列B321ACDE∠1∠2∠3>>>>∠DAC∠C∠BAD∠B______+____________+______122____32____4ABDC1243快速抢答看谁答的又快又准ABC123方法1方法2三角形的外角和等于360°∠1+∠2+∠3=?从哪些途径探究这个结果议一议ABC123∠2+∠ABC=180°∠3+∠ACB=180°三个式子相加得到∠1+∠2+∠3+∠BAC+∠ABC+∠ACB=540°而∠BAC+∠ABC+∠ACB=180°∠1+∠2+∠3=360°∠1+∠BAC=180°解:解:过解:过AA作作ADAD平行于平行于BBCC∴∴∠∠33==∠∠44BC1234A∴∴∠∠22==∠∠BADBAD∴∴∠∠11++∠∠22++∠∠33==∠∠11++∠∠BADBAD++∠∠4=34=360°60°两直线平行,两直线平行,同位角相等同位角相等D例1∠B=BAD∠,∠ADC=80°,∠BAC=70°.求:⑴∠B的度数;⑵∠C的度数。ABCD如图,D是△ABC的BC边上一点,解:⑴因为∠ADC是△ABD的外角,∠ADC=B+BAD=80°∠∠又∠B=BAD∠所以∠B=80°=40°2180°70°所以⑵在△ABC中,所以∠C=180°-∠B-∠BAC=70°因为∠B+BAC+C=180°∠∠=180°-40°-70°例2如图,一根电线杆立于河水中,两岸各用一根铁丝将其固定,现测得铁丝分别与两岸地面成110°和120°的角.求两铁丝所成的角.A解:因为∠ABC+ABD=180°∠所以∠ABC=70°因为∠ACE是△ABC的外角所以∠ACE=ABC∠+∠BAC=120°-70°=50°答:两铁丝所成的角为50°又因为∠ABD=110°所以∠BAC=ACE∠-∠ABCBDCE110°120°1、如图,已知∠AEC=110°,求∠A+∠B+C+D∠∠的度数。ABCDE练习解:因为∠AEC是△ABE的外角,所以∠AEC=A+B=110°∠∠∠AEC=C+D=110°∠∠所以∠A+B+C+D=220°∠∠∠因为∠AEC是△CDE的外角,所以A2、如图在五角星ABCDE中,求∠A+B+∠C+D+E∠∠∠的度数。BCDEFG所以∠A+D+B+E+C=180°∠∠∠∠所以∠2=B+E.∠∠解:如图所示因为∠1是△BEG的外角,所以∠1=A+D.∠∠因为∠2是△AFG的外角,在△CFG中,∠1+2+C=180°∠∠即∠A+B+C+D+E=180°∠∠∠∠12小结:2、三角形的一个外角等于和它不相邻的两个内角的和;1、三角形的外角与相邻内角互补;3、三角形的一个外角大于任何一个和它不相邻的内角;4、三角形的外角和等于360°.㈠结论:㈡思想与方法:1、割补的思想;2、利用平行性质说明;3、运用三角形内、外角性质及三角形内、外角和计算角度.“行家”看“门道”已知:如右图,在△ABC中,AD平分外角∠EAC,∠B=∠C.求证:AD∥BC.证明: ∠EAC=∠B+∠C(三角形的一个外角等于和它不相邻的两个内角的和),∴AD∥BC(内错角相等,两直线平行).∠B=∠C(已知),∴∠DAC=∠C(等量代换).ACDBE分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”. AD平分∠EAC(已知).21∴∠C=∠EAC(等式性质).21∴∠DAC=∠EAC(角平分线的定义).··例题是运用了定理“内错角相等,两直线平行”得到了证实.一题多解思维灵活ACDBE··∠B=∠C(已知),21∴∠B=∠EAC(等式性质). AD平分∠EAC(已知).21∴∠DAE=∠EAC(角平分线的定义).∴∠DAE=∠B(等量代换).∴AD∥BC(同位角相等,两直线平行).这里是运用了公理“同位角相等,两直...