椭圆的简单几何性质VIP免费

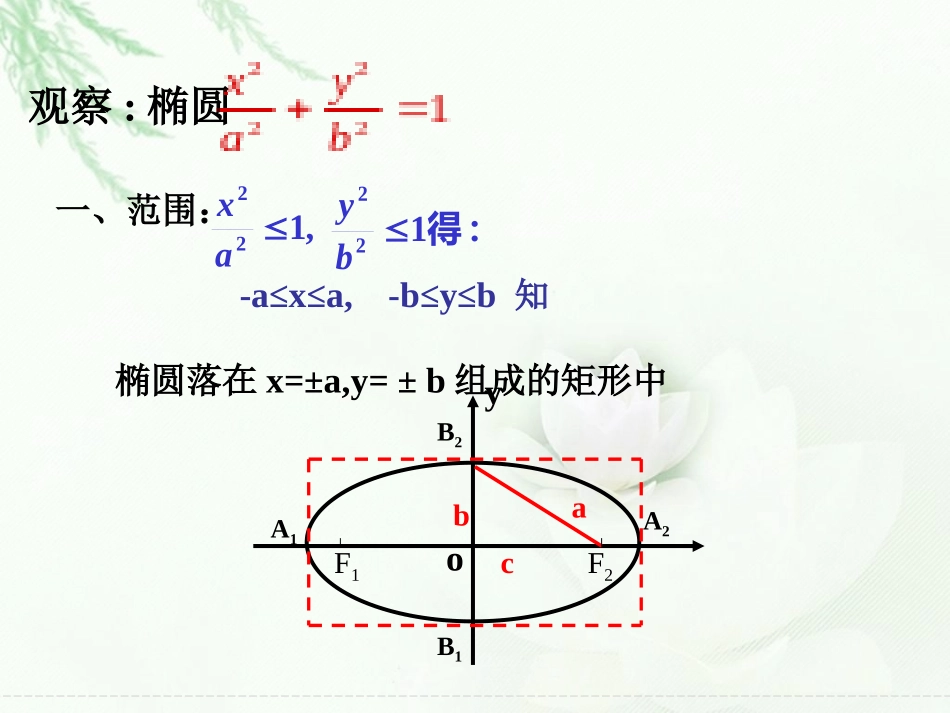
复习：1.椭圆的定义:到两定点F1、F2的距离之和为常数（大于|F1F2|）的动点的轨迹叫做椭圆。2.椭圆的标准方程是：3.椭圆中a,b,c的关系是:a2=b2+c2|)|2(2||||2121FFaaPFPF当焦点在X轴上时当焦点在Y轴上时)0(12222babyax)0(12222babxay-a≤x≤a,-b≤y≤b知椭圆落在x=±a,y=±b组成的矩形中,122ax得：122byoyB2B1A1A2F1F2cab一、范围：观察:椭圆11625.122yx口答下列椭圆的范围。练习44,55yx≤≤≤≤YXOP（x，y）P2（-x，y）P3（-x，-y）P1（x，-y）22221(0)xyabab关于x轴对称关于y轴对称关于原点对称椭圆对称性从方程上看：（1）把x换成-x方程不变，图象关于轴对称；（2）把y换成-y方程不变，图象关于轴对称；（3）把x换成-x，同时把y换成-y方程不变，图象关于成中心对称。)0(12222babyaxyx原点坐标轴是椭圆的对称轴，原点是椭圆的对称中心。中心：椭圆的对称中心叫做椭圆的中心。YXOP（x，y）P1（-x，y）P2（-x，-y）二、椭圆的对称性）（中，关于原点对称的是下列方程所表示的曲线49.54.04.2.222222yxDxyxCxyByxA练习2.D三、椭圆的顶点22221(0)£¬xyabab在中令x=0，得y=？，说明椭圆与y轴的交点（），令y=0，得x=？,说明椭圆与x轴的交点（）*顶点：椭圆与它的对称轴的四个交点，叫做椭圆的顶点。oxyB1(0,b)B2(0,-b)A1A2(a,0)0,±b±a,0*长轴、短轴：线段A1A2、B1B2分别叫做椭圆的长轴和短轴。a、b分别叫做椭圆的长半轴长和短半轴长。14922yx标及长轴和短轴长。口答下列椭圆的顶点坐练习3.46)2,0()2,0()0,3()0,3(，短轴长是长轴长是顶点是：、、、练习4.画出下列椭圆的草图1162522yx142522yx（1）（2）B1123-1-2-3-44yA1A2B212345-1-5-2-3-4x0123-1-2-3-44yB2A2B1A112345-1-5-2-3-4x0思考：圆的形状都是相同的，而椭圆却有些比较“扁”，有些比较“圆”，用什么样的量来刻画椭圆“扁”的程度呢？四、椭圆的离心率ace离心率：椭圆的焦距与长轴长的比叫做椭圆的离心率。[1]离心率的取值范围：[2]离心率对椭圆形状的影响：0|F1F2|)(c,0)、(c,0)(0,c)、(0,c)(a,0)、(0,b)|x|a|y|b|x|b|y|a关于x轴、y轴、原点对称(b,0)、(0,a)ace一个框，四个点，注意光滑和圆扁，莫忘对称要体现例1求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点坐标。解：把已知方程化成标准方程1452222yx31625,4,5cba椭圆的长轴长是:离心率:6.053ace焦点坐标是:)0,3(),0,3(21FF四个顶点坐标是:)4,0(),4,0(),0,5(),0,5(2121BBAA椭圆的短轴长是:2a=102b=8题型一椭圆的简单几何性质巩固练习：1.若点P（x，y）在椭圆192522yx上，则点P（x，y）横坐标x的取值范围？3.说出椭圆的长轴长，短轴长，顶点和焦点坐标16422yx2.若点P（2，4）在椭圆上，下列是椭圆上的点有（1）P（-2，4）（2）P（-4，2）（3）P（-2，-4）（4）P（2，-4）)0(12222babyax4.已知椭圆的离心率，求的值19822ykx21ek题型二由椭圆的几何性质求方程【例2】求满足下列各条件的椭圆的标准方程.(1)已知椭圆的中心在原点，焦点在y轴上，其离心率为12，焦距为8；(2)已知椭圆的离心率为e...