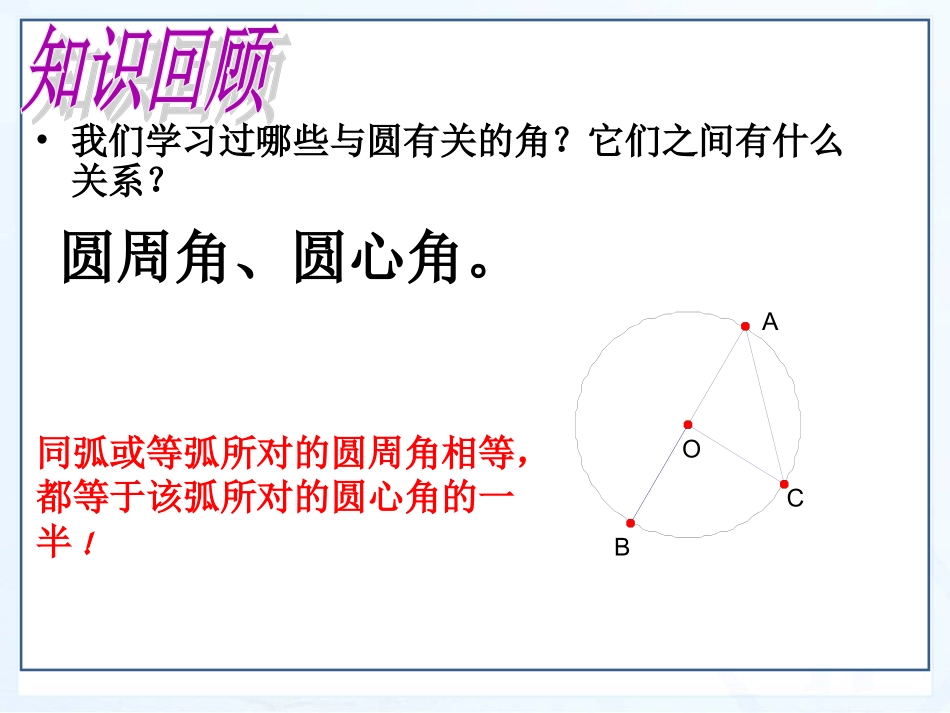
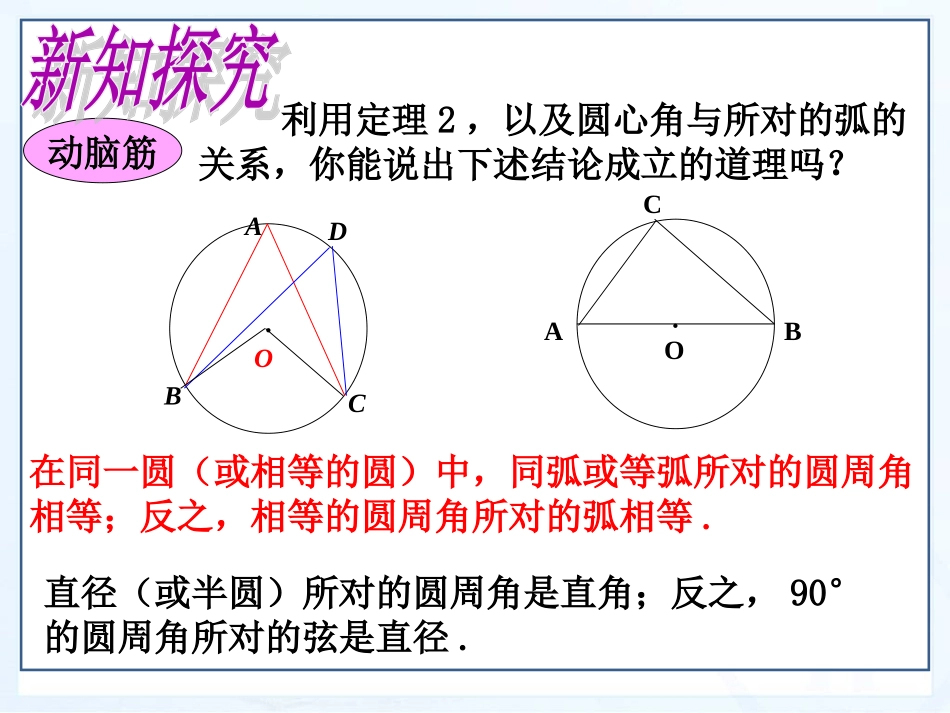
第二章圆•我们学习过哪些与圆有关的角?它们之间有什么关系?圆周角、圆心角。同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半!OCBA动脑筋利用定理2,以及圆心角与所对的弧的关系,你能说出下述结论成立的道理吗?直径(或半圆)所对的圆周角是直角;反之,90°的圆周角所对的弦是直径.A·OBCD·ABCO在同一圆(或相等的圆)中,同弧或等弧所对的圆周角相等;反之,相等的圆周角所对的弧相等.例3.如图,AB是⊙O的直径,点D在圆O上∠ABC=60°,求∠CDB的度数?EODCBA例题例题解:∵AB是⊙O的直径又∵∠CDB与∠CDB都是BC所对的圆周角∴∠ACB=90°又∠ABC=60°∴∠CAB=30°⌒∴∠CDB=∠CAB=30°11、如图、如图(1)(1),△,△ABCABC叫⊙叫⊙OO的的__________三角形,⊙三角形,⊙OO叫△叫△ABCABC的的________圆。圆。22、、如上图如上图(1),(1),若弧若弧BCBC的度数为的度数为10010000,,则∠则∠BOC=__BOC=__,A=∠,A=∠____33、如图、如图(2)(2)四边形四边形ABCDABCD中中,B∠,B∠与∠与∠11互补互补,AD,AD的延长线与的延长线与DCDC所夹∠所夹∠2=602=6000,,则∠则∠1=___1=___,B=___∠,B=___∠..4.4.判断判断::圆上任意两点之间分圆周为两条弧圆上任意两点之间分圆周为两条弧,,这两条弧的度数和为这两条弧的度数和为36036000()()图图11图图22ABCOEDCBA21内接外接100°50°120°60°√若一个四边形各顶点都在同一个圆上,那么,这个四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆。OACDBCODBA如图:圆内接四边形ABCD中,∵弧BCD和弧BAD所对的圆心角的和是周角∴∠A+∠C=180°同理∠B+∠D=180°圆的内接四边形的对角互补。四边形中两组对角∠A与∠C,∠B与∠D有什么关系?如图,四边形ABCD为⊙O圆的内接四边形∠∠BOD=100°BOD=100°求∠求∠BADBAD及∠及∠BCDBCD的度数。的度数。解:∵圆心角∠BOD与圆周角∠BAD所对的弧为BD∠∠BOD=100°BOD=100°⌒∴∠BAD=∠BOD∠BOD=100°=50°=100°=50°1212∵∠∠BCD+∠BAD=180°BCD+∠BAD=180°∴∠BCD=180°-∠BAD=130°180°-∠BAD=130°AODBC(1)四边形ABCD内接于⊙O,则∠A+∠C=__,∠B+∠ADC=_____;若∠B=800,则∠ADC=______∠CDE=______(图1)(2)四边形ABCD内接于⊙O,∠AOC=1000则∠B=______∠D=_____(图2)(3)四边形ABCD内接于⊙O,∠A:∠C=1:3,则∠A=_____,EDBAC80DBACO100180°180°100°50°45°填空130°80°例1.如图,在⊙O中,△ABC是等边三角形,AD是直径,则∠ADB=°,DAB=∠°.ODCBA第1题典型例题典型例题例2.如图,AB是⊙O的直径,若AB=AC,求证:BD=CDODCBA第2题例1.如图,AB是⊙O的直径,弦CD与AB相交于点E,ACD=60°,∠ADC=50°,求∠CEB的度数.EODCBAEODCBA典型例题典型例题例2.如图,△ABC的顶点都在⊙O上,AD是△ABC的高,AE是⊙O的直径.ABE△与△ACD相似吗?为什么?EODCBAFEODCBA例3.如图,A、B、E、C四点都在⊙O上,AD是△ABC的高,∠CAD=EAB,AE∠是⊙O的直径吗?为什么?ABECDO延伸拓展延伸拓展1.如图,AB是⊙O的直径,∠A=10°,则∠ABC=___.2.如图,AB是⊙O的直径,CD是弦,∠ACD=40则∠BCD=_______,BOD=_______.∠巩固练习巩固练习3.如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状:__________。4.如图,AB是⊙O的直径,AC是弦,∠BAC=30°,则AC的度数是()A.30°B.60°C.90°D.120°通过本课的学习,你又有什么收获?1.直径(或半圆)所对的圆周角是直角;2.90°的圆周角所对的弦是直径.3.在同圆或等圆中,相等的圆周角所对的弧相等4.圆内接四边形和四边形的外接圆。圆的内接四边形的对角互补。人生在勤,不索何获?——张衡