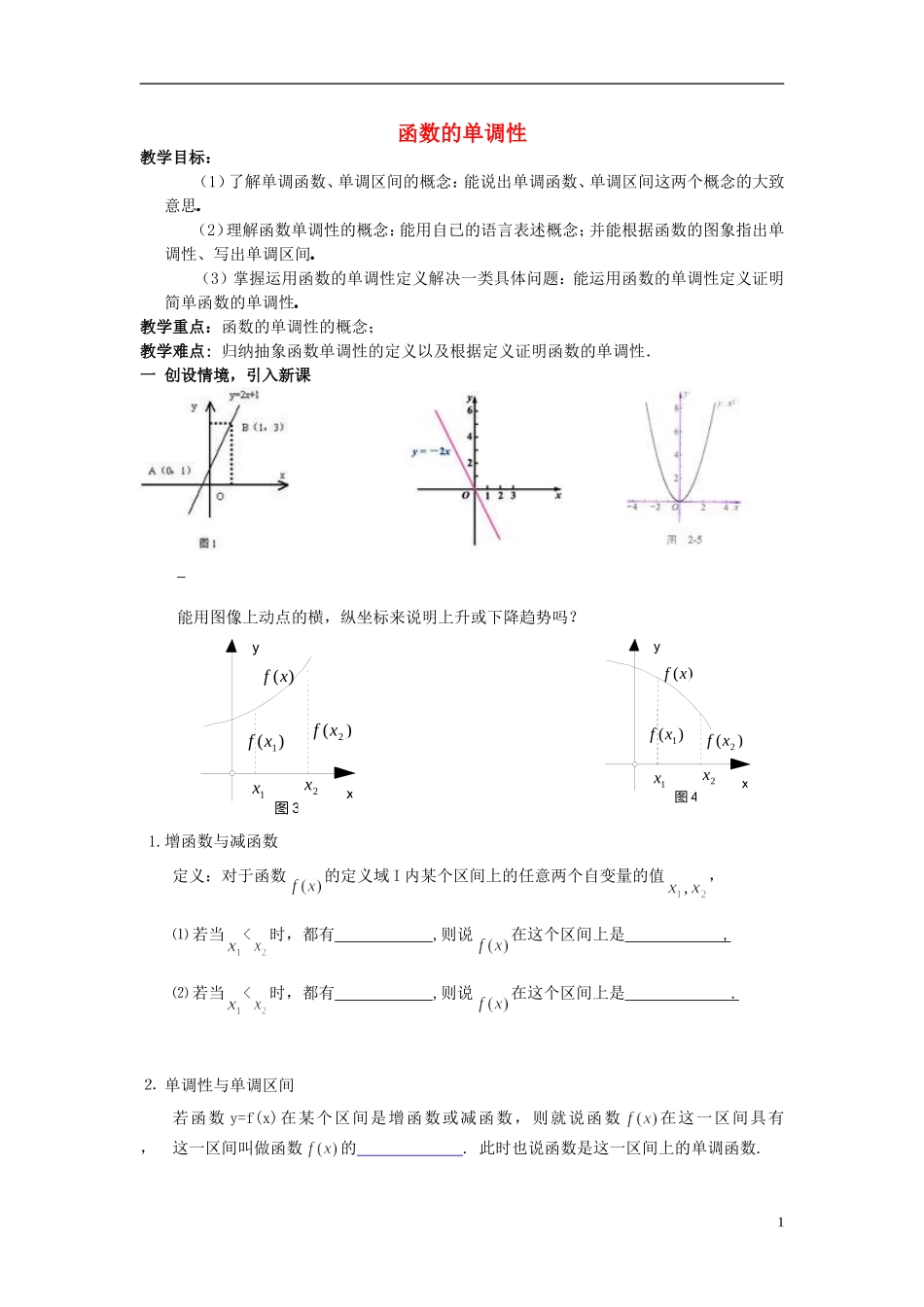
1x2x)(1xf)(2xf)(xf3图yx1x2x)(1xf)(2xf)(xf4图yx函数的单调性教学目标:(1)了解单调函数、单调区间的概念:能说出单调函数、单调区间这两个概念的大致意思奎屯王新敞新疆(2)理解函数单调性的概念:能用自已的语言表述概念;并能根据函数的图象指出单调性、写出单调区间奎屯王新敞新疆(3)掌握运用函数的单调性定义解决一类具体问题:能运用函数的单调性定义证明简单函数的单调性奎屯王新敞新疆教学重点:函数的单调性的概念;教学难点:归纳抽象函数单调性的定义以及根据定义证明函数的单调性.一创设情境,引入新课能用图像上动点的横,纵坐标来说明上升或下降趋势吗?1.增函数与减函数定义:对于函数的定义域I内某个区间上的任意两个自变量的值,⑴若当<时,都有,则说在这个区间上是,⑵若当<时,都有,则说在这个区间上是.⒉单调性与单调区间若函数y=f(x)在某个区间是增函数或减函数,则就说函数在这一区间具有,这一区间叫做函数的.此时也说函数是这一区间上的单调函数.1注意:(1)(2)(3)二、知识应用:典型例1如图是定义在闭区间[-5,5]上的函数的图象,根据图象说出的单调区间,以及在每一单调区间上,函数是增函数还是减函数.方法小结:小试身手:判断函数的单调性,并写出函数的单调区间.典型例2用定义法证明函数在R上是增函数.方法小结:用定义法证明函数单调性的一般步骤123452531-2-5xOy→→→→探究:画出函数的图像,并探究它在(0,+)和定义域上的单调性.三.达标练习1.判断下列说法的正误(正确的打“√”,错误的打“×”)(1)定义在R上的函数满足,则是R上的增函数()(2)定义在R上的函数满足,则在R上不是减函数()(3)定义在R上的函数在区间上是增函数,则在R上是增函数()(4)定义在R上的函数在区间上是增函数,在区间(0,+∞)上也是增函数,则在R上是增函数()2.函数=12x,x[-1,2]的单调性()(A)减函数(B)增函数(C)先减后增(D)先增后减3.函数y=-x2的单调增区间()(A)(-∞,0](B)[0,+∞)(C)(0,-∞)(D)(-∞,+∞)4.若(a,b)是函数的单调增区间,,(a,b),且<,则有()(A)f(x1)<f()(B)f(x1)=()(C)(D)以上都可能5.下列说法正确的是()(A)若存在,,且<,使得,则为增函数(B)若存在无数多对,当<时,有,则为增函数(C)若分别在开区间(a,b),(c,d)上是增函数,则在上是增函数3(D)若在区间(a,b)上是增函数,,,则<6.判断并证明函数在上上的单调性。四.课堂小结(1)(2)(3)五布置作业课本39页习题1.3A组第1,2题课后探究:研究函数的单调性.4