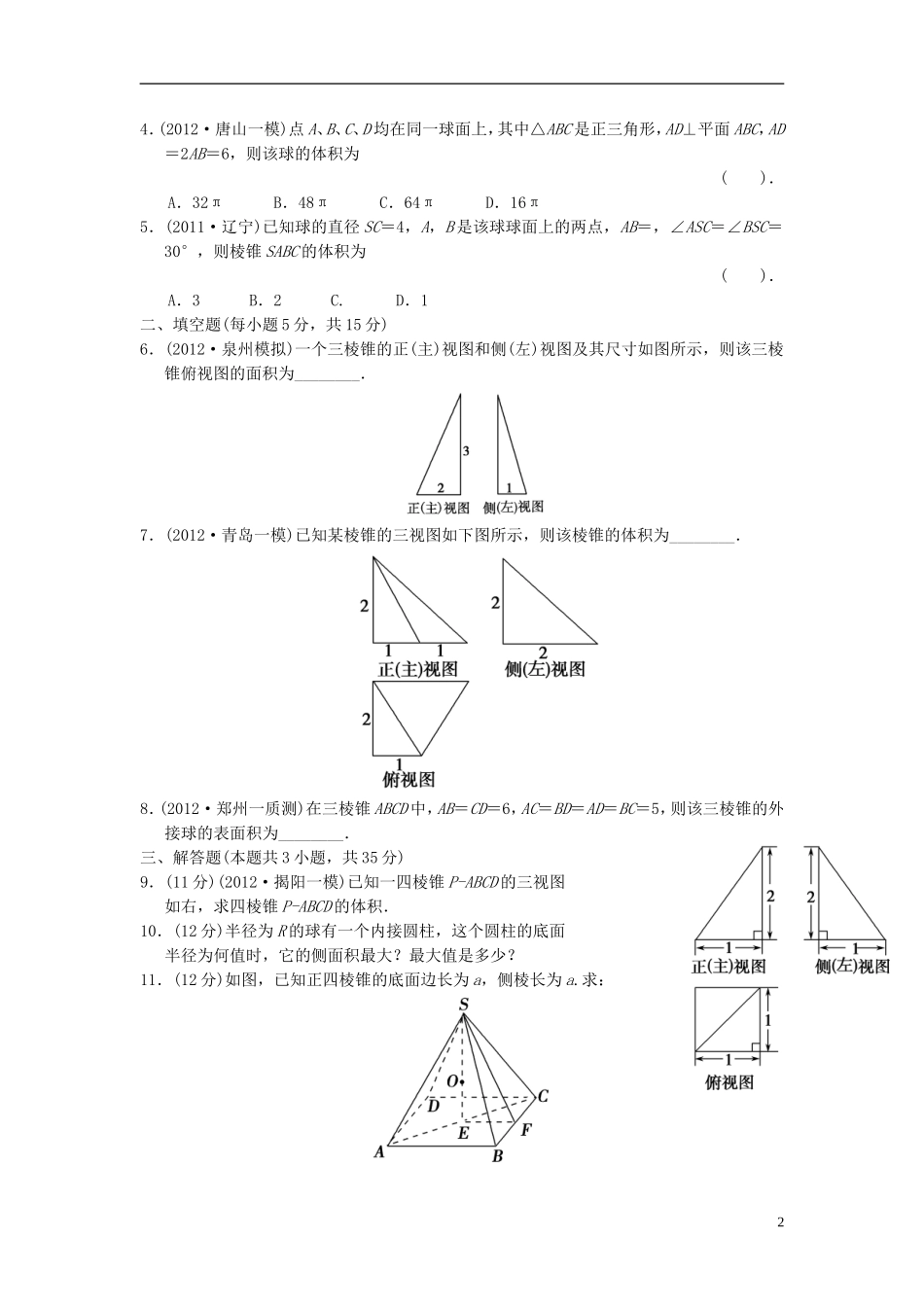
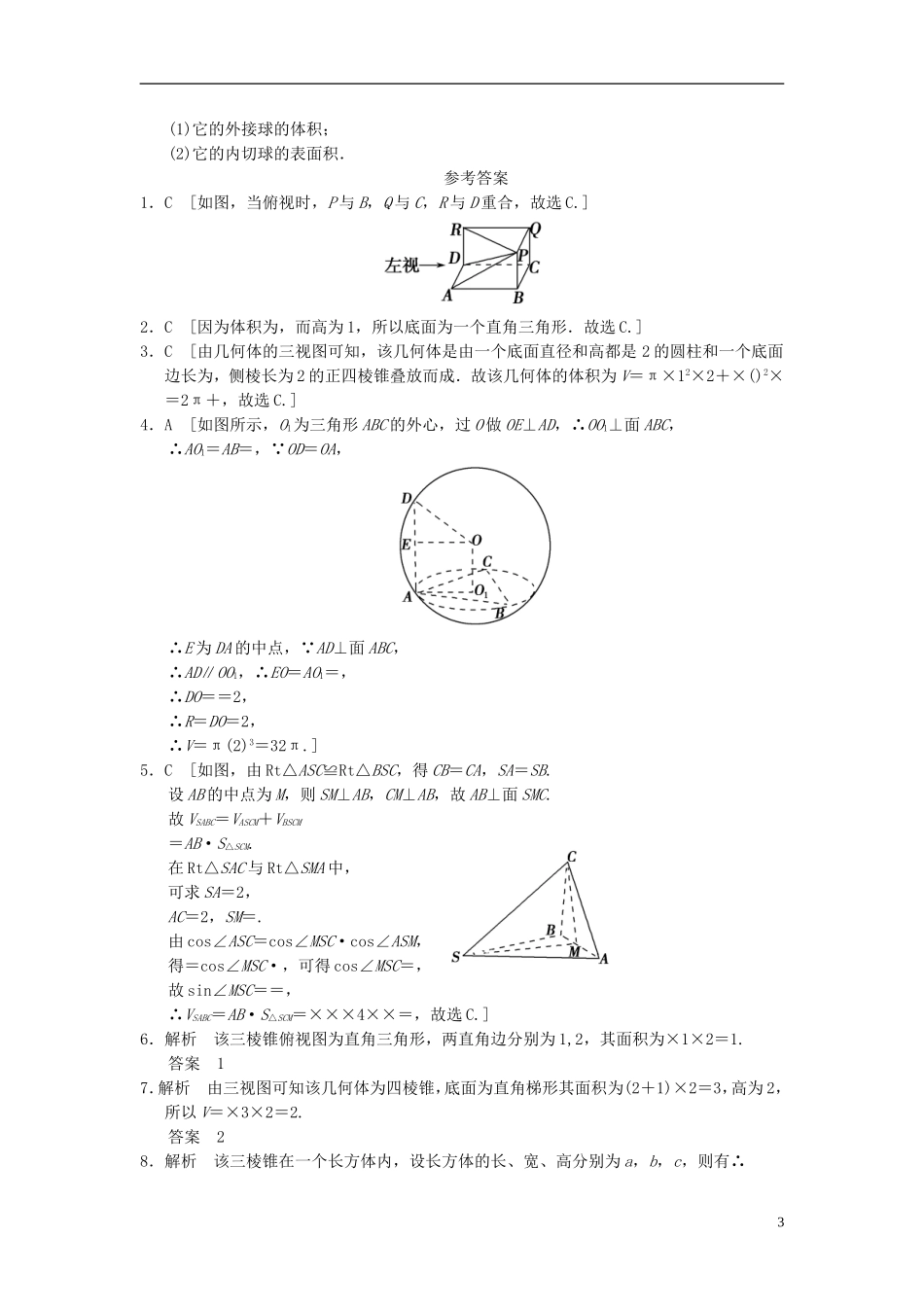
训练12三视图及空间几何体的计算问题(时间:45分钟满分:75分)一、选择题(每小题5分,共25分)1.(2012·石家庄质检)将长方体截去一个四棱锥后,得到的几何体的直观图如下图所示,则该几何体的俯视图为().2.如图,某几何体的正(主)视图与侧(左)视图都是边长为1的正方形,且体积为,则该几何体的俯视图可以是().3.一空间几何体的三视图如图所示,则该几何体的体积为().A.2π+2B.4π+2C.2π+D.4π+14.(2012·唐山一模)点A、B、C、D均在同一球面上,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6,则该球的体积为().A.32πB.48πC.64πD.16π5.(2011·辽宁)已知球的直径SC=4,A,B是该球球面上的两点,AB=,∠ASC=∠BSC=30°,则棱锥SABC的体积为().A.3B.2C.D.1二、填空题(每小题5分,共15分)6.(2012·泉州模拟)一个三棱锥的正(主)视图和侧(左)视图及其尺寸如图所示,则该三棱锥俯视图的面积为________.7.(2012·青岛一模)已知某棱锥的三视图如下图所示,则该棱锥的体积为________.8.(2012·郑州一质测)在三棱锥ABCD中,AB=CD=6,AC=BD=AD=BC=5,则该三棱锥的外接球的表面积为________.三、解答题(本题共3小题,共35分)9.(11分)(2012·揭阳一模)已知一四棱锥P-ABCD的三视图如右,求四棱锥P-ABCD的体积.10.(12分)半径为R的球有一个内接圆柱,这个圆柱的底面半径为何值时,它的侧面积最大?最大值是多少?11.(12分)如图,已知正四棱锥的底面边长为a,侧棱长为a.求:2(1)它的外接球的体积;(2)它的内切球的表面积.参考答案1.C[如图,当俯视时,P与B,Q与C,R与D重合,故选C.]2.C[因为体积为,而高为1,所以底面为一个直角三角形.故选C.]3.C[由几何体的三视图可知,该几何体是由一个底面直径和高都是2的圆柱和一个底面边长为,侧棱长为2的正四棱锥叠放而成.故该几何体的体积为V=π×12×2+×()2×=2π+,故选C.]4.A[如图所示,O1为三角形ABC的外心,过O做OE⊥AD,∴OO1⊥面ABC,∴AO1=AB=,∵OD=OA,∴E为DA的中点,∵AD⊥面ABC,∴AD∥OO1,∴EO=AO1=,∴DO==2,∴R=DO=2,∴V=π(2)3=32π.]5.C[如图,由Rt△ASC≌Rt△BSC,得CB=CA,SA=SB.设AB的中点为M,则SM⊥AB,CM⊥AB,故AB⊥面SMC.故VSABC=VASCM+VBSCM=AB·S△SCM.在Rt△SAC与Rt△SMA中,可求SA=2,AC=2,SM=.由cos∠ASC=cos∠MSC·cos∠ASM,得=cos∠MSC·,可得cos∠MSC=,故sin∠MSC==,∴VSABC=AB·S△SCM=×××4××=,故选C.]6.解析该三棱锥俯视图为直角三角形,两直角边分别为1,2,其面积为×1×2=1.答案17.解析由三视图可知该几何体为四棱锥,底面为直角梯形其面积为(2+1)×2=3,高为2,所以V=×3×2=2.答案28.解析该三棱锥在一个长方体内,设长方体的长、宽、高分别为a,b,c,则有∴3外接球的半径为=,∴S=4π×2=43π.答案43π9.解由该四棱锥的三视图可知,该四棱锥PABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,且PC=2,所以VPABCD=S四边形ABCD·PC=.10.解取圆柱的一个轴截面ABCD,则⊙O为球的一个大圆.设圆柱的半径为r,高为h,侧面积为S.连接OB,作OH⊥AB交AB于H.在Rt△OBH中,有2=R2-r2,即h=2.所以S=2πrh=2πr·2=4πr·,所以S2=16π2r2(R2-r2)=-16π2(r2)2+16π2R2r2.因为这是一个关于r2的二次函数,所以,当r2=-=,即r=R时,S有最大值,最大值为4π·R×=2πR2.故当这个圆柱的底面半径为R时,它的侧面积最大,最大值是2πR2.11.解(1)设外接球的半径为R,球心为O,则OA=OC=OS,所以O为△SAC的外心,即△SAC的外接圆半径就是球的半径.因为AB=BC=a,所以AC=a.所以△SAC为正三角形.由正弦定理得,2R===a,因此R=a,则V外接球=πR3=πa3.(2)设内切球的半径为r.作SE⊥底面于E,作SF⊥BC于F,连接EF.则有SF===a,所以S△SBC=BC·SF=a×a=a2,所以S棱锥全=4S△SBC+S底=(+1)a2.又SE===a,所以V棱锥=S底×h=a2×a=a3.所以r===a,所以S球=4πr2=πa2.4